C语言空间直角坐标与大地坐标的相互转换实验报告

C语言空间直角坐标与大地坐标的相互转换实验报告

---

源代码附文末或见Github:⬇️
直角坐标与大地坐标的相互转化

branch:

• master: 正常读取输入。
• file_read: 从csv文件获取输入。

一、实验名称：空间直角坐标与大地坐标的相互转换

二、实验目的与要求

三、实验内容

1. 已知某点的空间直角坐标（X、Y、Z）， X = 1546823.34，Y = -3879765.13，Z = 4804185.05，椭球参数a= 6378137m，b= 6356752.3141m，采用下式将其转换为大地坐标（L、B）
   

2. 根据1所求的大地坐标（L、B）及大地高H及相同的椭球参数将其转化为空间直角坐标（X、Y、Z），计算式为：

四、试验设备与环境

五、实验步骤

1 && 2 分析和算法设计

公理1 :由于 $LBH$ 和 $XYZ$ 是相同物理量在相同参考系下的不同表示方法，因此在空间直角坐标系上的某点$(XYZ)$，有且只有一个$LBH$在大地坐标系与之对应。

推论1 只要$XYZ$确定，$LBH$的值就只与$XYZ$的取值有关，而与任何其他变量无关。

下面展开讨论：

由方程可知，虽然 $L$ 可以直接求解，但求 $B$ 的方程中，包含 $B$ 本身，为了验证方程(2)是否可以求解，我们先将方程(2)化简：
$$\begin{array}{c}B=\arctan \frac{Z+N{e}^2\sin B}{\sqrt{X^2+Y^2}}\\ \tan B=\frac{Z+N{e}^2\sin B}{\sqrt{X^2+Y^2}}\end{array}\text{\hspace{1em}(2)}$$
为了方便化简，我们令
$$\sqrt{X^2+Y^2}=R\text{\hspace{1em}(3)}$$
又由于
$$N=\frac{a}{\sqrt{1-e^2{\sin }^{2}B}}\text{\hspace{1em}(4)}$$
将（4）、（3）带入(2)中
$$\begin{array}{cc}\tan B& =\frac{Z}{R}+\frac{e^2}{R}NsinB\\ & =\frac{Z}{R}+\frac{e^2}{R}\frac{\sin B}{\sqrt{1-e^2{\sin }^{2}B}}\\ & =\frac{Z}{R}+\frac{a{e}^2}{R}\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}\end{array}\text{\hspace{1em}(5)}$$
由 推论1 可知，上式中 $\frac{Z}{R}$ 与 $\frac{a{e}^2}{R}$ 与 $B$ 的值无关，为了方便表示，我们令
$$\frac{Z}{R}=C,\frac{a{e}^2}{R}=K.$$

上式化简为：

$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(6*)}$$

在上式中，由于 $\frac{\tan B}{\sin B}=\cos B$ 不为常量，故无法找到一组$k_1,k_2\in R$ 满足$k_1\tan B+k_2\sin B=0$。因此上式左右两端含有变量 $B$ 的因子是非线性相关的，所以不可以直接通过方程求解。

由此，为得到$B$ 的值，必须通过其他方式求解。

利用计算机程序可以通过不断猜测 $B$ 的值，带入(6)式中，如果(6)左右两端的值足够接近，且由 推论1, 此时猜测到的值 $B_{猜}$ 必然也会接近实际的值$B_{实}$。

我们将上述求 $B$ 的方法称为遍历法，接下来我们设计遍历法的算法。

遍历法

由题设条件，可知$B\in (-\frac{\pi }{2},\frac{\pi }{2})$。

• 一个可执行的算法必须由有限步构成。

但是可能出现的 $B$ 的值确是无限的，为此，我们将 $B$ 进行离散化 ，即每隔很小的值 $\delta (delta)$ ，取一个新的值$B$。

为了方便表示，我们设计损失函数$Loss$用来计算方程左右两端的差值。
$$Loss(B)=\tan B-K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(7)}$$
当函数Loss的值很小时，则认为此时的$B$达到了目标值$B_{实}$。

用数学语言可以描述为：

若取一个足够小的 $\epsilon >0$，

对于
$$B_0=-\frac{\pi }{2}+k\delta ,且(k\in N^{\ast })B_0<\frac{\pi }{2}$$
时，如果满足
$$|Loss(B_0)|<\epsilon$$
则认为 $B=B_0$。

---

梯度下降法

使用遍历法​求解时，往往会由于需要遍历的变量的数量太多，导致程序的运行时间太长，难以得到正确的结果。当我们遍历时，只是盲目的遍历，我们并不知道到底经过多少个 $\delta$ 后，能够使$Loss$函数的绝对值变小。这是因为，我们只用 $Loss$ 函数的值与0比较，这样的比较获得的信息量是十分少的，为了从 $Loss$ 函数中获取更多信息，我们可以考虑将 $Loss$ 函数的绝对值进行求导，将其导函数记为$Los{s}^{\prime }$

我们的目标是使 $Loss$ 函数的值趋近于0，对于一个点$(B,Loss(B))$ ，如果$Loss(B)>0$，我们应该调整 $B$ 的值，使得$Loss(B)$减少，相反，如果$Loss(B)<0$， 我们应该调整$B$的值，使$Loss(B)$增加。

即：

• $Loss(B)>0$, $B$ 向 $Los{s}^{\prime }(B)<0$的方向移动。
• $Loss(B)<0,B$ 向 $Los{s}^{\prime }(B)>0$ 的方向移动。

以点$X=-2758534,Y=-4132154,Z=3986124$为例，

绘制出$Loss$函数的图像：

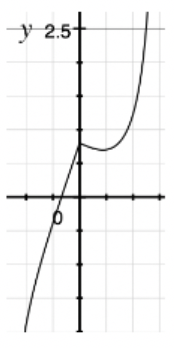
发现$Loss$函数并不是简单的单调函数，用上述算法有可能达到一个使$Loss(B)$为0的点，也有可能达到函数的一个极值点，并不是在所有情况下都能符合条件。

---

二分法

虽然梯度下降法无法实现，但这给我们进一步实现程序提供了思路，即让 $B$ 的取值变得更加具有方向性。

由于当$B\to -\frac{\pi }{2}$ 时，
$$Loss(B)\to -\infty$$
当$B\to \frac{\pi }{2}$时，
$$Loss(B)\to +\infty$$
又由推论2可知，在区间$(-\frac{\pi }{2},\frac{\pi }{2}）$内，$Loss(B)$有且只有一个一个零点。可以很容易想到二分法的求解方式：

• $LoopStart:$
• $mid=\frac{right+left}{2}$
• $ifLoss(mid)>\epsilon ,left=mid$
• $elseifLoss(mid)<-\epsilon ,right=mid$
• $elseB=mid$
• $:LoopEnd$

---

迭代法

由于式(6)
$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C\text{\hspace{1em}(6*)}$$
如果我们令方程左边的$B=B_{n+1}$ 方程右边的 $B=B_n$，就可以得到一个关于$B$ 的迭代方程。
$$B_{n+1}=\arctan \left(K\frac{1}{\sqrt{\frac{1}{{\sin }^2{B}_n}}-e^2}+C\right)\text{\hspace{1em}(8*)}$$
我们称上面的递推式为函数$Forward(B)$。

以点$X=-2758534,Y=-4132154,Z=3986124$为例，

绘制出$Forward$函数的图像：

上图中粗线为$Forward$函数，虚线为直线 $B_{n+1}=B_n$。

设曲线$Forward$ 与 直线$B_{n+1}=B_n$的交点为 $A$ ，$A$的横坐标为$x_0$，很显然 $A$是函数$Forward$ 的一阶不动点。由递推函数的性质可知，

• 当$B_n<x_0$ 时， $B_{n+1}>B_n$

• 当$B_n>x_0$时，$B_{n+1}<B_n$

• 当$B_n=x_0$时，$B_{n+1}=B_n$

  因此如果迭代次数无穷大，那么$B_n$的值会无限接近于$x_0$或等于$x_0$。

  我们用$Python$模拟一下迭代过程：

  from math import *
  import matplotlib.pyplot as plt
  
  a = 6378137
  b = 6356752
  e = sqrt((a * a - b * b) / (a * a))
  X = -2758534
  Y = -4132154
  Z = 3986124
  R = sqrt(X * X + Y * Y)
  K = a * e * e / R
  C = Z / R
  x = []
  y = []
  
  
  def forWard(x):
      N = a / sqrt(1 - e * e * sin(B) * sin(B))
      tmp = sqrt(1/(sin(x) * sin(x)) - e * e)
      return atan(K / tmp + 0.1) + C
  
  
  B = C
  times = 100
  t = 0
  while True:
      t += 1
      nextB = forWard(B)
      #plt.plot(t, nextB, '+')
      B = nextB
      if t >= times:
          break
      x.append(t)
      y.append(B)
  plt.xlabel("times")
  plt.ylabel("B")
  plt.plot(x, y)
  plt.show()
  

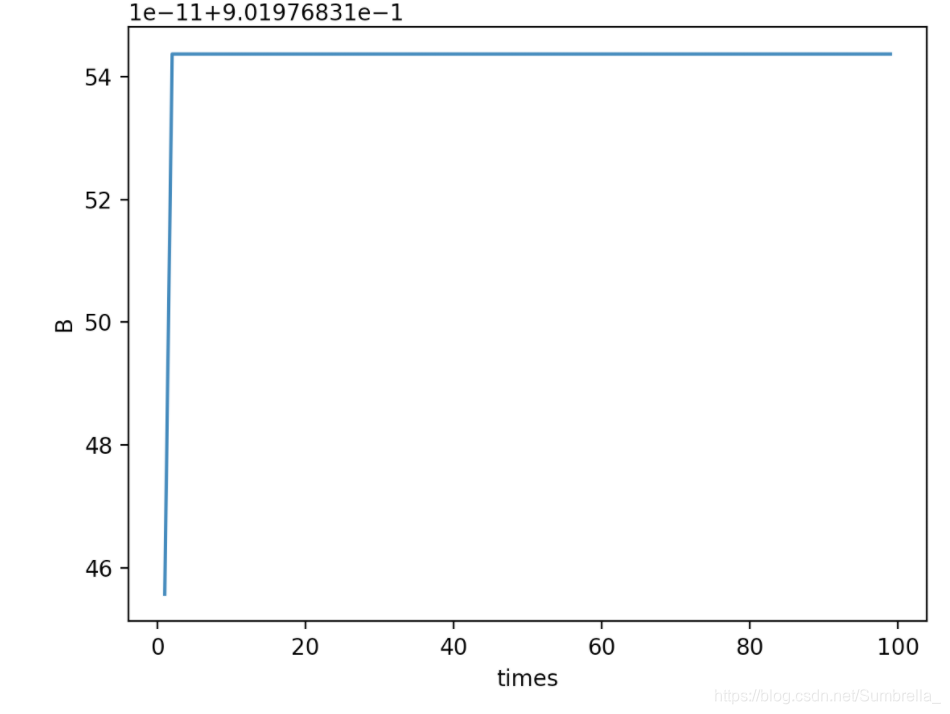
理论和实践都告诉我们，使用迭代公式计算时，$B$ 会趋近于某一个特殊的值$x_0$。

下证：该$x_0$就是我们的目标值$B_{实}$

​ 当 $B=x_0$时，由于 $x_0$是$Forward$ 函数的一阶不动点，故有
$$\tan B=K\frac{1}{\sqrt{\frac{1}{{\sin }^{2}B}-e^2}}+C$$
​ 将上式带入$Loss$函数中，可以得到 $Loss(B)=0$，又由推论1知这样的$B$是唯一的，因此$B=x_0$ 就是所求值。

​ 证毕。

(上述证明其实显而易见，用迭代法的关键是证明一阶不动点存在， 但是该证明过程较为复杂，我们可以在物理领域内使用反证法：如果不存在一阶不动点，那么函数$Loss$就没有解，这与实际情况不符，故一定存在一阶不动点)。

第二小问直接带入公式计算。

3流程图

遍历法：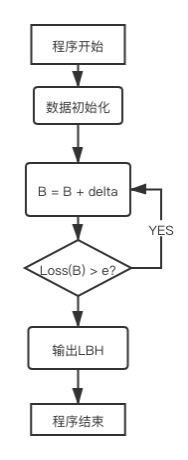

二分法：

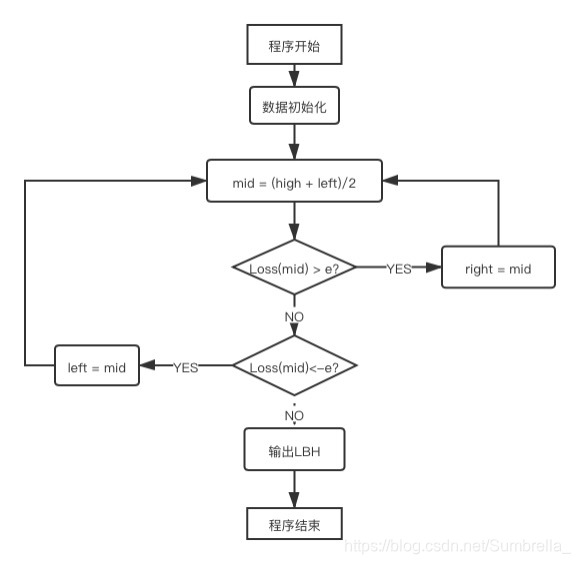
迭代法：

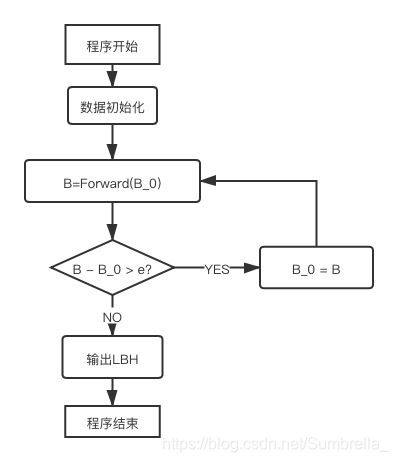
4、 程序代码

本部分只使用迭代法完成代码。

//
//  main.cpp
//  ChangePosition
//
//  Created by Sumbrella on 2020/4/28.
//  Copyright © 2020 Sumbrella All rights reserved.
//
# include <stdio.h>
# include <math.h>

typedef long long ll;

const ll a = 6378137;
const ll b = 6356752;
const double epslion = 1e-15;
double e, R, K, C;

// 配置需要使用的中间参数。
void configure(double X, double Y, double Z)
{
    e = sqrt((a * a - b * b) / (a * a));
    R = sqrt(X * X + Y * Y);
    K = a * e * e / R;
    C = Z / R;
}

// 迭代法迭代一次
double Forward(double B)
{
    double tmp = sqrt(1 / (sin(B) * sin (B)) - e * e );
    return atan(K / tmp + C);
}


void inputXYZ(double *X,double *Y, double *Z)
{
    printf("请输入X，Y，Z的值>>>（空格隔开）");
    scanf("%lf %lf %lf", X, Y, Z);
}


void getLBH(double X, double Y, double Z, double *pN, double *pL, double *pB, double *pH)
{
    double B = C;                   // 让B的初始值为C
    while (1)
    {
        double nB = Forward(B);
        if (nB - B < epslion && nB - B > -epslion)
            break;
        B = nB;
    }
    double N = a / sqrt(1 - e * e * sin(B) * sin(B));
    double L = atan2(Y, X);
    double H = R / cos(B) - N;
    
    *pN = N; *pL = L; *pB = B; *pH = H;
}


void showLBH(double L, double B, double H)
{
    printf("转换得到的大地坐标：\n");
    printf("L = %.3f, B = %.3f, H = %.3f\n", L, B, H);
}


void showXYZ(double N, double L, double B, double H)
{
    double X = (N + H) * cos(B) * cos(L);
    double Y = (N + H) * cos(B) * sin(L);
    double Z = (N * (1 - e * e) + H) * sin(B);
    printf("转换后得到的空间坐标：\n");
    // printf("N = %.6f", N);
    printf("X = %.6f, Y = %.6f, Z = %.6f\n", X, Y, Z);
}

int main()
{
    double X, Y, Z;
    double N, L, B, H;                // 定义变量

    inputXYZ(&X, &Y, &Z);             // 获取XYZ的值

    configure(X, Y, Z);               // 配置参数

    getLBH(X, Y, Z, &N, &L, &B, &H);  // 计算LBH的值

    showLBH(L, B, H);                 // 输出LBH的值

    showXYZ(N, L, B, H);              // 输出计算得到的XYZ的值

    
    return 0;
}

5、 主要函数和变量说明

主要函数说明见上图。
变量和常量说明：
（X，Y，Z）、（L，B，H）分别对应直角坐标和大地坐标下的坐标值。
C = Z / R， K = ae^2 / R。

6、 程序运行结果

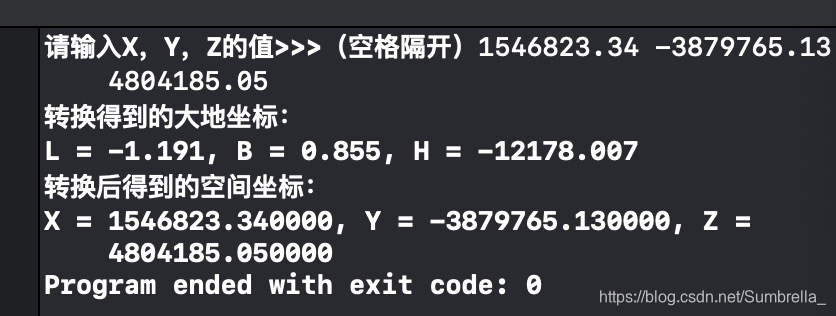
转换后得到的坐标与原始数据完全一致，认为程序通过。