机器学习工程实践——模型复杂度度量

小老弟来喽

已于 2023-07-23 18:40:49 修改

阅读量853

点赞数

分类专栏：机器学习文章标签：机器学习 python 人工智能

于 2023-07-23 18:32:48 首次发布

本文链接：https://blog.csdn.net/T940842933/article/details/131876860

版权

机器学习专栏收录该内容

10 篇文章

订阅专栏

1.1 偏差与方差

偏差——方差分解是解释学习模型泛化能力的一种重要工具

泛化误差 = 错误率( $error$ ) = 偏差 + 方差 + 噪声

数学公式定义如下：

对训练集 $T$ 中的测试样本 $x$ ，设 $y$ 为 $x$ 的真实结果， $\hat{y}$ 为 $x$ 的预测结果，预测结果与真实结果之间的误差为 $y-\hat{y}=\epsilon$ ， $f_T(x)$ 为在训练集 $T$ 上学得模型 $f$ 对 $x$ 的预测输出，则：

$\bullet$ 噪声： $var(\epsilon )=E[(y-\hat{y})^2]$

噪声 $var(\epsilon )$ 表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度

$\bullet$ 模型在训练集 $T$ 上的预测期望： $\bar{f}(x)=E(f_T(x))$

预测期望 $\bar{f}(x)$ 是针对不同的训练集 $T$ ，模型 $f$ 对 $x$ 的预测值取其期望

$\bullet$ 模型在训练集 $T$ 上的预测方差： $var(x)=E[(f_T(x)-\bar{f}(x))^2]$

方差 $var(x)$ 度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响

$\bullet$ 模型在训练集 $T$ 上的预测偏差： $bias^2=E[(y-\bar{f}(x))^2]$

偏差 $bias^2$ 度量了学习算法的预测期望 $\bar{f}(x)$ 与真实结果 $y$ 的偏离程度，即刻画了算法本身的拟合能力

由上可得模型在训练集 $T$ 上泛化误差期望为

$E[(f_T(x)-\hat{y})^2] \\\\=E[(f_T(x)-\bar{f}(x) +\bar{f}(x) -\hat{y})^2] \\\\=E[ (f_T(x)-\bar{f}(x) )^2+(\bar{f}(x) -\hat{y})^2 +2(f_T(x)-\bar{f}(x) )(\bar{f}(x) -\hat{y})] \\\\=E[(f_T(x)-\bar{f}(x) )^2]+E[(\bar{f}(x) -\hat{y})^2]+2E[(f_T(x)-\bar{f}(x) )(\bar{f}(x) -\hat{y})] \\\\=var(x)+E[(\bar{f}(x) - y + y -\hat{y})^2] \\\\=var(x)+E[(\bar{f}(x) - y)^2]+E[(y -\hat{y})^2]+2E[(\bar{f}(x) - y)(y -\hat{y})] \\\\=var(x)+bias^2+var(\epsilon )$

当预测结果与真实结果无限接近时，即噪声为0，则误差 $\epsilon=y-\hat{y}\approx 0$ ，上述推导过程中

$2E[(f_T(x)-\bar{f}(x) )(\bar{f}(x) -\hat{y})]$ 、 $E[(\bar{f}(x) - y)(y -\hat{y})]$ 分别为 0

偏差——方差分解说明，泛化性能是由所用模型的能力、数据的充分性及学习任务本身的难度共同决定的

给定学习任务，为了取得好的预测性能，则需使模型偏差较小；为了能够充分利用数据，则需使方差较小，如下图所示（懒得做图了，嘻嘻）

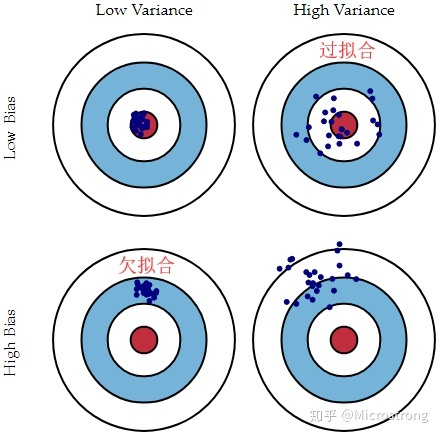
偏差——方差分解说明

$\bullet$ 圆心为完美预测的模型，点代表某个模型的学习结果（离靶心越远，准确率越低）

$\bullet$ Low Bias表示离圆心近，High Bias表示离圆心远

$\bullet$ LowVariance表示学习结果集中，High Variance表示学习结果分散

一般来说，偏差和方差是有冲突的，偏差随着模型复杂度的增加而降低，而方差随着模型复杂度的增加而增加，如图所示（依然不想画图，O.o）

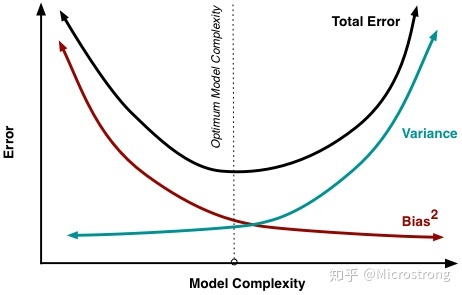
偏差、方差与模型复杂度的关系

方差和偏差加起来最优的点就是模型错误率最小的点，对应的位置就是最佳模型复杂度

偏差也可以称为避免欠拟合，方差被称为避免过拟合，在实际建模过程中，我们可以调整模型函数的参数值，得到多组偏差和方差值，从而判断出最优参数，得到最佳模型，具体方法见下文

1.2 过拟合与欠拟合

我们把模型的实际预测输出与样本的真实输出之间的差异称为 “ 误差 ”

把模型在训练集上的误差称为 “ 训练误差 ” 或 “ 经验误差 ”

把模型在新样本上的误差称为 “ 测试误差 ” 或 “ 泛化误差 ”

我们希望得到泛化误差小的学习器，但由于新样本未知，所以只能尽量使训练误差最小化

训练误差、测试误差与模型复杂度的关系

过拟合是指模型对已知数据（即训练集中的数据）的预测较为准确，但对于未知数据（即测试集数据）的预测结果较差的现象；欠拟合是指对两组数据的预测结果都差的现象

假设我们要训练一个模型来识别树叶，给定下图左边两片叶子作为训练集，然后对右边的新样本进行分类预测，产生的两种结果分别表示为过拟合现象和欠拟合现象

（1）过拟合现象

左边树叶的一个特征是边缘都有锯齿，模型将这一特征记录，并得出一判断标准：树叶边缘都是有锯齿的。于是将右侧上图的叶子判别为不是树叶，因为没有锯齿

一般情况下，在我们构建和训练模型的过程中，造成过拟合的原因如下：

$\bullet$ 样本的特征数量较多而训练样本数目较少，样本选取方法错误，样本标签错误等

$\bullet$ 样本噪声干扰过大

$\bullet$ 模型参数太多，复杂度过高

解决过拟合的方法如下：

$\bullet$ 获取额外数据进行交叉验证

$\bullet$ 重新清洗数据

$\bullet$ 加入正则化项

（2）欠拟合现象

左边树叶的另一个特征是颜色都为绿色，模型学习不到位，将绿色这一粗略特征作为判断树叶的充分必要条件，因此将右侧下图绿色的树也判别为树叶

造成欠拟合的原因如下：

$\bullet$ 样本的特征数量少

$\bullet$ 模型参数太少，复杂度低

解决欠拟合的方法如下：

$\bullet$ 增加新特征，可以加入特征组合、高次特征、多项式特征等

$\bullet$ 减少正则化参数，使用非线性模型，调整模型的容量或使用集成学习方法

1.3 经验风险与结构风险

一般来说，机器学习模型学习过程采用的策略就是使损失函数最小化，同时这也是一个最小化误差的过程，换句话说，最小化误差可通过最小化损失函数达成，这个损失我们称之为 “经验损失”

策略详情请看机器学习概述：https://blog.csdn.net/T940842933/article/details/131606224?spm=1001.2014.3001.5502

规则化模型参数的目标是防止模型过拟合，可通过限制模型的复杂度来达成

奥卡姆剃刀（Occam’s Razor）原理：在模型能够较好地匹配已知数据的前提下，模型越简单越好

模型的 “ 简单 ” 程度可通过模型的参数情况来度量，所以一般采用在经验损失的基础上加上一项关于模型参数复杂度的规则化函数 $J(w)$ 来平衡，加上该约束项的模型我们称之为 “ 结构风险 ”

至此，我们的目标由原来的最小化经验损失变成最小化结构损失，即：

$min\frac{1}{M}\sum_{i=1}^{M}L(y_i,f(x_i;w,b))+\lambda J(w)$

其中，第一项 $\frac{1}{M}\sum_{i=1}^{M}L(y_i,f(x_i))$ 就是经验风险函数，由各种经验损失函数组成；

第二项 $J(w)$ 称为正则化函数，一般是一个关于模型待求权重向量 $w$ 的函数，其值随模型复杂度单调递增

所以，正则化函数项的作用是选择经验风险和模型复杂度同时较小的模型，对应结构风险最小化

1.4 正则化

正则化通过使用范数对权重向量 $w$ 进行约束，在损失函数上加入规则（限制），从而降低模型复杂度，防止模型过拟合

（1）L0范数

权重向量 $w$ 的 $p$ 范数的定义为

$||w||_p=(\sum_{j=1}^{N}|Wj|^p)^{\frac{1}{p}}$

$x_i=(x_{i}^{(1)},x_{i}^{(2)},...,x_{i}^{(N)})$ 表示一个含有N个特征的样本向量

$w=(w_1,w_2,...,w_N)$ 表示的是与样本向量N个特征对应的特征权重向量

$Wj$ 权重系数

L0范数的物理意义可以解为向量中非0元素的个数

我们用L0范数来规则化权重向量 $w$ ，就是希望 $w$ 中的大部分元素都是0，换句话说就是让权重向量 $w$ 是稀疏的

稀疏可以实现特征的自动选择。在训练模型的过程中，我们通常不会用到样本的全部特征，因为有的特征并不重要，全部使用反而会增加模型的复杂度，干扰对样本类别的预测，所以引入稀疏规则化算子，它会学习如何去掉没用的信息特征，即把这些特征对应的权重系数 $Wj$ 置为0

L0范数是一个NP问题，优化求解困难，而L1范数是L0范数的最优凸近似，且容易优化求解，所以往往选择L1范数来正则化而不使用L0范数

（2）L1范数

L1范数是指向量中各个元素绝对值之和，即

$||w||_1=\sum_{j=1}^{N}|w_j|$

L1范数使权重稀疏的过程：

假设原来的经验风险函数为L0，加入正则化项L1，变为结构风险函数L，即

$L= L_0+|w|$

对 $w$ 中的各个元素 $w_j,j=1,2,...,N$ 依次求偏导，得：

$\frac{\partial L}{\partial w_j}=\frac{\partial L0}{\partial w_j}+sign(w_j)$

规定 $sign()$ 是一个符号函数，当 $x>0$ 时 $sign(x)=1$ ；当 $x=0$ 时 $sign(x)=0$ ；当 $x<0$ 时 $sign(x)=-1$

根据梯度下降法， $w$ 得权重更新公式为

$w_j = w_j-\eta (\frac{\partial L_0}{\partial w_j}+sign(w_j))=w_j-\eta \frac{\partial L_0}{\partial w_j}-\eta sign(w_j)$

效果：

当 $w_j$ 为正时，每次更新时相较于不加正则化项， $-\eta sign(w_j)$ 会使 $w_j$ 变小

当 $w_j$ 为负时，每次更新时相较于不加正则化项， $-\eta sign(w_j)$ 会使 $w_j$ 变大

整体效果就是让 $w_j$ 向 0 靠近，使第 $j$ 个特征对应的权重尽可能为 0，这里 $j=1,2,...,N$

注：当 $w_j=0$ 时， $|w_j|$ 不可导，只能按照原始的未经正则化的方法更新 $w_j$ ，即去掉 $sign(w_j)$

（3）L2范数

比L1范式更受欢迎的L2范数，指的是向量各元素的平方和的开方，即

$||w||_2=(\sum_{j=1}^{N}|w_j|^2)^\frac{1}{2}$

与L1正则类似，加L2正则后的结构风险函数变为

$L= L_0+\frac{1}{2}||w||^2$

对 $w$ 中的各个元素 $w_j,j=1,2,...,N$ 依次求偏导，得：

$\frac{\partial L}{\partial w_j}=\frac{\partial L0}{\partial w_j}+w_j$

根据梯度下降法， $w$ 得权重更新公式为

$w_j = w_j-\eta (\frac{\partial L_0}{\partial w_j}+w_j)=(1-\eta )w_j-\eta \frac{\partial L_0}{\partial w_j}$

效果：

与没有加正则化项相比，在添加了L2正则后， $w_j$ 更新变为了 $(1-\eta )w_j$ ，由于 $\eta$ 都是正数，所以 $1-\eta < 1$ ，因此它的效果就是减少 $w_j$ ，这就是所谓的权重衰减