本文详细介绍了数据可视化的图表类型选择依据，包括比较类、分布类、占比类、关联类和趋势类图表的功能性和应用场景。柱状图、气泡图、饼图、雷达图、折线图等常见图表的优缺点被逐一分析，帮助读者根据需求选择合适的图表以清晰有效地展示数据。
目录
图表类型选择的依据
数据可视化图表类型选择，总结下来，需要考虑三点：
- 需要从已有数据出发，考虑想要用数据图表做什么，也就是图表的功能性。比如我要查看公司产品的用户中的各年龄段的占比，如果可分成5个年龄段，那用饼图就比较合适。
- 还要考虑图表对使用者的理解能力要求，也就是可理解性。刚才的例子说到饼图，饼图对于任何人都是比较浅显易懂的，那就不存在问题，如果比较复杂的图形比如桑基图，就要考虑使用人是谁，有没有可能这个图使用人无法理解。
- 然后要考虑图表的可读性，用刚才的例子，5个年龄段，用饼图比较合理，如果是15个年龄段，当然也能用饼图去表现，但是可读性会降低一些，占比1%以下的部分就无法进行比较了。
图表的功能性总结
可视化图表所具有的功能有很多，比如柱状图，通过不同类别的柱长，来代表每一类别数值大小，可起到不同类别之间做比较的功能。有些图表具有多种功能。
比较：显示值与值之间的不同和相似之处。通常使用图形长度、面积、颜色来比较不同分类间数值的大小，也有用宽度、位置、角度等。比如最常见的柱状图，就具有比较的功能。
分布：显示频率，数据分散在一个区间或分组。使用图形的位置、大小、颜色的渐变程度来表现数据的分布，通常用于展示连续数据上数值的分布情况。比如散点图、气泡图等，可以查看、分析数据的分布。
流程：显示流程流转和流程流量。一般流程都会呈现出多个环节，每个环节之间会有相应的流量关系。比如漏斗图，具有流程分析的功能。
占比：可显示同一维度上占比关系。比如饼图，有展示占比的作用。
关联：显示数据之间相互关系。 使用图形的嵌套和位置表示数据之间的关系，通常用于表示数据之间的前后顺序、父子关系以及相关性。比如韦恩图，有展示数据之间关系的作用
趋势：分析数据的变化趋势。使用图形的位置表现出数据在连续区域上的分布，通常展示数据在连续区域上的大小变化的规律。比如折线图，可展示数据随时间变化的趋势
地图：显示地理区域上的数据。使用地图作为背景，通过图形的位置来表现数据的地理位置，通常来展示数据在不同地理区域上的分布情况。比如气泡地图，可展示地图上每个区域的连续数据的大小。
图表类型总结
下面每个功能类型内的具体图表顺序，是按照我理解的最常见到不常见排序的。
比较类
柱状图和柱状图变体
下图是横向柱状图的示例，展示了某年各省份的GDP。
柱状图的基本类型有横向和纵向（也称“条形图”）。演化出的进阶类型有：堆叠柱状图、双向柱状图、分组柱状图、玉玦图（环形柱状图）、南丁格尔玫瑰图。
横向柱状图和纵向柱状图的一大区别在于：横向柱状图可以容纳更多分类。一般来说，横向柱状图适合于少于30个分类，纵向柱状图适合于少于12个分类。下面是横向柱状图的一个例子。
基本的柱状图不多解释了，这里看下其他分类。
堆叠柱状图
下图是堆叠柱状图的一个示例，每种化妆品在各个城市的销售情况。
适合用于二级分类的数据，要展示每个一级分类内部的二级分类的数值。可以形象得展示一个大分类包含的每个小分类的数据，以及各个小分类的占比，显示的是单个项目与整体之间的关系。下面是一个纵向堆叠柱状图的例子。
横向堆叠柱状图和纵向堆叠柱状图的区别也是在于适宜展示的分类数量，上限分别是30和12。
还有一种特殊的堆叠柱状图是展示百分比的堆叠柱状图：柱子的各个层代表的是该类别数据占该分组总体数据的百分比，关注点在百分比而不在具体数量。
下图表是一个游戏公司在不同年份的各类游戏的销量情况。
双向柱状图
下图是双向柱状图的示例。展示了某个公司各个部门对某项任务的完成情况数据的对比，完成人数使用正向柱状图表示、未完成人数使用反向柱状图表示。
双向柱状图（又称“正负条形图”），使用正向和反向的柱子显示类别之间的数值比较。可用来比较两个事物或两个分类的多项数据，比如两个城市、两个公司、及格同学和不及格同学等。双向柱状图基本可以用雷达图替换，可以说在适用范围上，雷达图>双向柱状图。后面再说雷达图。
分组柱状图
下图是分组柱状图的示例，对比了某游戏公司在 2001、2002、2003 这三年的各类游戏的销量情况
分组柱状图大致功能和堆叠柱状图相同，只是堆叠柱状图更方便看到各一级分类的总量，分组柱状图更强调二级分类之间的对比。
玉玦图（环形柱状图）
下图是玉玦图的示例，反应了美国民众对不同领域中的中美问题关注程度。
其实就是柱状图的直接变形，只是审美上占优势，有一个严重缺陷是：具有半径反馈效应。视觉上半径越大的玦环会看起来更大，半径小的则小，所以要使用且不想造成视觉误差就必须要先进行数量排序，但是如果分类本身是带有顺序的，比如我们要统计一个学校本科生各年级的人数，如果用玉玦图且按照数量排序，可能最终图形上线的分类以不符合常理的顺序出现，比如二、四、一、三。所以如果是内部数据分析使用，建议不要用玉玦图，用柱状图就好；如果是用于大屏，可以尝试使用，毕竟大屏的美观性相当重要。
南丁格尔玫瑰图
去年3月某二流报纸展示各国疫情数据时用了南丁格尔玫瑰图，传播效果很好。
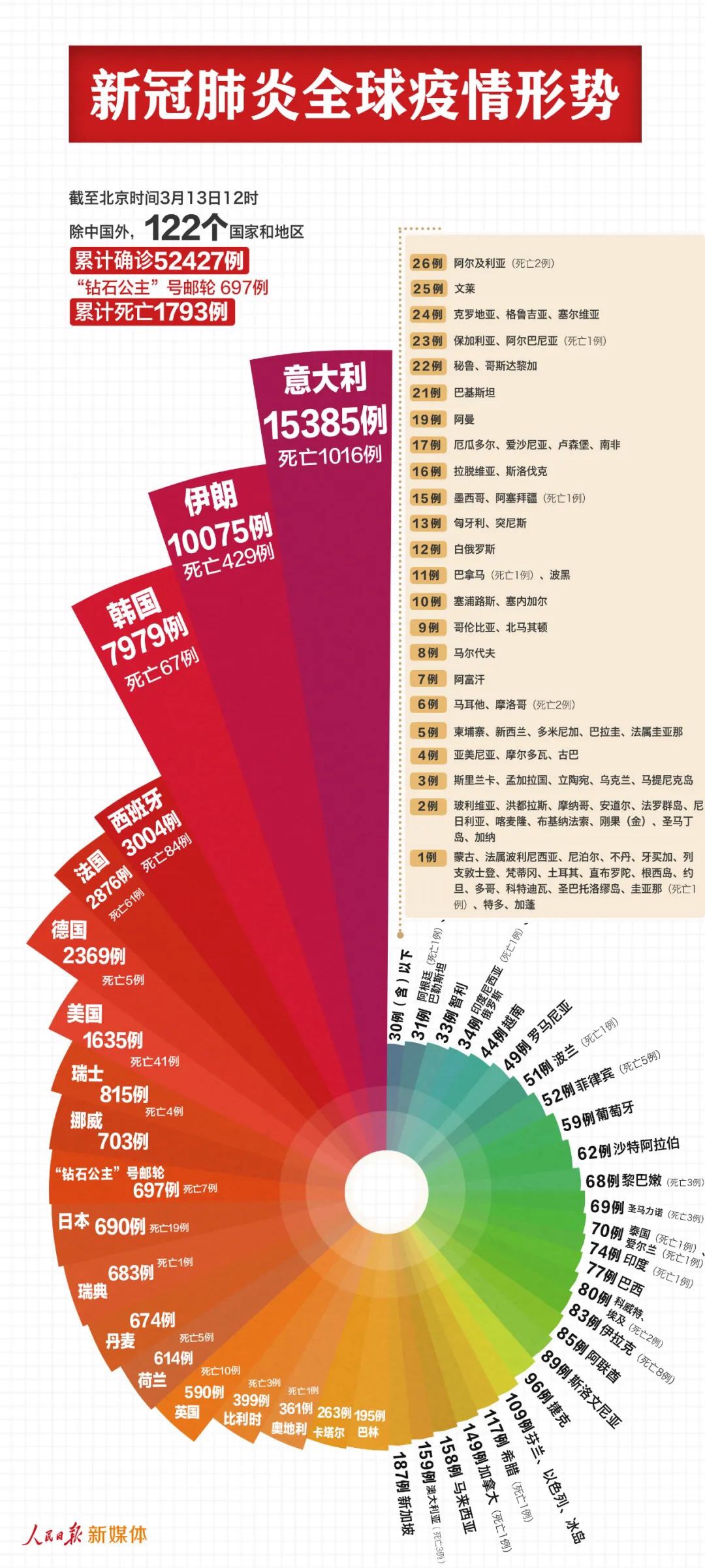
在极坐标下绘制的柱状图，使用圆弧的半径长短表示数据的大小，注意各分类的圆弧角度是相同的。适用于数据量不超过30条的场景，和普通横向柱状图对比，适用场景基本相同，只是南丁格尔玫瑰图会夸大各分类间的差距，且可理解性稍差，建议还是多用柱状图比较好。
气泡图
下图例子，每个气泡代表一个国家，横坐标代表人均GDP，纵坐标代表人均寿命，气泡面积大小代表人口数量。
气泡图具有“比较”功能和“分布”功能。气泡图最基本的用法是使用三个值来确定每个数据序列，一个值作为横坐标，一个值作为纵坐标，一个值作为气泡面积大小。注意这里第三个值不是体现气泡半径大小，而是面积大小。基本的气泡图可体现三个数据维度，当然也可以通过不同颜色增加第四维度。气泡图可以用于对于多维度数据进行探索性分析，可分析数据之间的相关性。
色块图
下图例子是某年股指的波动情况的色块图，每个色块代表一天的股指涨跌幅度，通过365个色块展示了全年365天的涨跌情况，下方有个滑块，可以选择只查看特定数值范围。
色块图具有“比较”功能和“分布”功能。适合用于直接对数据量较大的、相对原始的数据进行分析。
雷达图
下图是日本解说乒乓球比赛时，常用到的六边形雷达图。没有放大名鼎鼎的“帝国破坏龙”的雷达图，因为那个图体现不出雷达图的作用，各维度的数值都到上限了。
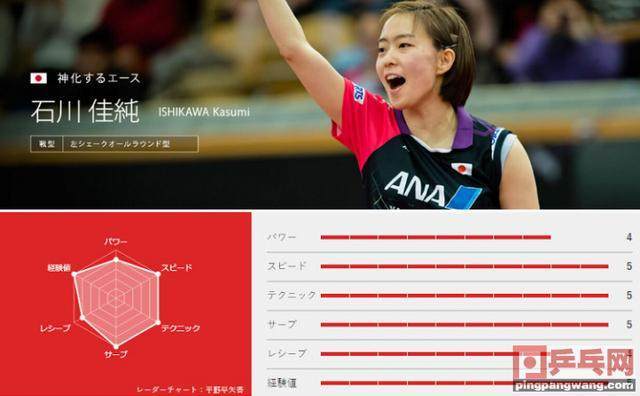
雷达图又叫戴布拉图、蜘蛛网图，可表现多维（4维以上）数据的图表。用于从多个维度评价某个事物（单个多边形），或者用于对比不同事物（多个多边形）。
缺点：多边形过多或数据维度过多，会导致可读性降低。
漏斗图
下图是漏斗图的例子。
漏斗图适用于业务流程比较规范、周期长、环节多的单流程单向分析，通过漏斗各环节业务数据的比较能够直观地发现和说明问题所在的环节，进而做出决策。漏斗图在商业数据可视化中应用很多，就教育行业来说，常见的广告展示、广告点击、客户留下资料、销售转化、最终成交，这个过程在理论上非常适合用漏斗图，但是，实际上不一定。要考虑每一步的转化率是否过小，如果前两步的转化率相乘已经小于1%了，整个图形展示出来，后面几步就跟一根针一样，完全没有可视化的效果，不如直接单纯展示数字不必可做可视化了。当然因为常用可视化库比如echarts，都有点击某环节的图例选择不展示该环节，可以解决这一问题，但是在一开始是不可能有很好的效果的。
下图是对称漏斗图的示例，可以同时对两个业务流程进行分析。
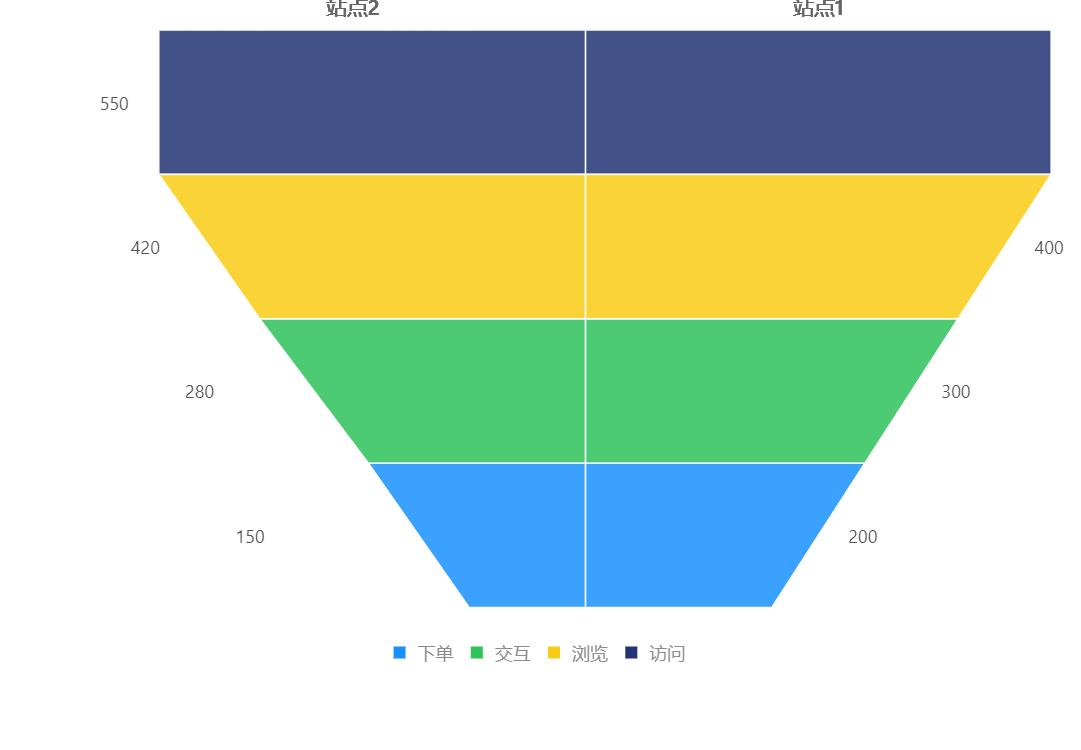
K线图
下图是K线图示例。
K线图解释：
这个常用语展示股票交易数据，对于其他行业来说基本用不上，适用范围比较窄，在此不展开说了。
词云图
下图是词云图的示例。
词云图是专门用于文本数据可视化的图表类型，可用于对比不同文本的某项数值（比如出现频率）的大小。
子弹图
下图是子弹图的示例。
子弹图包含背景色条，表示定性范围，比如优、良、及格、不及格，包含预测值（或目标值）和实际值。适用范围比较窄，且可读性较差，但是在适用场景下会特别好用，比如展示学生成绩。
分布类
箱形图（盒须图、盒式图、箱线图）
箱形图（Box Chart）我查了资料后发现有两种，我暂时将这两种称为简版箱形图和进阶箱形图，哪位朋友如果有更好的叫法可以告诉我。
下面是基本箱形图的一个例子，展示了鸢尾花数据的花萼长度、花萼宽度、花瓣长度、花瓣宽度四个数据维度的分布情况。
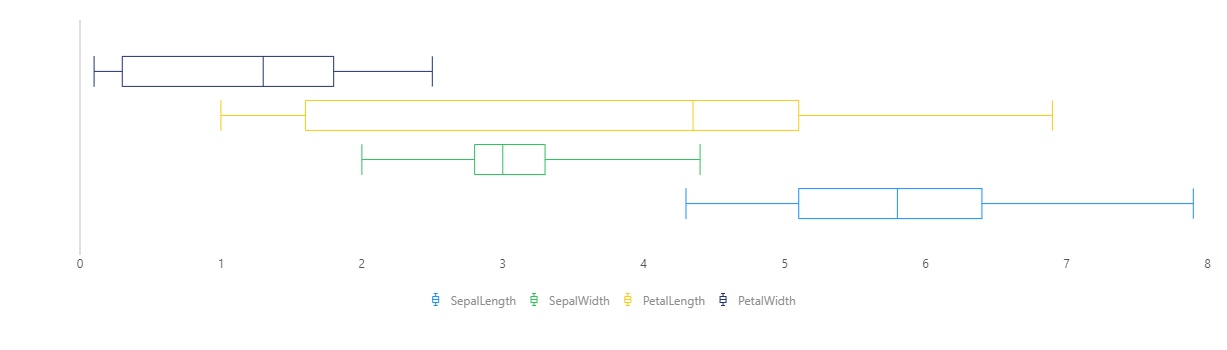
下图解释了箱形图的含义。
每个维度的数据取上图中的五个点可绘制出箱形图，这是简版箱形图。这种箱形图是比较容易理解的，适用于比较多组数据的分布情况，
可以观察到：
- 一组数据的关键值：中位数、最大值、最小值等。
- 数据是否是对称的。
- 这组数据的分布是否密集、集中。
下面是进阶箱型图的例子
下图是进阶箱形图的解释图
一组数据，下四分位数记为Q1，中位数记为Q2，上四分位数记为Q3，这里不多解释分位数的概念了。四分位间距IQR=Q3-Q1，下限 = Q1-1.5*IQR，注意这里说的是下限，不是下边缘，下边缘是这组数据中大于下限（Q1-1.5*IQR）所有的数值中的最小值，上限 = Q3+1.5*IQR，上边缘是这组数据中小于上限的所有数值的最大值，超出上边缘和下边缘的数值作为异常值，以圆圈等形状做特殊标记。
如果特别关注异常值，可以把异常值分成两类，下面是解释图。
这里的上下限有两种，一种是温和异常值上下限，距离Q1和Q3是1.5倍IQR（四分位间距）；另外一种是极端异常值上下限，距离Q1和Q3是3倍的IQR。超过温和异常值上下限且不超过极端异常值上下限的数值，是温和异常值；超过极端异常值上下限的数值，是极端异常值。温和异常值和极端异常值用不同形状符号标记
写了这么多，才能把这种进阶箱形图解释清楚，足以证明箱形图的可理解性稍差，但随之带来的就是，如果有一个有相关知识背景的图表使用人，可以通过一个箱形图获得相当丰富的信息量，信息密度或者说信噪比极高。
从进阶箱形图中我们可以观察到：
- 一组数据的关键值：中位数、四分位数、最大值、最小值、异常值、去掉异常值的最大值和最小值等。
- 数据是否是对称的。
- 这组数据的分布是否密集、集中。
气泡图
见比较类-气泡图
色块图
见比较类-色块图
分布曲线图
未完待续
热力图
下图是杭州房租热力图，用于显示杭州市房租价格分布。每个位置的颜色越深，代表该位置的房价越高。
热力图一般出现在地图上，也可以用在直角坐标系上，一般边界经平滑处理，每个位置的颜色深度代表该位置的连续数据大小，比如上图就是房价。
热力图的可理解性、可读性非常强，只是需要一个合适的使用场景，比如地区的房价、地区的人口，总之跟地图结合展示某个连续数据非常合适。
直方图
直方图有两种，下图是原始的标准的直方图的示例，展示了一组员工身高数据的分布，X轴表示这组员工的高度，每个矩形的面积表示数量。比如170cm<=员工高度<172cm的数量为20，则该矩形面积为20，X轴宽度为2，Y轴高度为10。
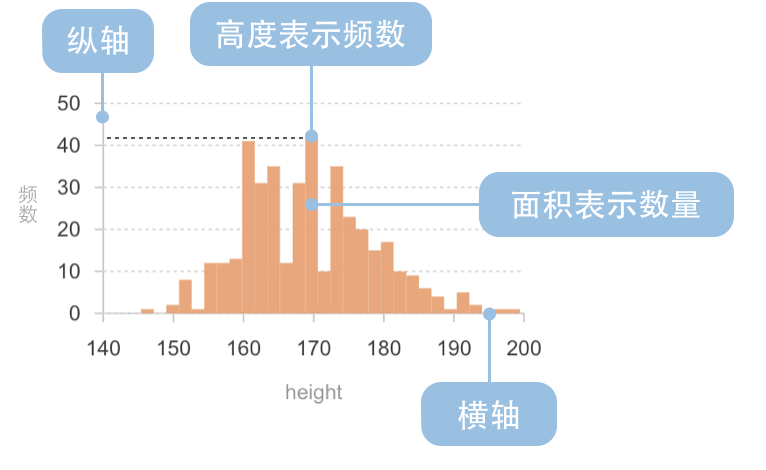
直方图的特点是，相邻矩形是无间隔的，因为X轴是连续变量，这和柱状图不同，虽然看上去有些像。因为用面积表示数量大小，所以每个矩形的X轴宽度不一定是相同的，当然一般来说我们会尽量保证各矩形的X轴宽度相同。
下图是非标准的直方图，高度表示数量。
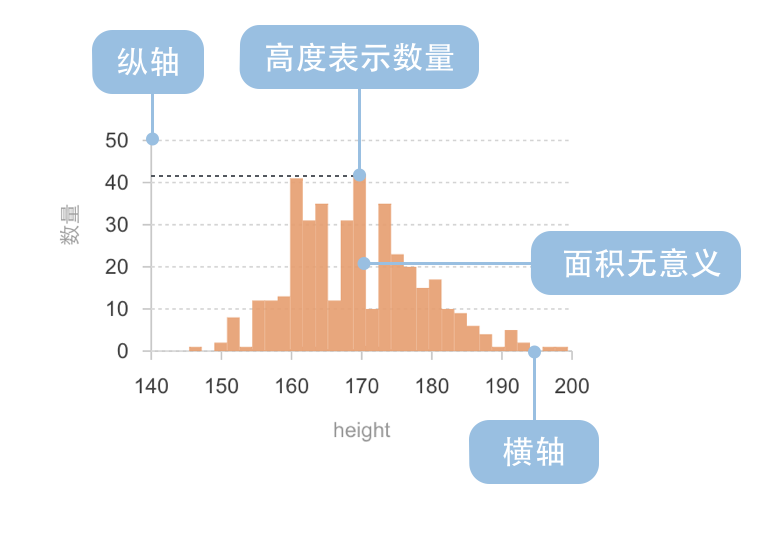
非标准的直方图更容易被其他人理解，因为用高度代表每个矩形的数量，这就要求每个矩形的X轴宽度必须相同，如上图都是2cm，否则很可能出现歧义。
占比类
饼图
下面是饼图的一个示例，展示了一个游戏公司的各类游戏的销售额占比。
饼图用于展示每个分类占总体的比例，在占比类图表中最为常见。饼图相比其他图表而言信息密度很低，但是人民群众喜闻乐见，因为易于理解，所以适合汇报工作使用。饼图不适合分类过多的场景，一般分类超过9个，就不再适用于饼图，可以使用横向柱状图，分类在30个以内就适用。饼图不适合各分类占比相差不多的场景，如果遇到几个分类的占比差距不大，那建议使用柱状图。
环图（环形图、甜甜圈图）
下面是环图的一个示例，展示了一个游戏公司的各类游戏的销售额占比，和上面的饼图是相同的数据。
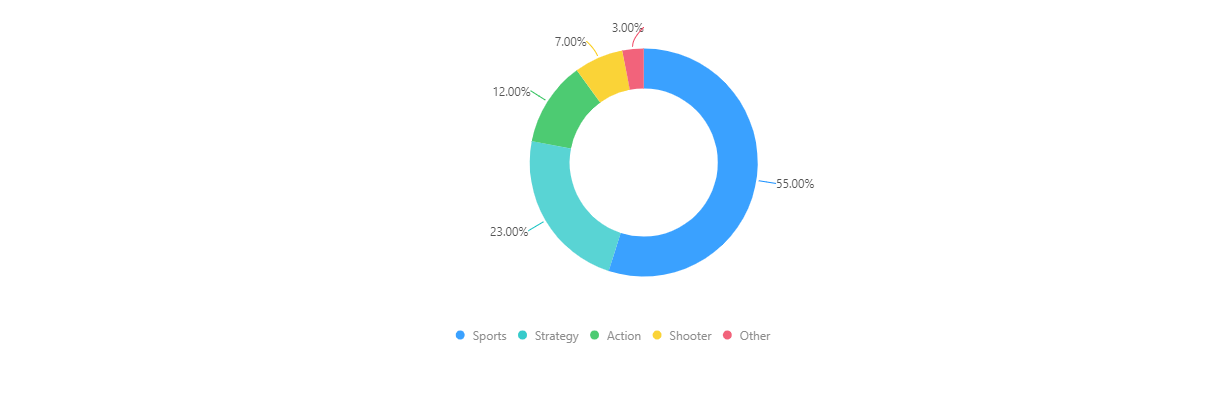
环图相对于饼图空间的利用率更高，我们可以使用它的空心区域显示文本信息，比如标题等。它与饼图的优缺点类似。
堆叠柱状图
见比较类-柱状图
堆叠面积图
下图是堆叠面积图的一个示例，展示了游戏公司在2001，2002，2003，2004 几年内不同分类的游戏的销售情况。
堆叠面积图具有体现部分占总体比例和体现趋势的作用，可查看总量的变化趋势，也可以查看分量的变化趋势。堆叠面积图适合场景：要展示不同分类的数据随时间变化的趋势，同时映射到颜色的分类不超过12个。上图Y轴表示数量，还有一种堆叠面积图，Y轴表示百分比，可称为百分比堆叠柱状图。
下面是一个百分比堆叠柱状图的示例，展示了某APP在几个月内不同版本的占比。
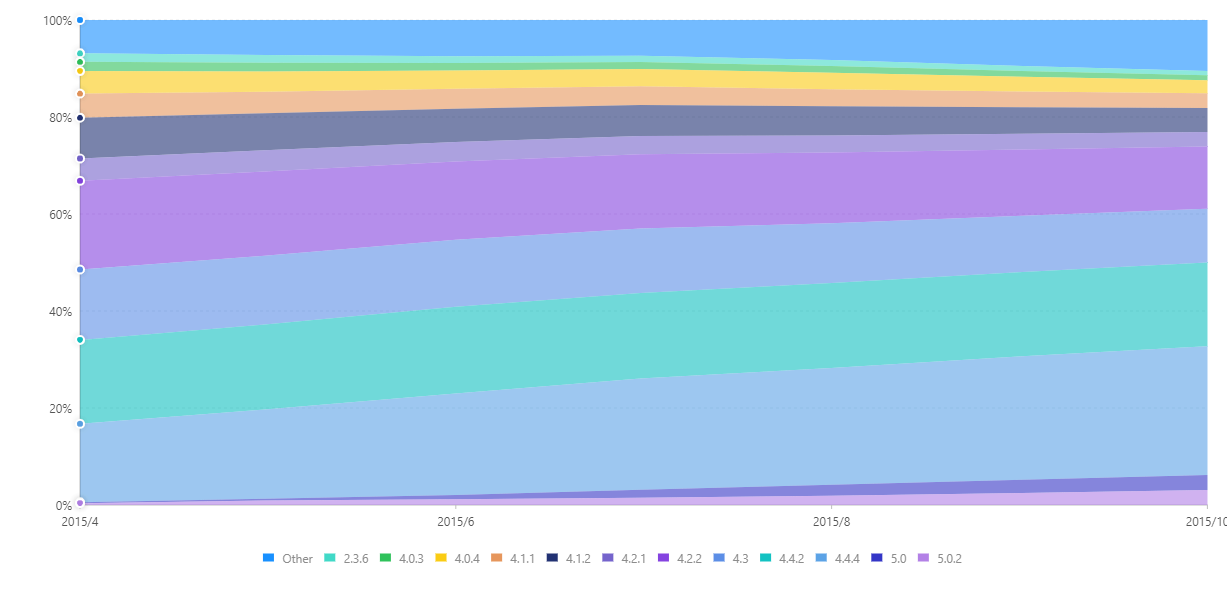
关联类
桑基图
下图是桑基图的一个示例。展示了2014年中国各类能源的去处。
桑基图用于描述一组值到另一组值的流向，需要起始流量和结束流量相同，节点不同的宽度代表了特定状态下的流量大小。桑基图通常应用于能源、材料成分、金融等数据的可视化分析。
趋势类
折线图
下图是折线图的一个示例。显示了两个App在App Store的近七日的每日下载量。
折线图是基本的展示数据随时间趋势的图表，折线图中有多条折线时，也具有对比不同类别的数据的作用。在折线图中，数据是递增还是递减、增减的速率、增减的规律（周期性、螺旋性等）、峰值等特征都可以清晰地反映出来。一个折线图中，折线不能过多，最多不能超过5条。
面积图
面积图包含一般面积图和堆叠面积图，一般面积图的示例如下图，展示了某只股票在 2015 年 9 月份整个月的每日的价格走势。
堆叠面积图
见占比类-堆叠面积图
K线图
见比较类-K线图
回归曲线图
下图是回归曲线图的一个示例，农业科研机构要研究最大积雪深度 x 与灌溉面积 y 之间的关系，提供的数据样本为近 10 年的数据，描点在直角坐标系后，基本可以看出符合y和x之间有线性相关性，可根据最小二乘法画出一条线性回归线。
回归曲线图同统计学紧密结合，属于探索型图表，通过对样本数据进行曲线回归（非线性回归）确定两个变数间数量变化的某种特定的规则或规律。我们称图中的线为回归曲线，是最准确地贯穿图中的各个点的线，分为线性回归和非线性回归。回归曲线图需要观察各点的位置，或者通过统计学知识来确定两个变量的关系，这是绘制回归曲线图的难点。
地图类
气泡地图
下图是气泡地图的一个示例，展示了2013年统计的各国人口数量。
气泡地图，是气泡图和地图的结合，以地图为背景，在上面绘制圆形气泡，气泡面积大小代表要表达的数据的大小。气泡地图适用于比较带地理信息的数据的大小。气泡地图主要缺点是当地图上的气泡过多过大时，气泡间会相互遮盖而影响数据展示。
分级统计地图
下图是分级统计地图的一个示例，展示了2008年美国各州的肥胖率。
分级统计地图通常用不同颜色来表示每个地区的数据大小，比如上图是用7种颜色表示不同洲的肥胖率。
下图是一种非严格意义上的分级统计地图，展示了2020年美国大选的各州票数和最终选举人，看地图的颜色好像两者势均力敌甚至川普更有优势，实际票数是川普落后很多，这就是因为川普的票区相比于票数来说面积更大，比如北方的MT蒙大拿州只有3票，但是面积很大，造成了视觉上的误差。
点描法地图
下图是点描法地图的一个示例，展示了2010 年芝加哥人口种族分布，用不同颜色的点在地图上标识不同的种族，粉红色表示白人，蓝色表示黑人，绿色表示亚洲人，黄色表示拉丁美洲人。
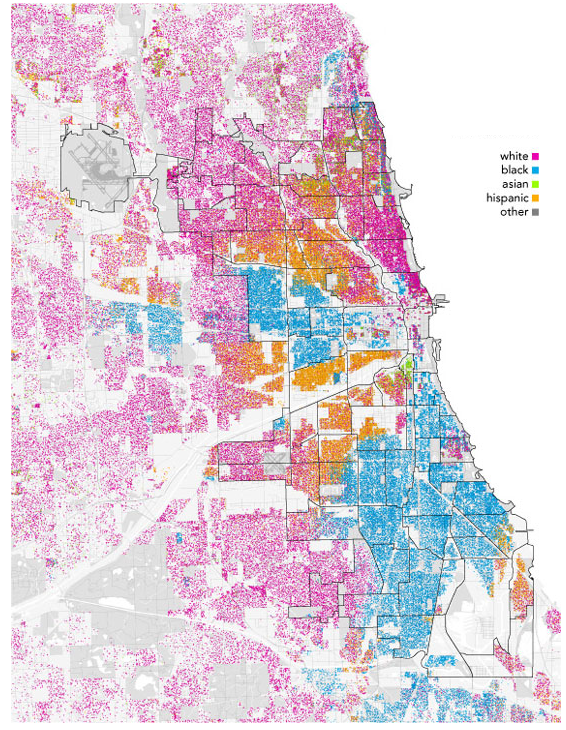
点描法地图，一个点代表一个数据或者一个对象，比如上图，一个点代表在该位置的一个人。
本文主要借鉴了AntV的图表用法介绍，在此基础上，加入了自己的理解，剔除了我认为价值不大的图表类型和内容。
扫一扫
487
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
