1树的基础部分
1.1二叉树
1.1.1为什么使用树这种数据结构
- 数组存储方式的分析优点:通过下标方式访问元素,速度快。对于有序数组,还可使用二分查找提高检索速度。缺点:如果要检索具体某个值,或者插入值(按一定顺序)会整体移动,效率较低。
- 示意图:
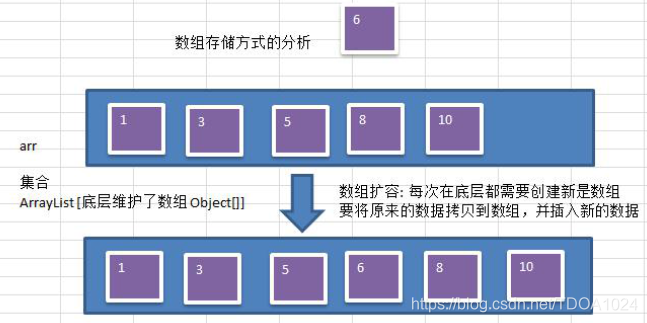
- 链式存储方式的分析优点:在一定程度上对数组存储方式有优化(比如:插入一个数值节点,只需要将插入节点,链接到链表中即可, 删除效率也很好)。缺点:在进行检索时,效率仍然较低,比如(检索某个值,需要从头节点开始遍历)
- 示意图:
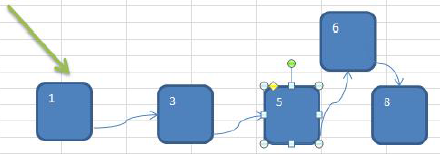
- 树存储方式的分析能提高数据存储,读取的效率, 比如利用 二叉排序树(Binary Sort Tree),既可以保证数据的检索速度,同时也可以保证数据的插入,删除,修改的速度。案例: [7, 3, 10, 1, 5, 9, 12]
- 示意图:
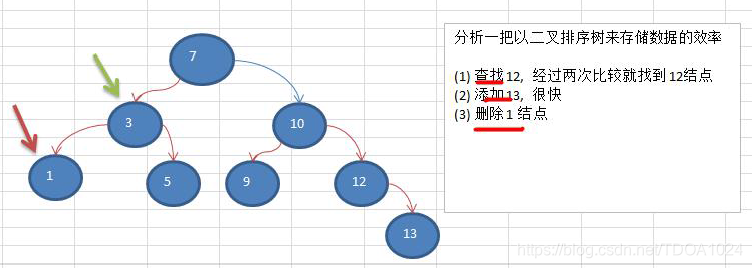
1.1.2树的示意图
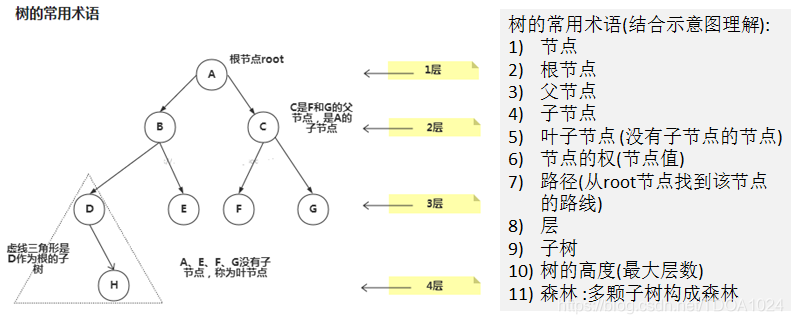
1.1.3二叉树的概念
- 树有很多种,每个节点最多只能有两个子节点的一种形式称为二叉树。
- 二叉树的子节点分为左节点和右节点。

- 如果该二叉树的所有叶子节点都在最后一层,并且结点总数= 2^n -1 , n 为层数,则我们称为满二叉树。
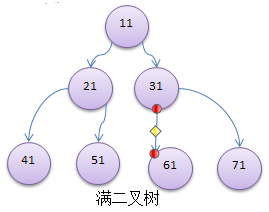
- 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层,而且最后一层的叶子节点在左边连续,倒数第二层的叶子节点在右边连续,我们称为完全二叉树。
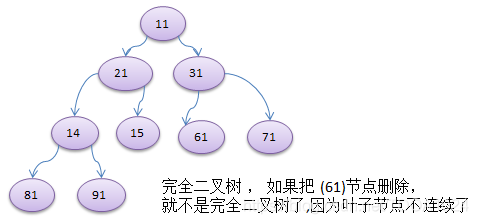
1.1.4二叉树遍历的说明
使用前序,中序,后序对二叉树进行遍历
- 前序遍历:先输出父节点,再遍历左子树和右子树
- 中序遍历:先遍历左子树,再输出父节点,再遍历右子树
- 后续遍历:先遍历左子树,再遍历右子树,最后输出父节点
- 总结:看输出父节点的顺序,就是前序,中序还是后序
1.1.5二叉树遍历应用实例(前序、中序、后序)
- 应用实例的说明和思路

- 代码实现
/**
* @author Wnlife
* @create 2019-11-25 21:01
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
/*创建二叉树*/
BinaryTree binaryTree=new BinaryTree();
/*创建需要的结点*/
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
/*构建二叉树之间的关系*/
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
/*测试前序遍历: 1,2,3,5,4*/
System.out.println("前序遍历~~");
binaryTree.preOrder();
/*测试中续遍历: 2,1,5,3,4*/
System.out.println("中序遍历~~");
binaryTree.infixOrder();
/*测试后序遍历: 2,5,4,3,1*/
System.out.println("后序遍历~~");
binaryTree.postOrder();
}
}
/**
* 创建二叉树
*/
class BinaryTree{
/*根节点*/
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
/**
* 前序遍历
*/
public void preOrder(){
if(this.root!=null){
this.root.preOrder();
} else{
System.out.println("二叉树为空,无法遍历");
}
}
/**
* 中序遍历
*/
public void infixOrder(){
if(this.root!=null){
this.root.infixOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
/**
* 后序遍历
*/
public void postOrder(){
if(this.root!=null){
this.root.postOrder();
}else{
System.out.println("二叉树为空,无法遍历");
}
}
}
/**
* 创建HeroNode节点
*/
class HeroNode{
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public String getName() {
return name;
}
public HeroNode getLeft() {
return left;
}
public HeroNode getRight() {
return right;
}
public void setNo(int no) {
this.no = no;
}
public void setName(String name) {
this.name = name;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
/**
* 前序遍历
*/
public void preOrder(){
/*先输出当前节点*/
System.out.println(this);
/*左子节点不为空,递归遍历左子树*/
if(this.left!=null){
this.left.preOrder();
}
/*右子节点不为空,递归遍历右子树*/
if(this.right!=null){
this.right.preOrder();
}
}
/**
* 中序遍历
*/
public void infixOrder(){
/*左子节点不为空,递归遍历左子树*/
if(this.left!=null){
this.left.infixOrder();
}
/*输出当前节点*/
System.out.println(this);
/*右子节点不为空,递归遍历右子树*/
if(this.right!=null){
this.right.infixOrder();
}
}
/**
* 后续遍历
*/
public void postOrder(){
/*左子节点不为空,递归遍历左子树*/
if(this.left!=null){
this.left.postOrder();
}
/*右子节点不为空,递归遍历右子树*/
if(this.right!=null){
this.right.postOrder();
}
/*最后遍历当前节点*/
System.out.println(this);
}
}
1.1.6二叉树-查找指定节点
- 请编写前序查找,中序查找和后序查找的方法
- 并分别使用三种查找方式,查找 heroNO = 5 的节点
- 并分析各种查找方式,分别比较了多少次
思路分析图解:
 代码实现:
代码实现:
/**
* @author Wnlife
* @create 2019-11-25 21:01
* 二叉树
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
/*创建二叉树*/
BinaryTree binaryTree = new BinaryTree();
/*创建需要的结点*/
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
/*构建二叉树之间的关系*/
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
/**
* 测试前序遍历查找
* 前序遍历的次数 :4
*/
System.out.println("前序遍历查找~~");
HeroNode heroNode1 = binaryTree.preOrderSearch(5);
System.out.println(heroNode1);
/**
* 测试中序遍历查找
* 中序遍历的次数 :3
*/
System.out.println("中序遍历查找~~");
HeroNode heroNode2 = binaryTree.infixOrderSearch(5);
System.out.println(heroNode2);
/**
* 测试后序遍历查找
* 后序遍历的次数 :2
*/
System.out.println("后序遍历查找~~");
HeroNode heroNode3 = binaryTree.postOrderSearch(5);
System.out.println(heroNode3);
}
}
/**
* 创建二叉树
*/
class BinaryTree {
/*根节点*/
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
/**
* 前序遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode preOrderSearch(int no) {
if (root != null) {
return root.preOrderSearch(no);
}
return null;
}
/**
* 中序遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
}
return null;
}
/**
* 后续遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode postOrderSearch(int no) {
if (root != null) {
return root.postOrderSearch(no);
}
return null;
}
}
/**
* 创建HeroNode节点
*/
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public String getName() {
return name;
}
public HeroNode getLeft() {
return left;
}
public HeroNode getRight() {
return right;
}
public void setNo(int no) {
this.no = no;
}
public void setName(String name) {
this.name = name;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
/**
* 前序遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode preOrderSearch(int no) {
System.out.println("进入前序查找");
/*首选判断当前节点的值和要查找的值是否相等*/
if (this.no == no) {
return this;
}
/**
* 若当前节点的值不等于要查找的值,则判断左子节点是否为空,
* 若不为空,则递归的遍历左子树,若找到则返回
*/
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
if (resNode != null) {
return resNode;
}
}
/**
* 若左子树没有找到,则判断右子节点是否为空,
* 若不为空,则递归遍历右子树查找
*/
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
/**
* 中序遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode infixOrderSearch(int no) {
HeroNode resNode = null;
/*首先判断左子节点是否为空,若不为空,递归的遍历左子树,若找到则返回*/
if (this.left != null) {
resNode = this.left.infixOrderSearch(no);
if (resNode != null) {
return resNode;
}
}
System.out.println("进入中序查找");
/*若左子树没有找到,则判断当前节点是否满足,若满足则返回*/
if (this.no == no) {
return this;
}
/*若当前节点不满足,则递归的遍历右子树*/
if (this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
/**
* 后续遍历查找
*
* @param no 要查找的编号
* @return 查找到的结果,没有找到返回null
*/
public HeroNode postOrderSearch(int no) {
HeroNode resNode = null;
/*首先判断左子节点是否为空,若不为空,递归的遍历左子树,若找到则返回*/
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
if (resNode != null) {
return resNode;
}
}
/*若左子树没有找到,则判断右子节点是否为空,不为空时递归遍历右子树*/
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
if (resNode != null) {
return resNode;
}
}
System.out.println("进入后序查找");
/*若右子树也没找到,则判断当前节点是否满足*/
if (this.no == no) {
return this;
} else {
return null;
}
}
}
1.1.7二叉树删除指定节点
要求:
- 如果删除的节点是叶子节点,则删除该节点
- 如果删除的节点是非叶子节点,则删除该子树
- 测试,删除掉 5号叶子节点 和 3号子树.
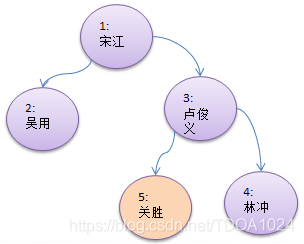
代码:
/**
* @author Wnlife
* @create 2019-11-25 21:01
* 二叉树
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
/*创建二叉树*/
BinaryTree binaryTree = new BinaryTree();
/*创建需要的结点*/
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吴用");
HeroNode node3 = new HeroNode(3, "卢俊义");
HeroNode node4 = new HeroNode(4, "林冲");
HeroNode node5 = new HeroNode(5, "关胜");
/*构建二叉树之间的关系*/
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
/*删除节点测试*/
System.out.println("删除之前的前序遍历:");
binaryTree.preOrder(); //1,2,3,5,4
binaryTree.delNdoe(5);
System.out.println("删除之后的前序遍历:");
binaryTree.preOrder(); //1,2,3,4
}
}
/**
* 创建二叉树
*/
class BinaryTree {
/*根节点*/
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
/**
* 前序遍历
*/
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空,无法遍历");
}
}
/**
* 删除指定节点:
* 1.如果删除的节点是叶子节点,则删除该节点
* 2.如果删除的节点是非叶子节点,则删除该子树
*
* @param no 要删除节点的编号
*/
public void delNdoe(int no){
if(root!=null){ //判断根节点是否为空
if(root.getNo()==no){ //如果根节点为要删除的节点,则删除根节点
root=null;
}else {
root.delNode(no); //如果根节点不是要删除的节点,则递归的删除子树
}
}else { //如果根节点为空
System.out.println("要删除的树是空树,无法删除~~");
}
}
}
/**
* 创建HeroNode节点
*/
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public String getName() {
return name;
}
public HeroNode getLeft() {
return left;
}
public HeroNode getRight() {
return right;
}
public void setNo(int no) {
this.no = no;
}
public void setName(String name) {
this.name = name;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
/**
* 删除节点:
* 1.如果删除的节点是叶子节点,则删除该节点
* 2.如果删除的节点是非叶子节点,则删除该子树
*
* 思路:
* 1.如果左子节点不为空,则判断左子节点是不是要删除的节点,
* 如果左子节点是要删除的节点,则删除左子节点,
* 如果左子节点不是要删除的节点,则递归的删除左子树
* 2.如果左子节点没有找到要删除的节点,则去右子节点找,
* 如果右子节点是要删除的节点,则删除右子节点,
* 如果右子节点不是要删除的节点,则递归的删除右子树
*
* @param no 要删除节点的编号
*/
public void delNode(int no){
if(this.left!=null){
if(this.left.no==no){
this.left=null;
return;
}
this.left.delNode(no);
}
if(this.right!=null){
if(this.right.no==no){
this.right=null;
return;
}
this.right.delNode(no);
}
}
/**
* 前序遍历
*/
public void preOrder() {
/*先输出当前节点*/
System.out.println(this);
/*左子节点不为空,递归遍历左子树*/
if (this.left != null) {
this.left.preOrder();
}
/*右子节点不为空,递归遍历右子树*/
if (this.right != null) {
this.right.preOrder();
}
}
}
1.1.8顺序存储二叉树
- 概念
从数据存储来看,数组存储方式和树的存储方式可以相互转换,即数组可以转换成树,树也可以转换成数组,看下面的示意图。
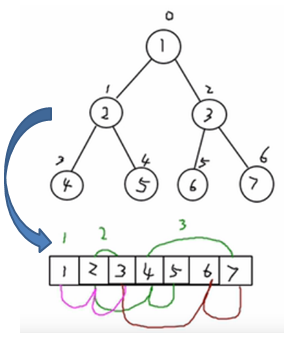
- 要求:
- 右图的二叉树的结点,要求以数组的方式来存放 arr : [1, 2, 3, 4, 5, 6, 6]
- 要求在遍历数组 arr时,仍然可以以前序遍历,中序遍历和后序遍历的方式完成结点的遍历
- 特点:
- 顺序二叉树通常只考虑完全二叉树
- 第n个元素的左子节点为 2 * n + 1
- 第n个元素的右子节点为 2 * n + 2
- 第n个元素的父节点为 (n-1) / 2
- n : 表示二叉树中的第几个元素(按0开始编号如图所示)
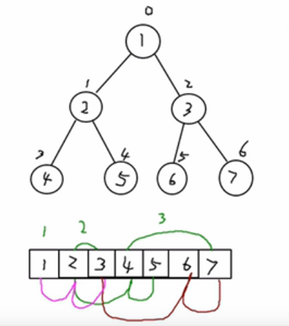
- 实例演示:
需求: 给你一个数组 {1,2,3,4,5,6,7},要求以二叉树前序、中序、后序的方式进行遍历。
代码:
/**
* @author Wnlife
* @create 2019-11-28 19:03
* <p>
* 编写一个ArrayBinaryTree, 实现顺序存储二叉树遍历
*/
public class ArrBinaryDemo {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
ArrBinaryTree abt = new ArrBinaryTree(arr);
System.out.println("前序遍历~~");
abt.preOrder();//1 2 4 5 3 6 7
System.out.println("中续遍历~~");
abt.infixOrder();//4 2 5 1 6 3 7
System.out.println("后续遍历~~");
abt.postOrder();//4 5 2 6 7 3 1
}
}
/**
* 顺序存储二叉树
*/
class ArrBinaryTree {
private int[] arr;
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
public void preOrder() {
preOrder(0);
}
/**
* 二叉树顺序存储的前序遍历
*
* @param index 数组的角标
*/
private void preOrder(int index) {
if (arr == null || arr.length == 0) {
System.out.println("数组为空~~");
return;
}
//输出当前值
System.out.println(arr[index] + " ");
//递归的输出左子树的值
if (2 * index + 1 < arr.length) {
preOrder(2 * index + 1);
}
//递归的输出右子树的值
if (2 * index + 2 < arr.length) {
preOrder(2 * index + 2);
}
}
public void infixOrder() {
infixOrder(0);
}
/**
* 二叉树顺序存储的中序遍历
*
* @param index 数组的角标
*/
public void infixOrder(int index) {
if (arr == null || arr.length == 0) {
System.out.println("数组为空~~");
return;
}
//递归输出左子节点
if (index * 2 + 1 < arr.length) {
infixOrder(index * 2 + 1);
}
//输出自己本身的值
System.out.println(arr[index]+" ");
//递归输出右子节点
if (index * 2 + 2 < arr.length) {
infixOrder(index * 2 + 2);
}
}
public void postOrder() {
postOrder(0);
}
/**
* 二叉树顺序存储的后续遍历
*
* @param index
*/
public void postOrder(int index) {
if (arr == null || arr.length == 0) {
System.out.println("数组为空~~");
return;
}
//先输出左子节点
if (index * 2 + 1 < arr.length) {
postOrder(index * 2 + 1);
}
//再输出右子节点
if (index * 2 + 2 < arr.length) {
postOrder(index * 2 + 2);
}
//输出自己本身的值
System.out.println(arr[index]+" ");
}
}
1.1.9线索化二叉树
1. 先看一个问题
将数列 {1, 3, 6, 8, 10, 14 } 构建成一颗二叉树. n+1=7
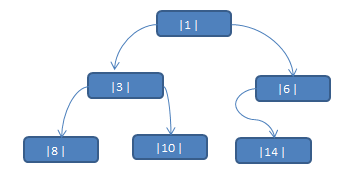
- 问题分析:
- 当我们对上面的二叉树进行中序遍历时,数列为 {8, 3, 10, 1, 14, 6 }
- 但是 6, 8, 10, 14 这几个节点的 左右指针,并没有完全的利用上.
- 如果我们希望充分的利用 各个节点的左右指针, 让各个节点可以指向自己的前后节点,怎么办?
- 解决方案-线索二叉树
2. 线索二叉树基本介绍
- n个结点的二叉链表中含有n+1 【公式 2n-(n-1)=n+1】 个空指针域。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")
- 这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种
- 一个结点的前一个结点,称为前驱结点
- 一个结点的后一个结点,称为后继结点
3. 线索二叉树应用案例【中序线索二叉树】
应用案例说明:将下面的二叉树,进行中序线索二叉树。中序遍历的数列为 {8, 3, 10, 1, 14, 6}
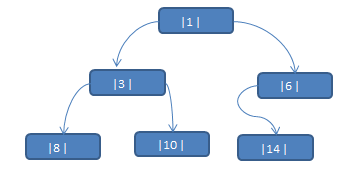
思路分析: 中序遍历的结果:{8, 3, 10, 1, 14, 6}
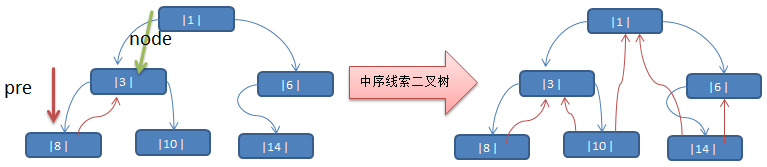
说明: 当线索化二叉树后,Node节点的 属性 left 和 right ,有如下情况:
- left 指向的是左子树,也可能是指向的前驱节点. 比如 ① 节点 left 指向的左子树, 而 ⑩ 节点的 left 指向的就是前驱节点.
- right指向的是右子树,也可能是指向后继节点,比如 ① 节点right 指向的是右子树,而⑩ 节点的right 指向的是后继节点.
/**
* 按照【中序遍历】的顺序对二叉树进行线索化的方法
*
* @param node 当前需要线索化的节点
*/
public void infexThreadedNodes(HeroNode node) {
//一、当前节点为空,则不要进行线索化
if (node == null) {
return;
}
//二、先线索化左子节点
infexThreadedNodes(node.getLeft());
//线索化当前节点
//1.先处理当前节点的前驱节点
if (node.getLeft() == null) {
//让当前节点的左指针指向前驱节点
node.setLeft(pre);
//修改当前节点的左指针类型,指向前驱节点
node.setLeftType(1);
}
//2.处理后继节点
if (pre != null && pre.getRight() == null) {
//让前驱节点的右指针指向当前节点
pre.setRight(node);
//修改当前前驱节点的右指针类型
pre.setRightType(1);
}
pre = node;//当前节点都是下一个前驱节点
//三、线索化右子节点
infexThreadedNodes(node.getRight());
}
遍历线索化二叉树
说明:对前面的中序线索化的二叉树, 进行遍历
分析:因为线索化后,各个结点指向有变化,因此原来的遍历方式不能使用,这时需要使用新的方式遍历线索化二叉树,各个节点可以通过线型方式遍历,因此无需使用递归方式,这样也提高了遍历的效率。 遍历的次序应当和中序遍历保持一致。
/**
* 按照【中序遍历】的方式进行线索化遍历二叉树
*/
public void infixThreadedList() {
HeroNode curNode = root;//定义一个变量,存储当前遍历的结点,从root开始
while (curNode != null) {
/**
* 找到中序遍历线索化二叉树时的第一个节点,
* 循环的找到leftType==1的节点,第一个找到的就是8节点,
* 后面随着遍历而变化,因为当leftType==1,说明该节点是按照线索化处理后的有效节点
*/
while (curNode.getLeftType() == 0) {
curNode = curNode.getLeft();
}
//打印出当前这个节点
System.out.println(curNode);
//如果当前节点的都是指向的都是后继节点,就一直输出
while (curNode.getRightType() == 1) {
//获取当前节点的后继节点
curNode = curNode.getRight();
System.out.println(curNode);
}
//替换这个遍历的节点
curNode = curNode.getRight();
}
}
前序线索化
线索化后的二叉树示意图:
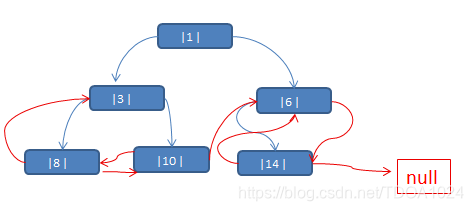
代码:
/**
* 按照【前序遍历】的方式线索化二叉树
*
* @param node 当前需要线索化的节点
*/
public void preThreadedNodes(HeroNode node) {
//一、如果当前节点为空,则直接返回
if (node == null) {
return;
}
//二、先线索化当前节点
//1.设置当前节点的前驱节点
if (node.getLeft() == null) {
//设置当前节点的前驱节点
node.setLeft(pre);
//设置当前节点的类型
node.setLeftType(1);
}
//2.设置后继节点
if (pre != null && pre.getRight() == null) {//1 3 8 10 6 14
//设置上一个节点的后继节点
pre.setRight(node);
//设置后继节点的类型
pre.setRightType(1);
}
//当前节点成为下一个节点的前驱节点
pre = node;
//三、线索化当前节点的左子树
if (node.getLeftType() != 1) {
preThreadedNodes(node.getLeft());
}
//四、线索化当前节点的右子树
if (node.getRightType() != 1) {
preThreadedNodes(node.getRight());
}
}
/**
* 按照【前序遍历】的方式遍历线索化二叉树
*/
public void preThreadedList() {
HeroNode curNode = root;//定义一个变量,存储当前遍历的结点,从root开始
while (curNode != null) {
//遇到先对其进行进行访问,再对其左子树进行遍历访问,直到找到最左的那个节点;
while (curNode.getLeftType() == 0) {
System.out.println(curNode);
curNode = curNode.getLeft();
}
//再根据线索化的指向对其右子树进行遍历访问。
System.out.println(curNode);
curNode = curNode.getRight();
}
}
后序线索化
线索化后的示意图

代码:【后序线索化时增加了指向父节点的指针】
/**
* 按照【后序遍历】的方式线索化二叉树
*
* @param node 当前需要线索化的节点
*/
public void postThreadedNodes(HeroNode node) {
//一、如果当前节点为空,则直接返回
if (node == null) {
return;
}
//二、线索化当前节点的左子树
postThreadedNodes(node.getLeft());
//三、线索化当前节点的右子树
postThreadedNodes(node.getRight());
//四、先线索化当前节点
//1.设置当前节点的前驱节点
if (node.getLeft() == null) {
//设置当前节点的前驱节点
node.setLeft(pre);
//设置当前节点的类型
node.setLeftType(1);
}
//2.设置后继节点
if (pre != null && pre.getRight() == null) {
//设置上一个节点的后继节点
pre.setRight(node);
//设置后继节点的类型
pre.setRightType(1);
}
//当前节点成为下一个节点的前驱节点
pre = node;
}
/**
* 按照【后序遍历】的方式遍历线索化二叉树
*/
public void postThreadList() {
HeroNode curNode = root;//设置一个临时变量,作为当前节点,从根节点开始
while (curNode.getLeftType() == 0) {//找到最左边的开始节点
curNode = curNode.getLeft();
}
HeroNode preNode=null;
while (curNode != null) {
//右边是线索
if(curNode.getRightType()==1){
System.out.println(curNode);
preNode=curNode;
curNode=curNode.getRight();
}else {
if(curNode.getRight()==preNode){//如果上个处理的节点是当前节点的右子节点
System.out.println(curNode);
if(curNode==root)
return;
preNode=curNode;
curNode=curNode.getParent();
}else {//如果从左节点的进入则找到有右子树的最左节点
curNode=curNode.getRight();
while (curNode!=null&&curNode.getLeftType()==0){
curNode=curNode.getLeft();
}
}
}
}
}
线索化部分完整代码:
/**
* @author Wnlife
* @create 2019-11-29 15:52
* <p>
* 线索化二叉树
*/
public class ThreadBinaryTreeDemo {
public static void main(String[] args) {
//测试一把中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
// HeroNode node7 = new HeroNode(17, "ddpp");
//二叉树,后面我们要递归创建, 现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node2.setParent(root);
node3.setLeft(node6);
node3.setParent(root);
node4.setParent(node2);
node5.setParent(node2);
node6.setParent(node3);
// node3.setRight(node7);
//测试中序线索化
ThreadBinaryTree tree = new ThreadBinaryTree(root);
// tree.infexThreadedNodes();
// HeroNode leftNode = node5.getLeft();
// HeroNode rightNode = node5.getRight();
// System.out.println("10号结点的前驱结点是 =" + leftNode); //3
// System.out.println("10号结点的后继结点是=" + rightNode); //1
// System.out.println("按照中序遍历,使用线索化的方式遍历 线索化二叉树");
// tree.infixThreadedList();// 8, 3, 10, 1, 14, 6
//测试前序线索化
// tree.preThreadedNodes();
// HeroNode leftNode = node4.getLeft();
// HeroNode rightNode = node4.getRight();
// System.out.println("8号结点的前驱结点是 =" + leftNode);//3
// System.out.println("8号结点的后继结点是=" + rightNode);//10
// System.out.println("按照前序遍历,使用线索化的方式遍历 线索化二叉树");
// tree.preThreadedList();//1 3 8 10 6 14
//测试后序线索化
tree.postThreadedNodes();
HeroNode leftNode = node6.getLeft();
HeroNode rightNode = node6.getRight();
System.out.println("14号结点的前驱结点是 =" + leftNode);//3
System.out.println("14号结点的后继结点是=" + rightNode);//6
System.out.println("按照后序遍历,使用线索化的方式遍历 线索化二叉树");
tree.postThreadList();//8 10 3 14 6 1
}
}
/**
* 线索化二叉树
*/
class ThreadBinaryTree {
//根节点
private HeroNode root;
//当前节点的前驱节点指针,在递归进行线索化时,pre总是保留前一个节点
private HeroNode pre;
public ThreadBinaryTree(HeroNode root) {
this.root = root;
}
public void infexThreadedNodes() {
infexThreadedNodes(root);
}
/**
* 按照【中序遍历】的顺序对二叉树进行线索化的方法
*
* @param node 当前需要线索化的节点
*/
public void infexThreadedNodes(HeroNode node) {
//一、当前节点为空,则不要进行线索化
if (node == null) {
return;
}
//二、先线索化左子节点
infexThreadedNodes(node.getLeft());
//线索化当前节点
//1.先处理当前节点的前驱节点
if (node.getLeft() == null) {
//让当前节点的左指针指向前驱节点
node.setLeft(pre);
//修改当前节点的左指针类型,指向前驱节点
node.setLeftType(1);
}
//2.处理后继节点
if (pre != null && pre.getRight() == null) {
//让前驱节点的右指针指向当前节点
pre.setRight(node);
//修改当前前驱节点的右指针类型
pre.setRightType(1);
}
pre = node;//当前节点都是下一个前驱节点
//三、线索化右子节点
infexThreadedNodes(node.getRight());
}
/**
* 按照【中序遍历】的方式进行线索化遍历二叉树
*/
public void infixThreadedList() {
HeroNode curNode = root;//定义一个变量,存储当前遍历的结点,从root开始
while (curNode != null) {
/**
* 找到中序遍历线索化二叉树时的第一个节点,
* 循环的找到leftType==1的节点,第一个找到的就是8节点,
* 后面随着遍历而变化,因为当leftType==1,说明该节点是按照线索化处理后的有效节点
*/
while (curNode.getLeftType() == 0) {
curNode = curNode.getLeft();
}
//打印出当前这个节点
System.out.println(curNode);
//如果当前节点的都是指向的都是后继节点,就一直输出
while (curNode.getRightType() == 1) {
//获取当前节点的后继节点
curNode = curNode.getRight();
System.out.println(curNode);
}
//替换这个遍历的节点
curNode = curNode.getRight();
}
}
public void preThreadedNodes() {
preThreadedNodes(root);
}
/**
* 按照【前序遍历】的方式线索化二叉树
*
* @param node 当前需要线索化的节点
*/
public void preThreadedNodes(HeroNode node) {
//一、如果当前节点为空,则直接返回
if (node == null) {
return;
}
//二、先线索化当前节点
//1.设置当前节点的前驱节点
if (node.getLeft() == null) {
//设置当前节点的前驱节点
node.setLeft(pre);
//设置当前节点的类型
node.setLeftType(1);
}
//2.设置后继节点
if (pre != null && pre.getRight() == null) {//1 3 8 10 6 14
//设置上一个节点的后继节点
pre.setRight(node);
//设置后继节点的类型
pre.setRightType(1);
}
//当前节点成为下一个节点的前驱节点
pre = node;
//三、线索化当前节点的左子树
if (node.getLeftType() != 1) {
preThreadedNodes(node.getLeft());
}
//四、线索化当前节点的右子树
if (node.getRightType() != 1) {
preThreadedNodes(node.getRight());
}
}
/**
* 按照【前序遍历】的方式遍历线索化二叉树
*/
public void preThreadedList() {
HeroNode curNode = root;//定义一个变量,存储当前遍历的结点,从root开始
while (curNode != null) {
//遇到先对其进行进行访问,再对其左子树进行遍历访问,直到找到最左的那个节点;
while (curNode.getLeftType() == 0) {
System.out.println(curNode);
curNode = curNode.getLeft();
}
//再根据线索化的指向对其右子树进行遍历访问。
System.out.println(curNode);
curNode = curNode.getRight();
}
}
public void postThreadedNodes() {
postThreadedNodes(root);
}
/**
* 按照【后序遍历】的方式线索化二叉树
*
* @param node 当前需要线索化的节点
*/
public void postThreadedNodes(HeroNode node) {
//一、如果当前节点为空,则直接返回
if (node == null) {
return;
}
//二、线索化当前节点的左子树
postThreadedNodes(node.getLeft());
//三、线索化当前节点的右子树
postThreadedNodes(node.getRight());
//四、先线索化当前节点
//1.设置当前节点的前驱节点
if (node.getLeft() == null) {
//设置当前节点的前驱节点
node.setLeft(pre);
//设置当前节点的类型
node.setLeftType(1);
}
//2.设置后继节点
if (pre != null && pre.getRight() == null) {
//设置上一个节点的后继节点
pre.setRight(node);
//设置后继节点的类型
pre.setRightType(1);
}
//当前节点成为下一个节点的前驱节点
pre = node;
}
/**
* 按照【后序遍历】的方式遍历线索化二叉树
*/
public void postThreadList() {
HeroNode curNode = root;//设置一个临时变量,作为当前节点,从根节点开始
while (curNode.getLeftType() == 0) {//找到最左边的开始节点
curNode = curNode.getLeft();
}
HeroNode preNode=null;
while (curNode != null) {
//右边是线索
if(curNode.getRightType()==1){
System.out.println(curNode);
preNode=curNode;
curNode=curNode.getRight();
}else {
if(curNode.getRight()==preNode){//如果上个处理的节点是当前节点的右子节点
System.out.println(curNode);
if(curNode==root)
return;
preNode=curNode;
curNode=curNode.getParent();
}else {//如果从左节点的进入则找到有右子树的最左节点
curNode=curNode.getRight();
while (curNode!=null&&curNode.getLeftType()==0){
curNode=curNode.getLeft();
}
}
}
}
}
}
/**
* 创建HeroNode节点
*/
class HeroNode {
private int no;
private String name;
private HeroNode left;
private HeroNode right;
//这只父节点,在后序线索化遍历时使用
private HeroNode parent;
/**
* 说明:
* 1.如果leftType==0,表示是左子树,如果是1表示是前驱节点
* 2.如果rightType==0,表示是右子树,如果是1表示是后继节点
*/
private int leftType;
private int rightType;
public void setParent(HeroNode parent) {
this.parent = parent;
}
public HeroNode getParent() {
return parent;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public int getLeftType() {
return leftType;
}
public int getRightType() {
return rightType;
}
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public String getName() {
return name;
}
public HeroNode getLeft() {
return left;
}
public HeroNode getRight() {
return right;
}
public void setNo(int no) {
this.no = no;
}
public void setName(String name) {
this.name = name;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}
2树结构实际应用
2.1堆排序
2.1.1对排序基本介绍
- 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
- 堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
- 大顶堆举例说明:
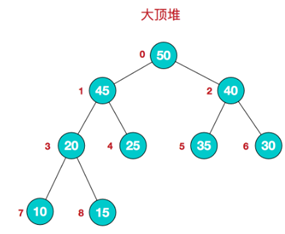
我们对堆中的结点按层进行编号,映射到数组中就是下面这个样子:

大顶堆特点:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] // i 对应第几个节点,i从0开始编号 - 小顶堆举例说明
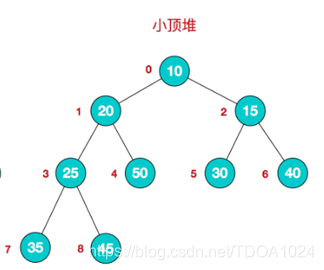
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] // i 对应第几个节点,i从0开始编号 - 一般升序采用大顶堆,降序采用小顶堆
2.1.2堆排序基本思想
堆排序的基本思想是:
- 将待排序序列构造成一个大顶堆
- 此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
- 可以看到在构建大顶堆的过程中,元素的个数逐渐减少,最后就得到一个有序序列了.
2.1.3堆排序步骤图解说明
要求:给你一个数组 {4,6,8,5,9} , 要求使用堆排序法,将数组升序排序。
堆排序思路和步骤图解:
- 步骤一:构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
1)假设给定无序序列结构如下
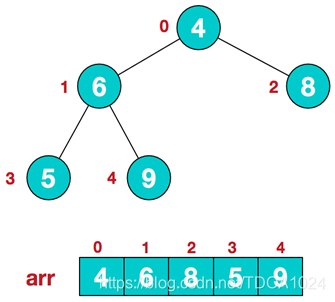
2)此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
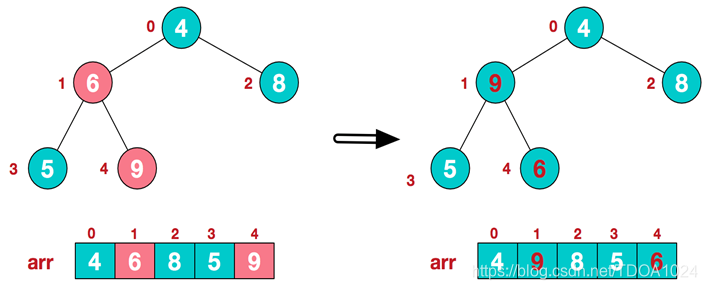
3)找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
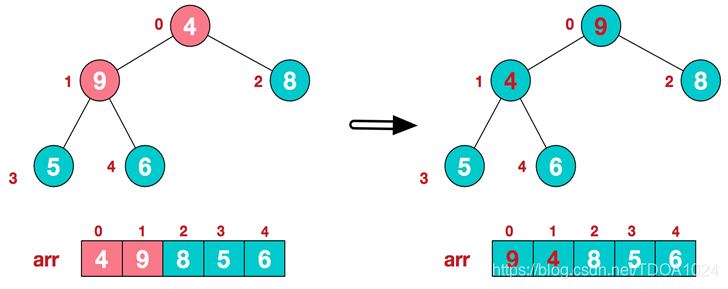
- 这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
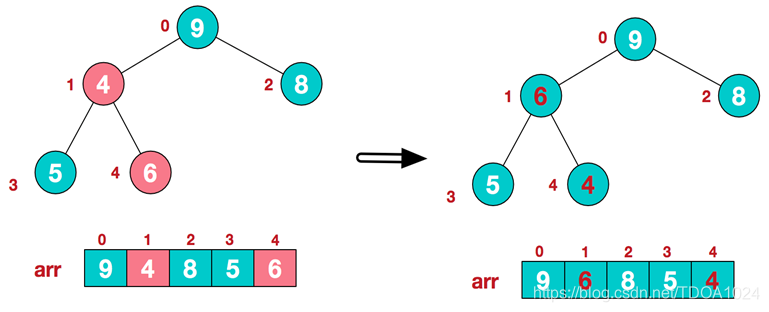
此时,我们就将一个无序序列构造成了一个大顶堆。
- 步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
1)将堆顶元素9和末尾元素4进行交换

2)重新调整结构,使其继续满足堆定义
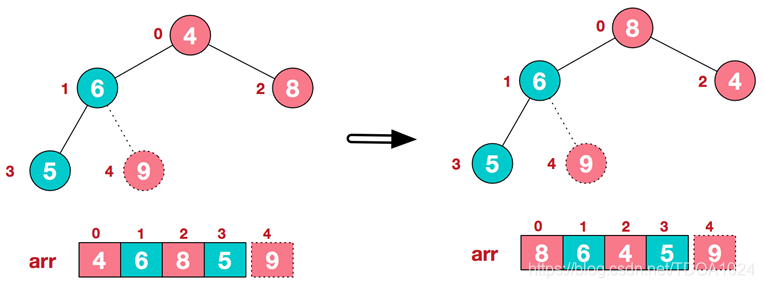
3)再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
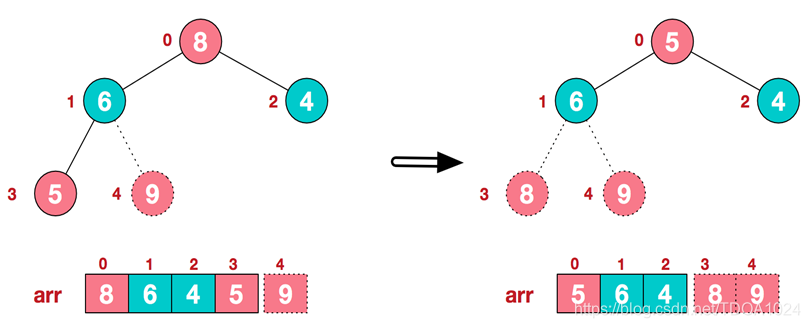
- 后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序。
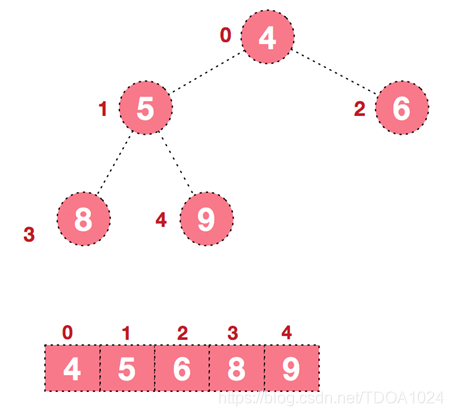
- 再简单总结下堆排序的基本思路:
- 将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
- 将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
- 重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
2.1.4堆排序代码实现
要求:给你一个数组 {4,6,8,5,9} , 要求使用堆排序法,将数组升序排序。
代码实现:
/**
* @author Wnlife
* @create 2019-12-05 21:36
* 堆排序
*/
public class HeapSort {
public static void main(String[] args) {
// int[] arr = {4, 6, 8, 5, 9, -8, 50, -34, 65};
int[]arr=new int[8000000];
for (int i = 0; i <8000000; i++) {
arr[i]=(int) Math.random()*8000000;
}
System.out.println("排序前:");
Instant now1 = Instant.now();
heapSort(arr);
Instant now2 = Instant.now();
// System.out.println(Arrays.toString(arr));
System.out.println("排序的时间是:"+Duration.between(now1,now2).toMillis());
}
/**
* 堆排序算法
*
* @param arr 待排序的数组
*/
public static void heapSort(int[] arr) {
int temp = 0;
//1).将一个无序的数组变为一个堆,根据升序降序需求选择大顶堆或小顶堆
for (int i = arr.length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, arr.length);
}
/**
* 2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
* 3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,
* 反复执行调整+交换步骤,直到整个序列有序。
*/
for (int j = arr.length - 1; j > 0; j--) {
temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
adjustHeap(arr, 0, j);
}
}
/**
* 将一个数组(二叉树),调整为一个大堆顶
* 功能:将 以 i 对应的非叶子结点的树调整成大顶堆
* 举例:int arr[] = {4, 6, 8, 5, 9}; i=1 -> adjustHeap -> 得到 {4, 9, 8, 5, 6}
* 如果再次调用adjustHeap,传入的是 i = 0 -> 得到 {4, 9, 8, 5, 6} -> {9,6,8,5, 4}
*
* @param arr 要调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length 是在逐渐的减少
*/
public static void adjustHeap(int[] arr, int i, int length) {
int temp = arr[i];//保存当前节点的值
//k = 2*i+1是当前节点的左子节点
for (int k = 2 * i + 1; k < length; k = k * 2 + 1) {
if (k + 1 < length && arr[k] < arr[k + 1]) {//说明右子节点大于左子节点的值
k++;
}
if (arr[k] > temp) {//如果子节点大于父节点
arr[i] = arr[k];//将比较大的子节点的值和当前节点的值互换
i = k;//循环向下比较
} else {
break;
}
}
//循环结束后,已经将当前的子树的最大值放在顶部
arr[i] = temp; // 将temp的值赋值给调整后的位置
}
}
2.2赫夫曼树
2.2.1基本介绍
- 给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为赫夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
- 赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
2.2.2赫夫曼树几个重要概念和举例说明
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
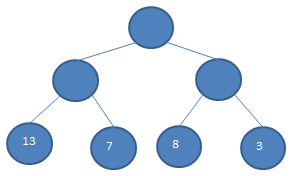
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
- WPL最小的就是赫夫曼树。
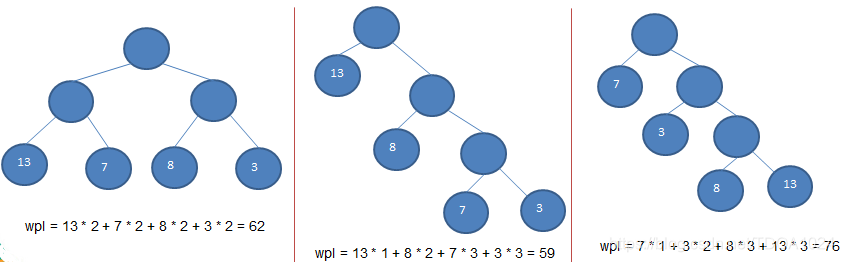
2.2.3赫夫曼树创建思路图解
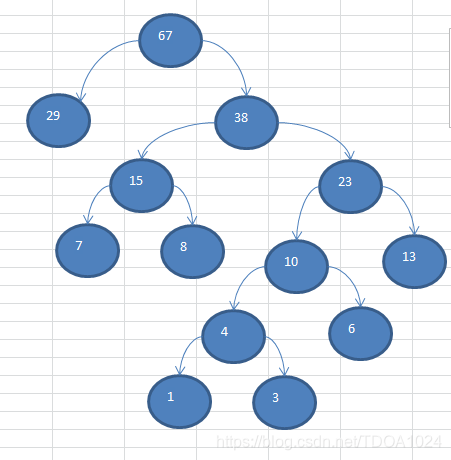
给你一个数列 {13, 7, 8, 3, 29, 6, 1},要求转成一颗赫夫曼树.
思路分析(示意图):
{13, 7, 8, 3, 29, 6, 1}
构成赫夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树
2.2.4赫夫曼树的代码实现
/**
* @author Wnlife
* @create 2019-12-06 16:14
* <p>
* 实现赫夫曼树
*/
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
preOrder(root);
}
/**
* 前序遍历
* @param root 要遍历的树的根节点
*/
public static void preOrder(Node root){
if(root!=null){
root.preOrder();
}else {
System.out.println("此树是空树,不能遍历~~");
}
}
/**
* 创建赫夫曼树
* @param arr 需要创建成哈夫曼树的数组
* @return 创建好的赫夫曼树的根节点
*/
public static Node createHuffmanTree(int[]arr){
/*
*第一步:遍历数组,将arr数组中每一个元素构成一个Node,将每一个Node放入到ArrayList中
*/
List<Node> nodes = new ArrayList<>();
for (int val : arr) {
nodes.add(new Node(val));
}
//循环处理
while (nodes.size()>1){
Collections.sort(nodes);//排序,从小到大
//取出根节点权值最小的两颗儿茶素
Node leftNode=nodes.get(0);//取出权值最小的节点
Node rightNode=nodes.get(1);//取出权值第二小的节点
//将取出的两个节点构造为一颗新的二叉树
Node node = new Node(leftNode.value + rightNode.value);
node.left=leftNode;
node.right=rightNode;
//从集合中删除取出的节点
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新节点添加到集合中
nodes.add(node);
}
return nodes.get(0);
}
}
/**
* 树节点
*/
class Node implements Comparable<Node>{
int value;//节点权值
Node left;//指向左子节点
Node right;//指向右子节点
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
@Override
public int compareTo(Node o) {
// 表示从小到大排序
return this.value-o.value;
}
}
2.3赫夫曼编码
2.3.1基本介绍
- 赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
- 赫夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 赫夫曼编码广泛地用于数据文件压缩。其压缩率通常在20%~90%之间
- 赫夫曼码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,称之为最佳编码
2.3.2原理剖析
- 通信领域中信息的处理方式1-定长编码
i like like like java do you like a java // 共40个字符(包括空格)
105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106 97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97 118 97 //对应Ascii码
01101001 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101100 01101001 01101011 01100101 00100000 01101010 01100001 01110110 01100001 00100000 01100100 01101111 00100000 01111001 01101111 01110101 00100000 01101100 01101001 01101011 01100101 00100000 01100001 00100000 01101010 01100001 01110110 01100001 //对应的二进制
按照二进制来传递信息,总的长度是 359 (包括空格)
在线转码 工具 :https://www.mokuge.com/tool/asciito16/
- 通信领域中信息的处理方式2-变长编码
i like like like java do you like a java // 共40个字符(包括空格)
d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数
0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u, 1010=y, 1011=d 说明:按照各个字符出现的次数生成一个编码表,原则是出现次数越多的,则编码越小,比如 空格出现了9 次, 编码为0 ,其它依次类推.
按照上面给各个字符规定的编码,则我们在传输 “i like like like java do you like a java” 数据时,编码就是 10010110100…
字符的编码都不能是其他字符编码的前缀,符合此要求的编码叫做前缀编码, 即不能匹配到重复的编码.
- 通信领域中信息的处理方式3-赫夫曼编码
传输的 字符串
- i like like like java do you like a java
- d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各个字符对应的个数
- 按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
步骤:
构成赫夫曼树的步骤:- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树
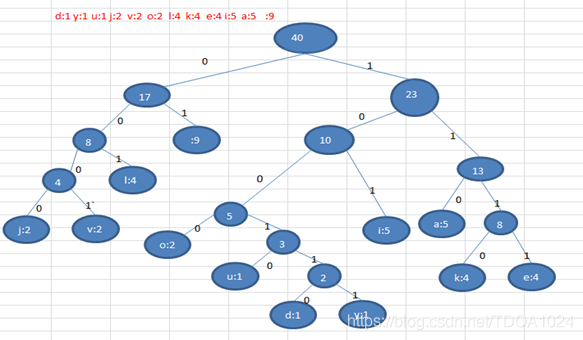
- 根据赫夫曼树,给各个字符,规定编码 (前缀编码), 向左的路径为0 向右的路径为1 , 编码如下:
o: 1000 u: 10010 d: 100110 y: 100111 i: 101
a : 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 : 01 - 按照上面的赫夫曼编码,我们的"i like like like java do you like a java" 字符串对应的编码为 (注意这里我们使用的无损压缩)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110 通过赫夫曼编码处理 长度为 133 - 长度为 : 133
说明:
原来长度是 359 , 压缩了 (359-133) / 359 = 62.9%
此编码满足前缀编码, 即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性
赫夫曼编码是无损处理方案
- 注意事项
注意, 这个赫夫曼树根据排序方法不同,也可能不太一样,这样对应的赫夫曼编码也不完全一样,但是wpl 是一样的,都是最小的, 最后生成的赫夫曼编码的长度是一样的。比如: 如果我们让每次生成的新的二叉树总是排在权值相同的二叉树的最后一个,则生成的二叉树为:

2.2.3最佳实践-数据压缩(创建赫夫曼树)
将给出的一段文本,比如 “i like like like java do you like a java” , 根据前面的讲的赫夫曼编码原理,对其进行数据压缩处理 ,形式如 1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
步骤1:根据赫夫曼编码压缩数据的原理,需要创建 “i like like like java do you like a java” 对应的赫夫曼树.
步骤2:生成赫夫曼树对应的赫夫曼编码 , 如下表:=01 a=100 d=11000 u=11001 e=1110 v=11011 i=101 y=11010 j=0010 k=1111 l=000 o=0011
步骤3:使用赫夫曼编码来生成赫夫曼编码数据 ,即按照上面的赫夫曼编码,将"i like like like java do you like a java" 字符串生成对应的编码数据, 形式如下.
1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
2.2.4最佳实践-数据解压(使用赫夫曼编码解码)
使用赫夫曼编码来解码数据,具体要求是
前面我们得到了赫夫曼编码和对应的编码 byte[] , 即:[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
现在要求使用赫夫曼编码, 进行解码,又重新得到原来的字符串"i like like like java do you like a java"
2.2.5 最佳实践-文件压缩
我们学习了通过赫夫曼编码对一个字符串进行编码和解码, 下面我们来完成对文件的压缩和解压, 具体要求:给你一个图片文件,要求对其进行无损压缩, 看看压缩效果如何。
思路:读取文件-> 得到赫夫曼编码表 -> 完成压缩
2.2.6 最佳实践-文件解压(文件恢复)
具体要求:将前面压缩的文件,重新恢复成原来的文件。
思路:读取压缩文件(数据和赫夫曼编码表)-> 完成解压(文件恢复)
2.2.7 整体赫夫曼编码代码
import java.io.*;
import java.util.*;
/**
* @author Wnlife
* @create 2019-12-07 16:34
* <p>
* 赫夫曼编码
*/
public class HuffmanCode {
public static void main(String[] args) {
/* String content = "i like like like java do you like a java";
System.out.println("要编码的字符串为:" + content);
byte[] bytes = content.getBytes();
System.out.println("要编码的字节数组:" + Arrays.toString(bytes) + "长度为:" + bytes.length);
List<Node> nodes = getNodes(bytes);//生成对应 的节点集合
System.out.println("生成的节点集合:" + nodes);
Node root = createHuffmanTree(nodes);//生成赫夫曼树
System.out.println("前序遍历:");
preOrder(root);//前序遍历观察
getCodes(root);//获取编码
System.out.println(huffmanCodes);
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);//生成编码后的字节数组
System.out.println("编码后的字节数组:"+Arrays.toString(huffmanCodeBytes));
byte[] huffmanCodeBytes = huffmanZip(bytes);
System.out.println("压缩后的字节数组:" + Arrays.toString(huffmanCodeBytes) + "长度为:" + huffmanCodeBytes.length);
byte[] decodeBytes = decode(huffmanCodes, huffmanCodeBytes);
System.out.println("解码后的数据为:" + new String(decodeBytes));*/
//文件压缩测试
// zipFile("E:\\0.bmp", "E:\\1.zip");
// System.out.println("压缩文件完成~~");
//文件解压测试
unZipFile("E:\\1.zip","E:\\1.bmp");
System.out.println("解压文件完成~~");
}
/************************************************************文件压缩与解压**********************************************************/
/**
* 编写一个方法,完成对压缩文件的解压
* @param zipFile 要解压的文件的路径
* @param dstFile 解压后的文件存放路径
*/
public static void unZipFile(String zipFile, String dstFile) {
//创建输入流
ObjectInputStream ois = null;
//创建输出流
FileOutputStream os = null;
try {
//将要解压的文件读入到流中
ois = new ObjectInputStream(new FileInputStream(zipFile));
//从流中读取编码后的字节数组huffmanBytes
byte[] huffmanBytes = (byte[]) ois.readObject();
//从流中读取赫夫曼编码表
Map<Byte, String> huffmanCodes = (Map<Byte, String>) ois.readObject();
//解码
byte[] bytes = decode(huffmanCodes, huffmanBytes);
//将bytes 数组写入到目标文件
os = new FileOutputStream(dstFile);
os.write(bytes);
} catch (Exception e) {
e.printStackTrace();
} finally {
try {
ois.close();
os.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
/**
* 将一个文件使用赫夫曼编码进行压缩
*
* @param srcFile 需要压缩的文件目录
* @param dstFile 压缩后文件存放的目录
*/
public static void zipFile(String srcFile, String dstFile) {
//创建输出流
ObjectOutputStream oos = null;
//创建为文件输入的流
FileInputStream is = null;
try {
//将文件读入到刘中
is = new FileInputStream(srcFile);
byte[] bytes = new byte[is.available()];
//把文件读到字节数组中
is.read(bytes);
//对文件进行赫夫曼压缩
byte[] huffmanBytes = huffmanZip(bytes);
//创建文件输出流,存放压缩的文件
oos = new ObjectOutputStream(new FileOutputStream(dstFile));
//把 赫夫曼编码后的字节数组写入压缩文件
oos.writeObject(huffmanBytes);
//以对象流的方式写入赫夫曼编码,是为了以后我恢复源文件时使用,一定要把赫夫曼编码写入到压缩文件
oos.writeObject(huffmanCodes);
} catch (Exception e) {
e.printStackTrace();
} finally {
try {
oos.close();
is.close();
} catch (IOException e) {
e.printStackTrace();
}
}
}
/*******************************************************解码***********************************************************/
/**
* 根绝赫夫曼编码表,对数据压缩的数据进行解压
* 思路:
* 1. 将huffmanCodeBytes [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
* 重写先转成 赫夫曼编码对应的二进制的字符串 "1010100010111..."
* 2. 赫夫曼编码对应的二进制的字符串 "1010100010111..." =》 对照 赫夫曼编码 =》 "i like like like java do you like a java"
*
* @param huffmanCodes 赫夫曼编码表
* @param huffmanBytes 赫夫曼编码后的字节数组
* @return 解码后的byte数组
*/
public static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {
//得到huffmanBytes对应的二进制字符串,形式101010001011111111...
StringBuilder sb = new StringBuilder();
for (int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
boolean flag = (i == huffmanBytes.length - 1);
sb.append(byteToBitString(!flag, b));
}
//把赫夫曼编码表进行反向调换,因为需要反向查询
Map<String, Byte> map = new HashMap<>();
for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//把得到的字符串根据反向的赫夫曼编码表进行解码
List<Byte> list = new ArrayList<>();//存放解码后的byte
//扫描sb字符串,对每个匹配到的二进制字符串进行解码
for (int i = 0; i < sb.length(); ) {
int count = 1;
Byte b = null;
boolean flag = true;
while (flag) {
String key = sb.substring(i, i + count);//i 不动,让count移动,指定匹配到一个字符
b = map.get(key);
if (b == null) {//没有匹配到
count++;
} else {//匹配到
flag = false;
}
}
i += count;
list.add(b);
}
//当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java"
//把list 中的数据放入到byte[] 并返回
byte[] bytes = new byte[list.size()];
for (int i = 0; i < list.size(); i++) {
bytes[i] = list.get(i);
}
return bytes;
}
/**
* 将一个byte转成其对应的二进制的字符串
*
* @param flag 标志是否需要补高位如果是true ,表示需要补高位,如果是false表示不补, 如果是最后一个字节,无需补高位
* @param b 传入的byte
* @return 是传入的b对应的二进制字符串(注意是按照补码返回)
*/
public static String byteToBitString(boolean flag, byte b) {
//将b转成int类型
int temp = b;
//如果是正数,需要补高位
if (flag) {
temp |= 256;
}
String str = Integer.toBinaryString(temp);//返回的是temp对应的二进制的补码
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
/*******************************************************编码***********************************************************/
/**
* 赫夫曼编码
*
* @param bytes 要编码的字节数组
* @return 编码后的字节数组
*/
public static byte[] huffmanZip(byte[] bytes) {
//生成对应 的节点集合
List<Node> nodeList = getNodes(bytes);
//生成赫夫曼树
Node root = createHuffmanTree(nodeList);
//获取编码表
getCodes(root);
//生成编码后的字节数组
byte[] huffmanCodeBytes = zip(bytes, huffmanCodes);
return huffmanCodeBytes;
}
/**
* 根据所生成的哈夫曼编码表,对传入的字节数组进行编码,返回编码后的字节数组
*
* @param bytes 要编码的字节数组
* [105, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 106, 97,
* 118, 97, 32, 100, 111, 32, 121, 111, 117, 32, 108, 105, 107, 101, 32, 97, 32, 106, 97, 118, 97]
* @param huffmanCodes 赫夫曼编码表
* @return 编码后的字节数组
* [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
*/
public static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
StringBuilder sb = new StringBuilder();
//根据编码表对传入的字节数组进行编码,生成一个编码后的字符串
//101010001011111111001000101111111100100010111111110010010100110111000111000001101
// 1101000111100101000101111111100110001001010011011100
for (byte b : bytes) {
sb.append(huffmanCodes.get(b));
}
// System.out.println(sb.toString());
/**
* 将编码后的二进制字符串每8位变为一个字节(byte),放入到一个字节数组中huffmanCodeBytes
* 例子:
* 前8位:10101000(补码)->10101000 - 1 =10100111(反码)->11011000=-88
*/
//计算最后生成的字节数组的长度
int len;
if (sb.length() % 8 == 0) {
len = sb.length() / 8;
} else {
len = sb.length() / 8 + 1;
}
//创建压缩后的子节数组的长度
byte[] huffmanCodeBytes = new byte[len];
int index = 0;
for (int i = 0; i < sb.length(); i += 8) {
String strByte;
if (i + 8 > sb.length()) {
strByte = sb.substring(i);
} else {
strByte = sb.substring(i, i + 8);
}
//将strByte转成一个byte,放入到huffmanCodeBytes中
huffmanCodeBytes[index++] = (byte) Integer.parseInt(strByte, 2);
}
return huffmanCodeBytes;
}
/**
* 生成对应的赫夫曼编码表:
*/
static Map<Byte, String> huffmanCodes = new HashMap<Byte, String>();
// 在生成赫夫曼编码表示,需要去拼接路径, 定义一个StringBuilder 存储某个叶子结点的路径
static StringBuilder stringBuilder = new StringBuilder();
public static void getCodes(Node root) {
if (root == null) {
return;
}
//处理哈夫曼树的左子节点
getCodes(root.left, "0", stringBuilder);
//处理哈夫曼树的右子节点
getCodes(root.right, "1", stringBuilder);
}
/**
* 将传入的node节点的hehuman编码存入到map中,形成一个赫夫曼编码表
* {32=01, 97=100, 100=11000, 117=11001, 101=1110, 118=11011, 105=101, 121=11010, 106=0010, 107=1111, 108=000, 111=0011}
*
* @param node 传入的节点
* @param code 路径: 左子结点是 0, 右子结点 1
* @param sb 用于拼接路径
*/
public static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
if (node != null) {//node为空不处理
//判断当前节点是叶子节点还是非叶子节点
if (node.data == null) {//非叶子节点
//向左递归处理
getCodes(node.left, "0", sb2);
//向右递归处理
getCodes(node.right, "1", sb2);
} else {//是叶子节点,表示找到某个叶子节点的最后
huffmanCodes.put(node.data, sb2.toString());
}
}
}
/**
* 前序遍历的方法
*
* @param root 树的根节点
*/
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("赫夫曼树为空");
}
}
/**
* 可以通过List创建对应的赫夫曼树
*
* @param nodes
* @return
*/
public static Node createHuffmanTree(List<Node> nodes) {
while (nodes.size() > 1) {
//先对原先的集合进行排序
Collections.sort(nodes);
//取出第一课最小的二叉树
Node leftNode = nodes.get(0);
//取出第二颗最小的二叉树
Node rightNode = nodes.get(1);
//创建一颗新的二叉树,它的根节点 没有data, 只有权值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已处理的两颗二叉树从集合中删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉树添加到集合中
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 将要编码的字符串对应的字节数组变成一个Node节点的List集合,统计每个字符出现的次数
*
* @param bytes 要编码的字符串对应的字节数组
* @return Node节点的List集合
*/
public static List<Node> getNodes(byte[] bytes) {
List<Node> list = new ArrayList<>();
Map<Byte, Integer> byteCounts = new HashMap<>();
//统计每个字符出现的次数,放入到map中
for (byte b : bytes) {
Integer count = byteCounts.get(b);
if (count == null) {
byteCounts.put(b, 1);
} else {
byteCounts.put(b, count + 1);
}
}
//将map中的元素转换为Node并存入到List中
for (Map.Entry<Byte, Integer> entry : byteCounts.entrySet()) {
list.add(new Node(entry.getKey(), entry.getValue()));
}
return list;
}
}
/**
* 树的节点
*/
class Node implements Comparable<Node> {
Byte data;//存放数据本身,比如'a' => 97 ,' ' => 32
int weight;//权重,表示字符出现的次数
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
@Override
public int compareTo(Node o) {
return this.weight - o.weight;//从小到排序
}
/**
* 前序遍历
*/
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
2.2.8赫夫曼编码压缩文件注意事项
- 如果文件本身就是经过压缩处理的,那么使用赫夫曼编码再压缩效率不会有明显变化, 比如视频,ppt 等等文件 [举例压一个 .ppt]
- 赫夫曼编码是按字节来处理的,因此可以处理所有的文件(二进制文件、文本文件) [举例压一个.xml文件]
- 如果一个文件中的内容,重复的数据不多,压缩效果也不会很明显.
2.2.9赫夫曼编码代码的关键问题细节补充
代码1: 赫夫曼编码代码
/**
* 根据所生成的哈夫曼编码表,对传入的字节数组进行编码,返回编码后的字节数组
*
* @param bytes 要编码的字节数组
* [105, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 106, 97,
* 118, 97, 32, 100, 111, 32, 121, 111, 117, 32, 108, 105, 107, 101, 32, 97, 32, 106, 97, 118, 97]
* @param huffmanCodes 赫夫曼编码表
* @return 编码后的字节数组
* [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
*/
public static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) {
StringBuilder sb = new StringBuilder();
//根据编码表对传入的字节数组进行编码,生成一个编码后的字符串
//101010001011111111001000101111111100100010111111110010010100110111000111000001101
// 1101000111100101000101111111100110001001010011011100
for (byte b : bytes) {
sb.append(huffmanCodes.get(b));
}
/**
* 将编码后的二进制字符串每8位变为一个字节(byte),放入到一个字节数组中huffmanCodeBytes
* 例子:前8位:10101000(补码)->10101000 - 1 =10100111(反码)->11011000=-88
*/
//计算最后生成的字节数组的长度: lem=(sb.length()+7)/8;
int len;
if (sb.length() % 8 == 0) {
len = sb.length() / 8;
} else {
len = sb.length() / 8 + 1;
}
//创建压缩后的子节数组的长度
byte[] huffmanCodeBytes = new byte[len];
int index = 0;
for (int i = 0; i < sb.length(); i += 8) {
String strByte;
if (i + 8 > sb.length()) {
strByte = sb.substring(i);
} else {
strByte = sb.substring(i, i + 8);
}
huffmanCodeBytes[index++] = (byte) Integer.parseInt(strByte, 2);
}
return huffmanCodeBytes;
}
方法详解
- 方法的目的: 根据所生成的哈夫曼编码表,对传入的原始字节数组进行编码,返回编码后的字节数组
- 传入的字节数组:
[105, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 106, 97,118, 97, 32, 100, 111, 32, 121, 111, 117, 32, 108, 105, 107, 101, 32, 97, 32, 106, 97, 118, 97]
- 先转成对应的二进制字符串
1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
- 根据赫夫曼编码表转成编码后的字节数组:
[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
- 方法的执行细节:
- 将传入的原始字节数组 根据赫夫曼编码表进行编码,得到一组二进制字符串:
StringBuilder sb = new StringBuilder(); for (byte b : bytes) { sb.append(huffmanCodes.get(b)); }- 二进制字符串:
1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
- 将编码后的二进制字符串每8位变为一个字节(byte),放入到一个字节数组中huffmanCodeBytes
例子:前8位:10101000(补码)->10101000 - 1 =10100111(反码)->11011000(原码)=-88,将每8个长度的二进制字符串当做一个字节的补码,将补码(计算机内部使用的都是补码)通过转换变成原码,进而转换为其对应的byte。
//计算最后生成的字节数组的长度: lem=(sb.length()+7)/8; int len; if (sb.length() % 8 == 0) { len = sb.length() / 8; } else { len = sb.length() / 8 + 1; } //创建压缩后的子节数组的长度 byte[] huffmanCodeBytes = new byte[len];- 正式进行转换,将每8位二进制字符串转换为一个byte
int index = 0; for (int i = 0; i < sb.length(); i += 8) { String strByte;//截取后的字符串 if (i + 8 > sb.length()) {//防止截取最后一段字符串时数组越界 strByte = sb.substring(i); } else { strByte = sb.substring(i, i + 8); } huffmanCodeBytes[index++] = (byte) Integer.parseInt(strByte, 2); } return huffmanCodeBytes;- 详解:huffmanCodeBytes[index++] = (byte) Integer.parseInt(strByte, 2)
目的:将strByte转成一个byte,即每8个切割后的二进制字符串转成一个byte,放入到huffmanCodeBytes中
计算机存储的都是补码,现在想得到10101000对应的byte,即对应的原码,可以使用Integer类中的parseInt(String s, int radix)方法转换。
但是使用这个方法将8位的二进制字符串转换时,8位的二进制字符串是当做32位进行转换的(高位用0补齐),这就导致原本8位二进制字符串“10101000”最高位的1不再表示符号位,而32位二进制字符串最开头补上的0才是符号位,这样转换后得到的int类型不是我们对应的byte类型,但是转换后的int类型的后八位和我们需要的byte类型的后8位是一样的, 所以,可以直接使用类型转换截取后8位,得到我们想要的byte类型,即“10101000”对应的byte。
注意:使用Byte.parseInt()方法内部也是调用的 Integer.parseInt()方法,然后直接转换byte,截断最后8位。
代码2:赫夫曼解码
/**
* 根绝赫夫曼编码表,对数据压缩的数据进行解压
* 思路:
* 1. 将huffmanCodeBytes [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
* 重写先转成 赫夫曼编码对应的二进制的字符串 "1010100010111..."
* 2. 赫夫曼编码对应的二进制的字符串 "1010100010111..." -> 对照 赫夫曼编码 -> "i like like like java do you like a java"
*
* @param huffmanCodes 赫夫曼编码表
* @param huffmanBytes 赫夫曼编码后的字节数组
* @return 解码后的byte数组
*/
public static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) {
//得到huffmanBytes对应的二进制字符串,形式101010001011111111...
StringBuilder sb = new StringBuilder();
for (int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
boolean flag = (i == huffmanBytes.length - 1);
sb.append(byteToBitString(!flag, b));
}
//把赫夫曼编码表进行反向调换,因为需要反向查询
Map<String, Byte> map = new HashMap<>();
for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//把得到的字符串根据反向的赫夫曼编码表进行解码
List<Byte> list = new ArrayList<>();//存放解码后的byte
//扫描sb字符串,对每个匹配到的二进制字符串进行解码
for (int i = 0; i < sb.length(); ) {
int count = 1;
Byte b = null;
boolean flag = true;
while (flag) {
//i 不动,让count移动,指定匹配到一个字符
String key = sb.substring(i, i + count);
b = map.get(key);
if (b == null) {//没有匹配到
count++;
} else {//匹配到
flag = false;
}
}
i += count;
list.add(b);
}
//当for循环结束后,我们list中就存放了所有的字符
// "i like like like java do you like a java"
//把list 中的数据放入到byte[] 并返回
byte[] bytes = new byte[list.size()];
for (int i = 0; i < list.size(); i++) {
bytes[i] = list.get(i);
}
return bytes;
}
/**
* 将一个byte转成其对应的二进制的字符串
*
* @param flag 标志是否需要补高位,如果是true表示需要补高位,如果是false表示不补,
* 如果是最后一个字节,无需补高位(原因:因为最后一个字节对应编码后的二进制字符串的最后一段,
* 不一定长度为8,用256补完高位,这个字节对应的字符串长度会变为变成8,这是要不得的)
* @param b 传入的byte
* @return 是传入的b对应的二进制字符串(注意是按照补码返回)
*/
public static String byteToBitString(boolean flag, byte b) {
//将b转成int类型
int temp = b;
if (flag) {
temp |= 256;
}
String str = Integer.toBinaryString(temp);//返回的是temp对应的二进制的补码
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
- 方法目的:将编码后的字符串根据赫夫曼编码表解码为原始的字符串
- 传入的编码后的字节数组
[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28]
- 先转成对应的二进制字符串
1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
- 再根据反向赫夫曼编码表,每8个二进制字符串进行解码,得到原始字符窜的byte数组
[105, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 106, 97,118, 97, 32, 100, 111, 32, 121, 111, 117, 32, 108, 105, 107, 101, 32, 97, 32, 106, 97, 118, 97]
- 根据这个字节数组可以转成原始的字符串
- 方法的执行细节
- 预处理传入的编码后的字节数组,将其转为一串二进制字符串
StringBuilder sb = new StringBuilder(); for (int i = 0; i < huffmanBytes.length; i++) {//遍历字节数组 byte b = huffmanBytes[i]; boolean flag = (i == huffmanBytes.length - 1); sb.append(byteToBitString(!flag, b)); } - 将一个byte转为二进制字符串的方法
补高位问题:最后一个字节如果是正数,则需要补高位。/** * @param flag 标志是否需要补高位,如果是true表示需要补高位,如果是false表示不补, * @param b 传入的byte * @return 是传入的b对应的二进制字符串(注意是按照补码返回) */ public static String byteToBitString(boolean flag, byte b) { //将b转成int类型 int temp = b; //对最后一个之前的的byte补高位(正数才有必要补) if (flag) { temp |= 256; } String str = Integer.toBinaryString(temp);//返回的是temp对应的二进制的补码 if (flag) { return str.substring(str.length() - 8); } else { return str; } }
原因:如果是正数,使用Integer.toBinaryString()方法得到的是无前导0的二进制字符串,
得到的字符串可能长度小于8,而在编码是长度小于8的是以0占据的,所以此处使用temp |= 256,
temp | 1 0000 0000,将temp的高位补满0,在最后转换成字符串时,只截取8位,
因为我们在编码过程中,一直是用 byte=“8位二进制字符串” 一一对应的。
如果是最后一个字节,无需补高位 (原因:因为最后一个字节对应编码后的二进制字符串的最后一段,不一定长度为8,用256补完高位,这个字节对应的字符串长度会变为变成8,这跟编码时的二进制字符串是对不上的。)
Integer.toBinaryString(temp):在将byte转为int后(无损转换),需要使用一个方法把正数转换为对应的二进制字符串,就用到了这个方法,得到的是一个补码,因为一个字节对应的是8位二进制,int转成的二进制有32位,所以需要使用substring方法截取最后8位。最后一个字节不用截取,因为正数使用substring方法得到的二进制是无前导0的,不需要截取。 - 把赫夫曼编码表进行反向调换,因为需要反向查询
Map<String, Byte> map = new HashMap<>(); for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) { map.put(entry.getValue(), entry.getKey()); } - 把得到的字符串根据反向的赫夫曼编码表进行解码
List<Byte> list = new ArrayList<>();//存放解码后的byte //扫描sb字符串,对每个匹配到的二进制字符串进行解码 for (int i = 0; i < sb.length(); ) { int count = 1; Byte b = null; boolean flag = true; while (flag) { String key = sb.substring(i, i + count);//i 不动,让count移动,指定匹配到一个字符 b = map.get(key); if (b == null) {//没有匹配到 count++; } else {//匹配到 flag = false; } } i += count; list.add(b); } //当for循环结束后,我们list中就存放了所有的字符 "i like like like java do you like a java" //把list 中的数据放入到byte[] 并返回 byte[] bytes = new byte[list.size()]; for (int i = 0; i < list.size(); i++) { bytes[i] = list.get(i); } return bytes;
- 预处理传入的编码后的字节数组,将其转为一串二进制字符串
2.4 二叉排序树
2.4.1 一个需求
给你一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加。
- 解决方案
- 使用数组
数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢.
数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位置后,后面的数据需整体移动,速度慢。- 使用链式存储-链表
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动。
- 使用二叉排序树
- 二叉排序树介绍
二叉排序树:BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
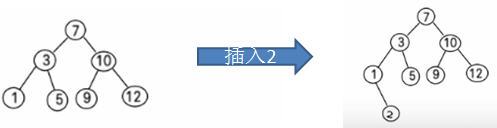
比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
2.4.2二叉排序树创建和遍历
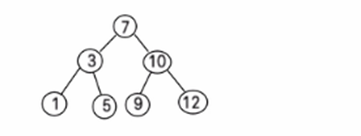
一个数组创建成对应的二叉排序树,并使用中序遍历二叉排序树,比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) , 创建成对应的二叉排序树为 :
2.4.3二叉排序树的删除
二叉排序树的删除情况比较复杂,有下面三种情况需要考虑:
- 删除叶子节点 (比如:2, 5, 9, 12)
- 删除只有一颗子树的节点 (比如:1)
- 删除有两颗子树的节点. (比如:7, 3,10 )

【思路分析】
删除一颗二叉树的思路,分为三种情况:
第一种情况:删除叶子节点(比如:2, 5, 9, 12)
思路分析:
(1)找到要删除的节点targetNode;
(2)找到要删除节点的父节点parentNode;
(3)判断要删除节点targetNode要删除节点targetNode是父节点parentNode的左子节点还是右子节点,
(3.1) 如果要删除节点targetNode是父节点parentNode的左子节点,parentNode.left=null,
(3.2) 如果要删除节点targetNode是父节点parentNode的右子节点,parentNode.right=null。
第二种情况:删除只有一颗子树的节点(比如:1)
思路分析:
(1)找到要删除的节点targetNode;
(2)找到要删除节点的父节点parentNode;
(3)确定targetNode有左子节点还是有右子节点;
(4)确定targetNode是parentNode的左子节点还是右子节点;
(5)如果targetNode有左子节点
(5.1) 如果targetNode是parentNode的左子节点,parentNode.left=targetNode.left;
(5.2)如果targetNode是parentNode的右子节点,parentNode.right=targetNode.left;
(6)如果targetNode有右子节点
(6.1) 如果targetNode是parentNode的左子节点,parentNode.left=targetNode.right;
(6.2)如果targetNode是parentNode的右子节点,parentNode.right=targetNode.right;
第三种情况:删除有两颗子树的节点(比如:7,3,10)
思路分析:
(1)找到要删除的节点targetNode;
(2)找到要删除节点的父节点parentNode;
(3)两种方法:
方法1:找到targetNode节点的右子节点的最小节点,使用临时变量temp将最小节点的值保存起来,
删除这个最小节点,并且将保存的temp赋值给targetNode,即:targetNode.val=temp;
方法2:找到targetNode节点的左子节点的最大节点,使用临时变量temp将最大节点的值保存起来,
删除这个最大节点,并且将保存的temp赋值给targetNode,即:targetNode.val=temp;
2.4.4代码实现
/**
* @author Wnlife
* @create 2019-12-10 20:08
* <p>
* 二叉排序树
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
for (int a : arr) {
binaryTree.add(new Node(a));
}
binaryTree.infixOrder();
// System.out.println("测试查找目标节点和目标节点的父节点~~");
// Node targetNode = binaryTree.searchTargetNode(2);
// Node parentNode = binaryTree.searchParentNode(targetNode);
// System.out.println("targetNode=" + targetNode);
// System.out.println("parentNode=" + parentNode);
System.out.println("删除节点测试~~");
binaryTree.deleteNode(3);
binaryTree.deleteNode(5);
binaryTree.deleteNode(7);
binaryTree.deleteNode(12);
binaryTree.deleteNode(10);
binaryTree.deleteNode(1);
binaryTree.deleteNode(2);
binaryTree.deleteNode(9);
binaryTree.infixOrder();
}
}
//二叉排序树
class BinaryTree {
private Node root;
//增加节点的方法
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
//前序遍历的方法
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("树为空~~");
}
}
/**
* 找到要删除的目标节点
*
* @param value 目标节点的值
* @return 要删除的targetNode节点,没有找到返回null
*/
public Node searchTargetNode(int value) {
if (root != null) {
return root.searchTargetNode(value);
} else {
System.out.println("~~排序二叉树为空~~");
return null;
}
}
/**
* 找到要删除节点的父节点
*
* @param node 要删除的节点
* @return 要删除节点的父节点, 没有找到返回null
*/
public Node searchParentNode(Node node) {
if (root != null) {
return root.searchParentNode(node);
} else {
System.out.println("~~排序二叉树为空~~");
return null;
}
}
/**
* 找到当前子树的最小节点的值
*
* @param node 当前子树的根节点
* @return 最小节点的值
*/
public int findSmallNode(Node node) {
while (node.left != null) {
node = node.left;
}
int temp = node.value;
deleteNode(temp);
return temp;
}
/**
* 删除一个节点
*
* @param value 要删除节点的值
*/
public void deleteNode(int value) {
//1.找到要删除的节点
Node targetNode = searchTargetNode(value);
if (targetNode == null) {
System.out.println("要删除的节点不存在!!!");
return;
}
//2.找到要删除节点的父节点
Node parentNode = searchParentNode(targetNode);
//第一种情况: 删除叶子节点
if (targetNode.left == null && targetNode.right == null) {
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {
parentNode.left = null;
} else {
parentNode.right = null;
}
} else {//如果父节点为空
root = null;
}
} else if (targetNode.left != null && targetNode.right != null) {//第三种情况:删除有两颗子树的节点
//方法1:找到targetNode节点的右子节点的最小节点,使用临时变量temp将最小节点的值保存起来,
//删除这个最小节点,并且将保存的temp赋值给targetNode,即:targetNode.val=temp;
int temp = findSmallNode(targetNode.right);
// System.out.println("smallNodeValue=" + smallNodeValue);
targetNode.value = temp;
} else {//第二种情况:删除只有一颗子树的节点
if (targetNode.left != null) {//如果targetNode有左子节点
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {//如果targetNode是parentNode的左子节点
parentNode.left = targetNode.left;
} else {//如果targetNode是parentNode的右子节点
parentNode.right = targetNode.left;
}
} else {//如果父节点为空
root = targetNode.left;
}
} else {//如果targetNode有右子节点
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {//如果targetNode是parentNode的左子节点
parentNode.left = targetNode.right;
} else {//如果targetNode是parentNode的右子节点
parentNode.left = targetNode.right;
}
} else {//如果父节点为空
root = targetNode.left;
}
}
}
}
}
//树节点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
//增加节点的方法
public void add(Node node) {
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
//前序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* 找到要删除的目标节点
*
* @param value 目标节点的值
* @return 要删除的targetNode节点,没有找到返回null
*/
public Node searchTargetNode(int value) {
if (this.value == value) {//找到,直接返回
return this;
}
if (value < this.value) {
if (this.left != null) {
return this.left.searchTargetNode(value);
}
} else {
if (this.right != null) {
return this.right.searchTargetNode(value);
}
}
return null;
}
/**
* 找到要删除节点的父节点
*
* @param node 要删除的节点
* @return 要删除节点的父节点, 没有找到返回null
*/
public Node searchParentNode(Node node) {
if ((this.left != null && this.left == node) || (this.right != null && this.right == node)) {
return this;
}
if (node.value < this.value) {
if (this.left != null) {
return this.left.searchParentNode(node);
}
} else {
if (this.right != null) {
return this.right.searchParentNode(node);
}
}
return null;
}
}
2.5 AVL树
2.5.1 看一个案例(说明二叉排序树可能的问题)
给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.

2.5.2 基本介绍
- 平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树, 可以保证查询效率较高。
- 具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
- 举例说明, 看看下面哪些AVL树, 为什么?
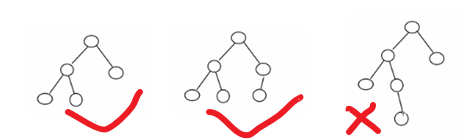
2.5.3 应用案例-单旋转(左旋转)
- 要求: 给你一个数列,创建出对应的平衡二叉树.数列 {4,3,6,5,7,8}
- 思路分析(示意图)

- 代码实现

2.5.4 应用案例-单旋转(右旋转)
- 要求: 给你一个数列,创建出对应的平衡二叉树.数列 {10,12, 8, 9, 7, 6}
- 思路分析(示意图)

- 代码实现

2.5.5 应用案例-双旋转
前面的两个数列,进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下,单旋转不能完成平衡二叉树的转换。比如数列:
int[] arr = { 10, 11, 7, 6, 8, 9 }; 运行原来的代码可以看到,并没有转成 AVL树.
int[] arr = {2,1,6,5,7,3}; // 运行原来的代码可以看到,并没有转成 AVL树
- 问题分析
经过右旋转后的树变为下图所示:

- 解决思路分析
2.1 问题分析出来: 在满足右旋转条件时,要判断
(1)如果是左子树的 右子树高度大于左子树的左子树高度时;
(2)就先对当前根节点的左子树进行左旋转,
(3)然后, 再对当前根节点进行右旋转即可;
否则,直接对当前节点(根节点)进行右旋转.即可。
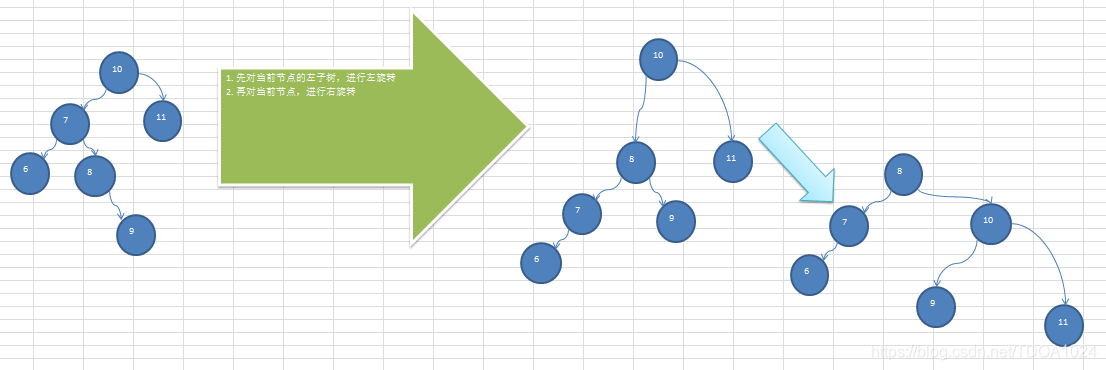
2.2 问题分析出来: 在满足左旋转条件时,要判断
(1)如果当前节点的右子树的左子树的高度大于当前节点右子树的右子树的高度;
(2)就对当前节点的右子树先进行右旋;
(3)然后再对当前节点进行左旋操作。
否则,直接对当前节点(根节点)进行左旋转.即可。
规律:
左旋操作必须是比较长的子树在右边
右旋操作必须是比较长的子树在坐边
不然就必须进行双旋操作
- 代码实现:
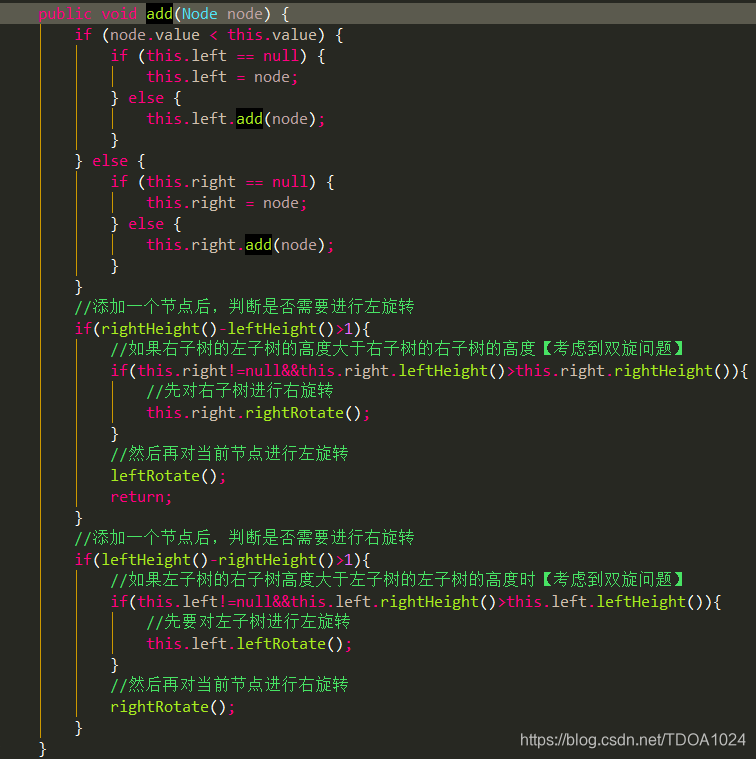
2.5.6 AVL树全部代码
/**
* @author Wnlife
* @create 2019-12-29 11:08
*
* AVL树:平衡二叉搜索树
*/
public class AVLTreeDemo {
public static void main(String[] args) {
AVLTree avlTree=new AVLTree();
// int []arr={4,3,6,5,7,8};
// int []arr={10,12, 8, 9, 7, 6};
int []arr={10, 11, 7, 6, 8, 9};
for (int i = 0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
System.out.println("中序遍历");
avlTree.infixOrder();
//树高4,左子树高1,右子树高3
System.out.println("树的高度="+avlTree.getRoot().height());
System.out.println("树的左子树的高度="+avlTree.getRoot().leftHeight());
System.out.println("树的右子树的高度="+avlTree.getRoot().rightHeight());
}
}
/**
* AVLTree
*/
class AVLTree{
private Node root;
public Node getRoot() {
return root;
}
/**
* 增加节点的方法
* @param node
*/
public void add(Node node) {
if (root == null) {
root = node;
} else {
root.add(node);
}
}
/**
* 前序遍历的方法
*/
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("树为空~~");
}
}
/**
* 找到要删除的目标节点
*
* @param value 目标节点的值
* @return 要删除的targetNode节点,没有找到返回null
*/
public Node searchTargetNode(int value) {
if (root != null) {
return root.searchTargetNode(value);
} else {
System.out.println("~~排序二叉树为空~~");
return null;
}
}
/**
* 找到要删除节点的父节点
*
* @param node 要删除的节点
* @return 要删除节点的父节点, 没有找到返回null
*/
public Node searchParentNode(Node node) {
if (root != null) {
return root.searchParentNode(node);
} else {
System.out.println("~~排序二叉树为空~~");
return null;
}
}
/**
* 找到当前子树的最小节点的值
*
* @param node 当前子树的根节点
* @return 最小节点的值
*/
public int findSmallNode(Node node) {
while (node.left != null) {
node = node.left;
}
int temp = node.value;
deleteNode(temp);
return temp;
}
/**
* 删除一个节点
*
* @param value 要删除节点的值
*/
public void deleteNode(int value) {
//1.找到要删除的节点
Node targetNode = searchTargetNode(value);
if (targetNode == null) {
System.out.println("要删除的节点不存在!!!");
return;
}
//2.找到要删除节点的父节点
Node parentNode = searchParentNode(targetNode);
//第一种情况: 删除叶子节点
if (targetNode.left == null && targetNode.right == null) {
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {
parentNode.left = null;
} else {
parentNode.right = null;
}
} else {//如果父节点为空
root = null;
}
} else if (targetNode.left != null && targetNode.right != null) {//第三种情况:删除有两颗子树的节点
//方法1:找到targetNode节点的右子节点的最小节点,使用临时变量temp将最小节点的值保存起来,
//删除这个最小节点,并且将保存的temp赋值给targetNode,即:targetNode.val=temp;
int temp = findSmallNode(targetNode.right);
// System.out.println("smallNodeValue=" + smallNodeValue);
targetNode.value = temp;
} else {//第二种情况:删除只有一颗子树的节点
if (targetNode.left != null) {//如果targetNode有左子节点
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {//如果targetNode是parentNode的左子节点
parentNode.left = targetNode.left;
} else {//如果targetNode是parentNode的右子节点
parentNode.right = targetNode.left;
}
} else {//如果父节点为空
root = targetNode.left;
}
} else {//如果targetNode有右子节点
if (parentNode != null) {//如果父节点不为空
if (parentNode.left == targetNode) {//如果targetNode是parentNode的左子节点
parentNode.left = targetNode.right;
} else {//如果targetNode是parentNode的右子节点
parentNode.left = targetNode.right;
}
} else {//如果父节点为空
root = targetNode.left;
}
}
}
}
}
/**
* 树节点
*/
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
/**
* 返回当前节点的左子树的高度
* @return
*/
public int leftHeight() {
if(this.left==null){
return 0;
}else {
return this.left.height();
}
}
/**
* 返回当前节点的右子树的高度
* @return
*/
public int rightHeight(){
if(this.right==null){
return 0;
}else {
return this.right.height();
}
}
/**
* 返回以该节点为根节点的树的高度
* @return 树的高度
*/
public int height(){
return Math.max(this.left == null ? 0 : this.left.height(),
this.right == null ? 0 : this.right.height()) + 1;
}
/**
* 左旋转:降低右子树的高度
*/
public void leftRotate(){
//1.创建一个新的节点newNode(以4这个值创建),值等于当前根节点的值
Node newNode = new Node(this.value);
//2.把新节点的左子树设置为当前节点的左子树
newNode.left = this.left;
//3.把新节点的右子树设置为当前节点的右子树的左子树
newNode.right = this.right.left;
//4.把当前节点的值换为右子节点的值
this.value = this.right.value;
//5.把当前节点的右子树设置为右子树的右子树
this.right = this.right.right;
//6.把当前节点的左子树设置为新节点
this.left = newNode;
}
/**
* 右旋转:降低左子树的高度
*/
public void rightRotate(){
//1.创建一个新的节点,值等于当前根节点的值
Node newNode = new Node(this.value);
//2.把新节点的右子树设置为当前节点的右子树
newNode.right = this.right;
//3.把新节点的左子树设置为当前节点的左子树的右子树
newNode.left = this.left.right;
//4.把当前节点的值替换为左子节点的值
this.value = this.left.value;
//5.把当前节点的左子树设置为左子树的左子树
this.left = this.left.left;
//6.把当前节点的右子树设置为新节点
this.right = newNode;
}
/**
* 增加节点的方法
* @param node
*/
public void add(Node node) {
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
//添加一个节点后,判断是否需要进行左旋转
if(rightHeight()-leftHeight()>1){
//如果右子树的左子树的高度大于右子树的右子树的高度【考虑到双旋问题】
if(this.right!=null&&this.right.leftHeight()>this.right.rightHeight()){
//先对右子树进行右旋转
this.right.rightRotate();
}
//然后再对当前节点进行左旋转
leftRotate();
return;
}
//添加一个节点后,判断是否需要进行右旋转
if(leftHeight()-rightHeight()>1){
//如果左子树的右子树高度大于左子树的左子树的高度时【考虑到双旋问题】
if(this.left!=null&&this.left.rightHeight()>this.left.leftHeight()){
//先要对左子树进行左旋转
this.left.leftRotate();
}
//然后再对当前节点进行右旋转
rightRotate();
}
}
/**
* 前序遍历
*/
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* 找到要删除的目标节点
*
* @param value 目标节点的值
* @return 要删除的targetNode节点,没有找到返回null
*/
public Node searchTargetNode(int value) {
//找到,直接返回
if (this.value == value) {
return this;
}
if (value < this.value) {
if (this.left != null) {
return this.left.searchTargetNode(value);
}
} else {
if (this.right != null) {
return this.right.searchTargetNode(value);
}
}
return null;
}
/**
* 找到要删除节点的父节点
*
* @param node 要删除的节点
* @return 要删除节点的父节点, 没有找到返回null
*/
public Node searchParentNode(Node node) {
if ((this.left != null && this.left == node) || (this.right != null && this.right == node)) {
return this;
}
if (node.value < this.value) {
if (this.left != null) {
return this.left.searchParentNode(node);
}
} else {
if (this.right != null) {
return this.right.searchParentNode(node);
}
}
return null;
}
}
2.6 多路查找树
2.6.1 二叉树与B树
- 二叉树的问题分析
二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树:
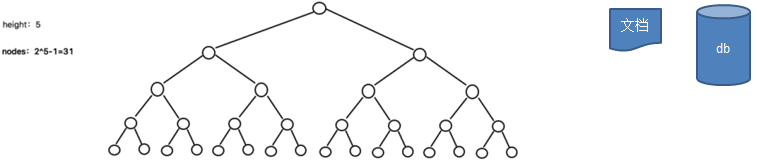
- 二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如1亿), 就存在如下问题:
- 问题1:在构建二叉树时,需要多次进行i/o操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响;
- 问题2:节点海量,也会造成二叉树的高度很大,会降低操作速度。
- 多叉树
- 在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree)。
- 后面我们讲解的2-3树,2-3-4树就是多叉树,多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
- 举例说明(下面2-3树就是一颗多叉树)
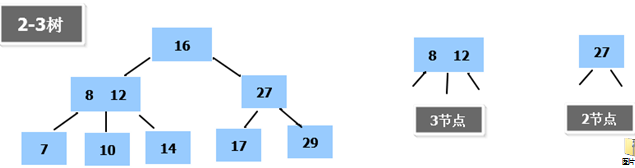
- B树的基本介绍
B树通过重新组织节点,降低树的高度,并且减少i/o读写次数来提升效率。

- 如图B树通过重新组织节点, 降低了树的高度.
- 文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个页(页得大小通常为4k),这样每个节点只需要一次I/O就可以完全载入。
- 将树的度M设置为1024,在600亿个元素中最多只需要4次I/O操作就可以读取到想要的元素, B树(B+)广泛应用于文件存储系统以及数据库系统中
- Note:节点的度指的是一个节点的子节点的个数,数的度指的是一个树中所有节点的最大的度数。
2.6.2 2-3树
- 2-3树基本介绍
- 2-3树是最简单的B树结构, 具有如下特点:
- 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点. - 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点.
- 2-3树是由二节点和三节点构成的树。
- 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件)
- 2-3树应用案例
将数列{16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成2-3树,并保证数据插入的大小顺序。
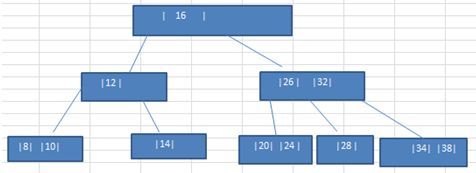
插入规则:
- 2-3树的所有叶子节点都在同一层.(只要是B树都满足这个条件);
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点;
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点;
- 当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足上面3个条件。
- 对于三节点的子树的值大小仍然遵守(BST 二叉排序树)的规则。
- 其他说明
除了23树,还有234树等,概念和23树类似,也是一种B树。 如图:
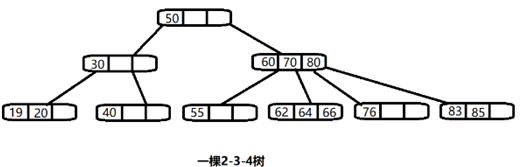
2.6.3 B树、B+树和B*树
- B树的介绍
B-tree树即B树,B即Balanced,平衡的意思。有人把B-tree翻译成B-树,容易让人产生误解。会以为B-树是一种树,而B树又是另一种树。实际上,B-tree就是指的B树。
前面已经介绍了2-3树和2-3-4树,他们就是B树(英语:B-tree 也写成B-树),这里我们再做一个说明,我们在学习Mysql时,经常听到说某种类型的索引是基于B树或者B+树的,如图:

B树的说明:
- B树的阶:节点的最多子节点个数。比如2-3树的阶是3,2-3-4树的阶是4;
- B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点;
- 关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找。
- B+树的介绍
B+树是B树的变体,也是一种多路搜索树。
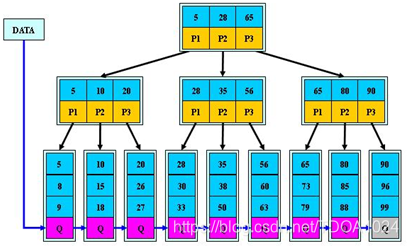
2.B+树的说明:
- B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
- 所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)恰好是有序的;
- 不可能在非叶子结点命中;
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
- 更适合文件索引系统;
- B树和B+树各有自己的应用场景,不能说B+树完全比B树好,反之亦然.。
- B树的介绍
B树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针。
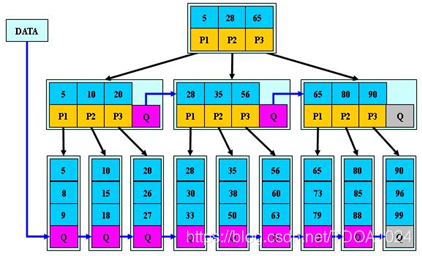
- B*树的说明:
- B*树定义了非叶子结点关键字个数至少为(2/3)*M,(M表示树的度)即块的最低使用率为2/3,而B+树的块的最低使用率为1/2;
- 从第1个特点我们可以看出,B*树分配新结点的概率比B+树要低,空间使用率更高。





















 5006
5006











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








