

Exercise 3.1-1
设max ( f(n) , g(n) ) = g(n),又由max ( f(n) , g(n) ) = Θ(f(n) + g(n)) ,
即证 c1* ( f(n) + g(n) ) ≤ g(n) ≤ c2* ( f(n) +g(n) ), 取c1=1/2 ,c2=1 即可。
参考答案:由于我们要求f和g都是渐近非负的,假设我们超过了某个n1,其中它们都是非负的(取f和g对应的n的两个边界的最大值)。设c1 = 0.5和c2 = 1。
0 ≤ 0 . 5( f ( n ) + g ( n )) ≤ 0 . 5(max( f ( n ) , g ( n )) + max( f ( n ) , g ( n )))= max( f ( n ) , g ( n )) ≤ max( f ( n ) , g ( n )) + min( f ( n ) , g ( n )) = ( f ( n ) + g ( n ))
Exercise 3.1-2
即证 c1* n^b ≤ (n+a) ^ b ≤ c2* n^b ,取c1 = 1 , c2 = (1+a)^b 即可。
1.(证明上界)设c = 2^b , n0 ≥ 2*a。那么对于所有n ≥ n0 ,我们有(n + a)^b ≤ (2*n)^b = c * n^b(我们有
),因此 (n+a)^b = O(n^b)(因此
) 。
2.(证明下界)设 n0 ≥ − a / (1- 1/2^(1/b)) ,c = 1/2 (
),
那么
当且仅当
当且仅当
当且仅当
,因此
。
根据定理3.1,
因此,(n+a)^b = Θ(n^b)。(
)
至少意指下界,O意指上界。
有很多不同的函数的增长率小于或等于n2。特别是常数函数或收缩到0的速度可以任意快。说增长速度比收缩到零的函数快,没有任何意义。
Exercise 3.1-4
对于所有n≥0,2^(n+1)≥2·2^n,所以2^(n+1) = O(2^n)。然而,2^(2n)不等于O(2^n)。如果是,那么就会存在n0和c,使得n≥n0意味着(2^n)·(2^n) = 2^(2*n)≤c*(2^n),所以当n≥n0时,2^n≤c,这显然是不可能的,因为c是常数。
Exercise 3.1-5
假设f(n)∈Θ(g(n)),则∃c1, c2, n0,∀n≥n0,0≤c1g(n)≤f(n)≤c2g(n),如果我们单独看这些不等式,我们有c1g(n)≤f(n) (f(n)∈Ω(g(n))和f(n)≤c2g(n) (f(n)∈O(g(n)))。
假设我们有∃n1, c1,∀n≥n1, c1g(n)≤f(n)和∃n2, c2,∀n≥n2, f(n)≤c2g(n)。把这些放在一起,并让n0 = max(n1, n2),我们有∀n≥n0, c1g(n)≤f(n)≤c2g(n)。
Exercise 3.1-6
假设运行时间为Θ(g(n))。根据3.1定理,运行时间为O(g(n)),这意味着对于任何大小为n≥n0的输入,对于某个c1,运行时间上界为c1g(n)。这包括最坏情况下输入的运行时间。定理3.1还暗示运行时间为Ω(g(n)),这意味着对于任何大小为n≥n0的输入,对于某些c2,运行时间以c2g(n)为界。这包括最佳情况输入的运行时间。另一方面,任何输入的运行时间都以最坏情况的运行时间为界,以最佳情况的运行时间为界。如果最坏情况和最佳情况的运行时间分别是O(g(n))和Ω(g(n)),那么任何大小为n的输入的运行时间必须是O(g(n))和Ω(g(n))。定理3.1推导出运行时间为Θ(g(n))。
Exercise 3.1-7
集合证明: o( g(n) ) 即 0 ≤ f(n) < c* g(n) ; ω( g(n) ) 即 0 ≤ c* g(n) <f(n) 。
极限的矛盾:假设我们有f(n)∈o(g(n))∩ω(g(n))。然后,我们有一个矛盾
。
Exercise 3.1-8
Ω(g(n, m)) = {f(n, m):存在正常数c, n0和m0,使得对于所有n≥n0或m≥m0,f(n, m)≥cg(n, m) }
Θ(g(n, m)) = {f(n, m):存在正常数c1, c2, n0和m0,使得对于所有n≥n0或m≥m0,c1g(n,m)≤f(n, m≤c2g(n, m)}
Exercise 3.2-1

设n1 < n2为任意值。
1)由于f和g是单调递增的,我们知道f(n1) < f(n2),g(n1) < g(n2)。所以f(n1) + g(n1) < f(n2) + g(n2)。
2)由于g (n1) < g (n2),我们有f (g (n1)) < f (g (n2))。
最后,如果两者都是非负的,则
f(n1)g(n1) = f(n2)g(n1) + (f(n2) - f(n1))g(n1)
= f(n2)g(n2) + f(n2)(g(n2) - g(n1)) + (f(n2) - f(n1))g(n1)
3)由于f(n1)≥0,f(n2) > 0,因此,式中的第二项大于零。第三项是非负的,所以整个<f(n2)g(n2)
Exercise 3.2-2

Exercise 3.2-3
![]()
正如提示所示,我们将应用斯特林近似
注意最后一项是O(lg(n))。如果我们把分解lg得到的两个表达式相加而不是相减。整个表达式由nlg (n)支配。我们得到lg(n!) = Θ(nlg (n))。
如果我们限制n > 4e,那么这是
Exercise 3.2-4
![]()
函数不是多项式有界的。如果有,则存在常数c, a,和n0,使得对于所有n≥n0,不等式
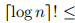
成立。特别地,当n = 2 ^ k时成立。对于k∈n,则这变成了
,这是一个矛盾,因为阶乘函数不是指数有界的。
我们会证明,在不失一般性的前提下,假设
,那么这就等价于证明
,或
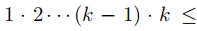
,对于k≥1,这显然是正确的。因此它是多项式有界的。
注意lg∗(2n) = 1 + lg∗(n),因此,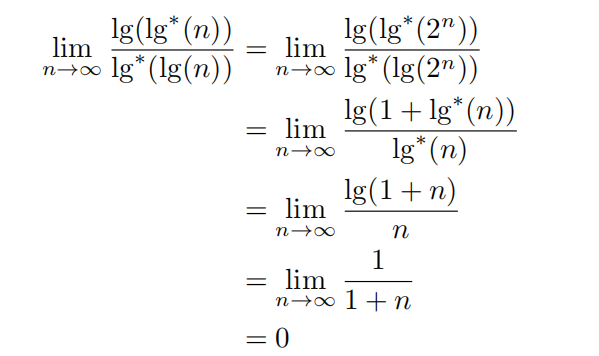
我们得出 lg * (lg(n))增长得更快
Exercise 3.2-7

首先,证明
。因此,对于每一个i,
,
同理。
当i = 0,
当i = 1,
然后,通过归纳法,
Exercise 3.2-8
设c1和c2满足c1*n ≤ klnk ≤ c2*n。然后我们有ln c1 + ln n =ln(c1n) ≤ ln(k ln k) = ln k + ln(ln k)所以ln n = O(ln k)。令c3满足ln n≤c3 ln k,那么
因此,n / ln n = Ω(k)。类似地,我们有ln k + ln(ln k) =ln(k ln k) ≤ ln(c2 n) = ln(c2) + ln(n)所以ln(n) = Ω(ln k)。令c4满足ln n≥c4 ln k,那么
使n / ln n = O(k)。由3.1定理可知 n / ln n = Θ(k)。根据对称性,k = Θ(n / ln n)。









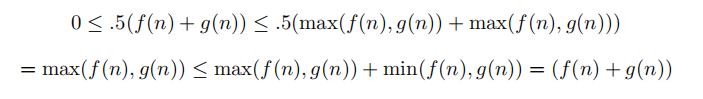


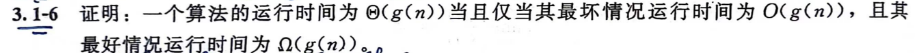

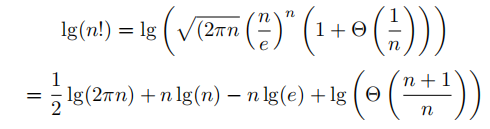
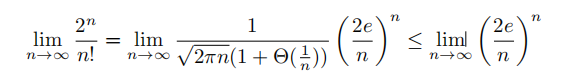

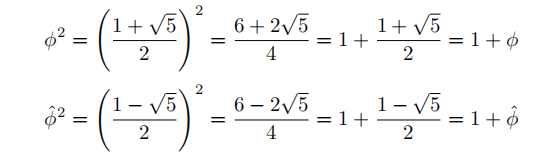
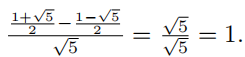
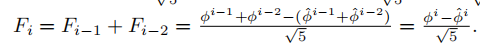

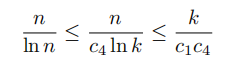














 1961
1961











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








