动态规划法

目录

内容

我的分析

问题解决

总结（列举一些常见问题并回答）

---

内容

1.斐波那契数列 

（1）自底向上

（2）自顶向下 

2.走棋盘

3.爬台阶问题 

4.挖金矿问题

我的分析

1.斐波那契数列：

目的：求第n个斐波那契数；

思路：采用动态规划的方法，有两种思路，自底向上和自顶向下。若采用自顶向下的方法，因为采用递归会导致重复子问题的计算，所以用数组保存已经求解过的值，首先先把数组初始化每个值为-1，若第n个数组的值为-1说明这个数还没有计算，则先计算再保存，其他思路和递归相同。若采用自底向上的思路，则直接循环执行b[i]=b[i-1]+b[i-2]即可。

2.走棋盘问题：

目的：求解从起点到终点所有的路径条数。

思路：求解（n，m）的路径数=（n-1，m）的路径数+（n，m-1）的路径数，和斐波那契类似需要把已经算过的值保存下来。

3.爬台阶问题：

目的：每次可以爬1阶或2阶台阶，求爬到第n阶台阶有几种方法。

思路：此类问题都很类似，求第n阶的方法即为第n-1阶和n-2阶方法的和，总体思路和斐波那契很像。

4.挖金矿问题：

目的：有n个工人，m座金矿，每个金矿需要n1个人挖，价值为w，每个金矿要嘛挖，要嘛不挖，求最大的价值。

思路：每一层的求解结果都可以由下层（底层）推导得到，因此可以使用一个表来记录所有已解决的子问题的答案，即而得到最优解

问题解决

1、斐波那契数列：

算法描述：

算法：自顶向下求斐波那契getFibtop（）

输入：第n个数的下标，保存数据的数组a[]

输出：第n个斐波那契的值。

过程： 1、初始化数组a[]中的值为-1；

2、判断数组a[]中是否有录入 数据

               2.1如果有返回a[]

           3、将第一项和第二项赋值为1

  4、a[n]=getFibtop(n-1,a)+getFibtop(n-2,a);

5、返回a[n]

算法实现：

运行结果：

时间复杂度：O（n）

算法描述：

算法：自底向上求解斐波那契数列getFibdowm（）

输入：要求的第n个数下标

输出：第n个数的值

过程：1、定义数组b并初始化b[1]=1;b[2]=1;

          2、定义循环变量i，循环变量i从2到n执行以下：

      2.1b[i]=b[i-1]+b[i-2]

3、返回b[n]

算法实现：

运行结果：

时间复杂度：O(n)

2、走棋盘问题：

算法描述：

算法：从起点到终点的路径条数getPath（）

输入：二维数组[][]s；终点的横坐标m，纵坐标n

输出：路径条数s[m][n]

过程：1、将起始点所在行赋值为1

           2、将起始点所在列赋值为1

          3、遍历行和列执行以下：

      3.1、s[i][j]=s[i-1][j]+s[i][j-1]

4、返回s[m][n]

            算法实现：

            

运行结果：

时间复杂度：

T(n)=m+n+(m-1)*(n-1)=m*m+1->O(n)=n*m

      3、爬台阶问题：

       算法描述：

    算法：求爬台阶的方法climbStairs（）（一次可以爬一阶或两阶）

   输入：数组[]d,爬的台阶数n

   输出：爬台阶的方法d[n]

  过程：1、初始化d[1]=1 d[2]=2

             2、定义循环变量i，i从3到n执行以下：

2.1、int sum = d[1]+d[2];
 2.2、  d[1]=d[2];
 2.3、  d[2]=sum;

3、返回d[2]
 

算法实现：

运行结果：

时间复杂度：

T(n)=3*(n-2)+2=3n-4 ->O(n)=n

4、挖金矿问题：

算法描述：

算法：求挖金矿的最大价值getBestGoldMining（）

输入：工人数量为w，金矿的含金量为数组g[]，金矿所需开采人数设为数组p[]

输出：金矿的最大价值

过程：1、创建表格

           2、填充表格

           3、返回最后一个格子的值

算法实现：

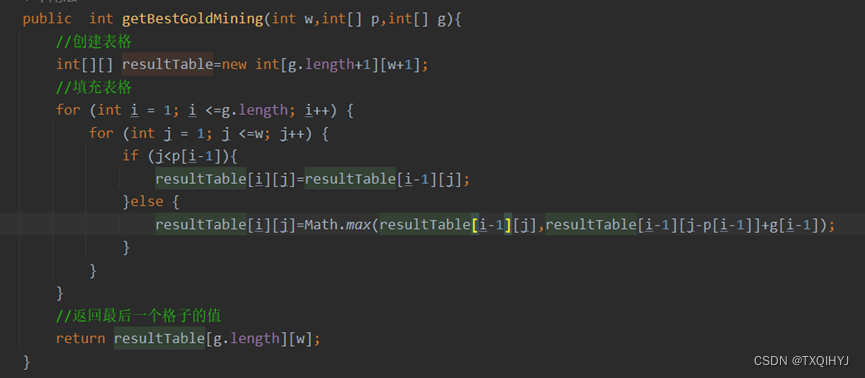
运行结果：

时间复杂度：

T（n）= n*m  ->O(n)=n*m

总结（列举一些常见问题并回答）

1.如果用分治函数实现斐波那契数列,该函数被调用几次? 而用自顶向下递归备忘实现时，该函数又被调用几次？ 自底向上迭代填表时，又被调用几次？请你给出1个n的具体值，画图回答以上问题。

2.请从你实现的级别中选择一题，说明动态规划法的解决过程（划分阶段、逆向

推导、正向计算），再针对实现说明是自底向上或是自顶向下。（例：级别为“中”，就从走棋盘或者找零钱中选择一道题来分析。）

    挖金矿问题：

    填表法：填充一人一个金矿，一人两个金矿，两个一个金矿…n人m个金矿获得的最大值，最后即为所求。

    自底向上实现。

3.你觉得动态规划法和分治法有区别吗？请举例说明。

动态规划减少了重复子问题的计算，比如斐波那契数列的计算，使用分治法会重复计算子问题如：求F（5）的话F（2）会计算3便而动态规划法每种子问题只会计算一遍。

4.动态规划法的两种实现有区别吗？你觉得动态规划法能解决所有问题吗？

自底向上的分析是从具体到抽象，自顶向下是从抽象到具体。

不能解决所有问题，不存在动态规划要求的重叠子问题如N皇后问题就无法用动态规划解决。