〇、写在前面
最就在九月一日,百度来到了哈尔滨工业大学进行2020年校招,我有幸去参观了一下宣讲会,感慨良多,作为入门paddlepaddle的契机,我决定开启这个专栏——PaddlePaddle炼丹,学习一下国产深度学习框架,paddlepaddle。关于paddlepaddle的详情,欢迎查看这个博客——PaddlePaddle百度深度学习框架:等待你我一起划桨的AI大船。
一、百度简介

百度(纳斯达克:BIDU),全球最大的中文搜索引擎及最大的中文网站,全球领先的人工智能公司,据说是中国第一,世界第二。“百度”二字,来自于八百年前南宋词人辛弃疾的一句词:众里寻他千百度,这句话描述了词人对理想的执着追求。
讲道理,不管BAT的问题,我很喜欢,什么是BAT?
BAT,B指百度、A指阿里巴巴、T指腾讯,是中国互联网公司百度公司(Baidu)、阿里巴巴集团(Alibaba)、腾讯公司(Tencent)三大互联网公司首字母的缩写。其中百度总部在北京、阿里巴巴总部在浙江省杭州市、腾讯总部在广东省深圳市。
二、百度飞桨
飞桨(PaddlePaddle)是国内唯一功能完备的端到端开源深度学习平台,致力于让深度学习技术的创新与应用更简单。
关于paddlepaddle的详情,欢迎查看这个博客——PaddlePaddle百度深度学习框架:等待你我一起划桨的AI大船
No 废话,直接 Action!!!
三、快速安装
- PaddlePaddle支持使用pip快速安装, 执行下面的命令完成CPU版本的快速安装:
pip install -U paddlepaddle
- 如需安装GPU版本的PaddlePaddle,执行下面的命令完成GPU版本的快速安装:
pip install -U paddlepaddle-gpu
手头的电脑还是 Windows 10 的系统,就直接使用pip进行安装了。
关于pip的详细信息,欢迎查看这个博客——python中pip安装、升级、升级指定的包

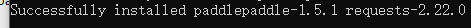
successfully 了,也就是安装成功了,新版本的 paddlepaddle 是基于 fluid 的。
四、快速使用
首先,需要导入 fluid 库
import paddle.fluid as fluid
Tensor操作
下面几个简单的案例,来了解一下 Fluid:
- 使用Fluid创建5个元素的一维数组,其中每个元素都为1
# 定义数组维度及数据类型,可以修改shape参数定义任意大小的数组
data = fluid.layers.ones(shape=[5], dtype='int64')
# 在CPU上执行运算
place = fluid.CPUPlace()
# 创建执行器
exe = fluid.Executor(place)
# 执行计算
ones_result = exe.run(fluid.default_main_program(),
# 获取数据data
fetch_list=[data],
return_numpy=True)
# 输出结果
print(ones_result[0])

- 使用Fluid将两个数组按位相加
# 调用 elementwise_op 将生成的一维数组按位相加
add = fluid.layers.elementwise_add(data,data)
# 定义运算场所
place = fluid.CPUPlace()
exe = fluid.Executor(place)
# 执行计算
add_result = exe.run(fluid.default_main_program(),
fetch_list=[add],
return_numpy=True)
# 输出结果
print (add_result[0])

- 使用Fluid转换数据类型
# 将一维整型数组,转换成float64类型
cast = fluid.layers.cast(x=data, dtype='float64')
# 定义运算场所执行计算
place = fluid.CPUPlace()
exe = fluid.Executor(place)
cast_result = exe.run(fluid.default_main_program(),
fetch_list=[cast],
return_numpy=True)
# 输出结果
print(cast_result[0])
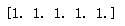
五、线性回归模型
这是一个简单的线性回归模型,可以快速求解四元一次方程。
1)基于paddlepaddle的代码:
#加载库
import paddle.fluid as fluid
import numpy as np
import time
start = time.clock()
#生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(10, 4))
res = []
for i in range(10):
# 假设方程式为 y=4a+6b+7c+2d
y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
res.append([y])
# 定义数据
train_data=np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')
#定义网络
x = fluid.layers.data(name="x",shape=[4],dtype='float32')
y = fluid.layers.data(name="y",shape=[1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)
#定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)
#定义优化方法
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)
#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())
##开始训练,迭代500次
for i in range(500):
outs = exe.run(
feed={'x':train_data,'y':y_true},
fetch_list=[y_predict.name,avg_cost.name])
if i%50==0:
print ('iter={:.0f},cost={}'.format(i,outs[1][0]))
#存储训练结果
params_dirname = "result"
fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)
elapsed = (time.clock() - start)
print("Training Time used:",elapsed)
# 开始预测
infer_exe = fluid.Executor(cpu)
inference_scope = fluid.Scope()
# 加载训练好的模型
with fluid.scope_guard(inference_scope):
[inference_program, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)
# 生成测试数据
test = np.array([[[9],[5],[2],[10]]]).astype('float32')
# 进行预测
results = infer_exe.run(inference_program,
feed={"x": test},
fetch_list=fetch_targets)
# 给出题目为 【9,5,2,10】 输出y=4*9+6*5+7*2+10*2的值
print ("9a+5b+2c+10d={}".format(results[0][0]))
elapsed2 = (time.clock() - start)
print("Testing Time used:",elapsed2)
运行结果如下,花费时间为3.445s。
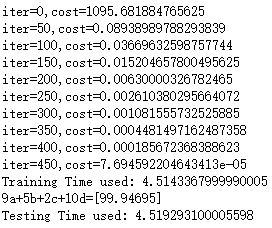
输出结果应是一个近似等于100的值,每次计算结果略有不同。
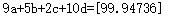
让我们把 paddlepaddle 与 TensorFlow 进行对比,可以发现两者的不同。
2)基于TensorFlow的代码:
# 训练代码
import tensorflow as tf
import numpy as np
import time
start = time.clock()
# 生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(10, 4))
res = []
for i in range(10):
# 假设方程式为 y=4a+6b+7c+2d
y = 4 * outputs[i][0] + 6 * outputs[i][1] + \
7 * outputs[i][2] + 2 * outputs[i][3]
res.append([y])
# 定义数据
train_data = np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')
# 占位符
x = tf.placeholder(tf.float32, shape=[None, 4], name='x')
y = tf.placeholder(tf.float32, shape=[None, 1], name='y')
# w 是要求的各个参数的权重,是目标输出,对应 t_w
w = tf.Variable(np.ones(4, dtype=np.float32).reshape((4, 1)), tf.float32)
# 实际输出数据
y_ = tf.matmul(x, w)
# 定义损失函数,均方误差
loss = tf.reduce_mean(tf.square(y - y_))
# 定义一个梯度下降算法来进行训练的优化器
optimizer = tf.train.GradientDescentOptimizer(0.05)
# 最小化代价函数
train = optimizer.minimize(loss)
# 初始化变量
init = tf.global_variables_initializer()
# 开始训练
with tf.Session() as sess:
sess.run(init)
for step in range(500):
_, curr_loss = sess.run([train,loss], feed_dict={x: train_data, y: y_true})
if step % 50 == 0:
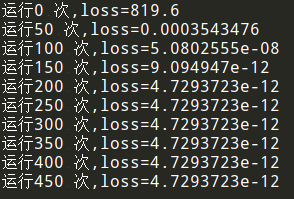
print("运行%d 次,loss=%s" % (step,curr_loss))
#用saver 保存模型
saver = tf.train.Saver()
saver.save(sess, "model_data/model")
elapsed = (time.clock() - start)
print("Training Time used:",elapsed)

# 测试代码
import tensorflow as tf
import numpy as np
def main():
sess = tf.InteractiveSession()
# 加载模型
saver = tf.train.import_meta_graph('model_data/model.meta')
saver.restore(sess, 'model_data/model')
graph = tf.get_default_graph()
# 得到当前图中所有变量的名称
# tensor_name_list = [tensor.name for tensor in graph.as_graph_def().node]
# print(tensor_name_list)
x = graph.get_tensor_by_name('x:0')
pre_result = graph.get_tensor_by_name("MatMul:0")
# 生成测试数据
test = np.array([[9,5,2,10]]).astype('float32')
# 进行预测
pre_reload_out = sess.run(pre_result, feed_dict={x: test})
print("9a+5b+2c+10d={}".format(pre_reload_out))
# 关闭会话
sess.close()
if __name__ == '__main__':
main()
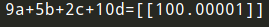

经过非严谨地对比,我们可以发现TensorFlow的代码量明显要多很多,无论是训练还是测试,但是paddlepaddle就相当的简约了,这也是paddlepaddle的一个大优势,但是TensorFlow的训练时间要更短一些,当然我的测试可能存在偶然性。。。
六、总结
总体来说,paddlepaddle给我的感觉体验确实要更好一些,对一些新入门的童鞋更友好,friendly,更容易上手一些,接下来会学习一下paddlepaddle的相关知识,写一写学习笔记,期待一下!!!😃
如果想要更多的资源,欢迎关注 @我是管小亮,文字强迫症MAX~
回复【福利】即可获取我为你准备的大礼,包括C++,编程四大件,NLP,深度学习等等的资料。
想看更多文(段)章(子),欢迎关注微信公众号「程序员管小亮」~

























 1067
1067

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










