【内功修炼】二叉树的那些事

最近上数据结构的课讲到了二叉树，课上听得云里雾里的，妈蛋，还不如老子自学呢！尽管具体算法都基本搞懂，但知识需要总结才能串起来。
目录：

二叉树的创建与删除

给出创建算法之前先给出二叉树类和二叉树结点结构体的定义吧(^__^)

//定义结点结构体
template <class T>
struct BintreeNode
{
    T data;
    BintreeNode<T>* pLeftTree;
    BintreeNode<T>* pRightTree;
    BintreeNode<T>* parent;
    BintreeNode() :pLeftTree(NULL), pRightTree(NULL){}
    BintreeNode(T x, BintreeNode<T>* pLeftTree=NULL,BintreeNode<T>* pRightTree = NULL) :data(x),pLeftTree(pLeftTree), pRightTree(pRightTree){}
};
//定义二叉树类
template <class T>
class Bintree{
public:
    Bintree() :pRoot(NULL){};
    ~Bintree(){ _destroyTree(pRoot); }
    BintreeNode<T>* createBintree();
    BintreeNode<T>* createBintree(T * VLR, T* LVR, int n);
    void preOrder(BintreeNode<T>* root);
    void inOrder(BintreeNode<T>* root);
    void postOrder(BintreeNode<T>* root);
    void levelOrder(BintreeNode<T>* root);
    void preOrder();
    void inOrder();
    void postOrder();
    void levelOrder();
private:
    BintreeNode<T>* pRoot;
    void _destroyTree(BintreeNode<T>* p);
    void visit(BintreeNode<T>* p);
};

类似于广义表的创建算法

就是要求用户按格式输入字符串来创建二叉树，跟广义表的创建非常类似。
创建过程需要一个辅助栈以及辅助变量k用于标记是在创建左子树还是右子树。
1、输入data时，比如一个’A’, new一个结点(*p)，这时分两个情况。a、根节点pRoot为空，那么新节点(p)就是根节点了，pRoot指向新节点(p)；b、根节点pRoot不为空，那么如果k==-1(表示正在创建左子树）就让栈顶的节点的左指针指向新节点(P)，如果k==1（表示正在创建右子树）就让栈顶的节点的右子针指向新节点。
2、输入’(‘时，k=-1,标志开始创建左子树，将节点p压栈。
3、输入’,’时，k=1，标志开始创建右子树。
4、输入’)’时，表示该节点p的孩子已经安置好了(＾－＾)V，出栈，pop();
好，上代码<(￣︶￣)>

template <class T>
BintreeNode<T>* Bintree<T>::createBintree(){
    if (pRoot != NULL){
        cout << "该二叉树实例是非空树，无法创建" << endl;
        return pRoot;
    }
    char RefValue = '#';//结束创建的标志
    stack<BintreeNode<T>*> s;
    BintreeNode<T>*p, *r;//p用来指向new出来的节点，r用来取出栈顶的节点
    int k;//辅助变量k用于标记是在创建左子树还是右子树。
    char in;
    cin >> in;
    while (in != RefValue){
        switch (in)
        {
        case '(': k = -1; s.push(p);//表明p指向的树节点有儿子，调整k的值进入左子树，p入栈
            break;
        case ')': s.pop();
            break;
        case ',':k = 1;
            break;
        default: p = new BintreeNode<T>(in);
            if (pRoot == NULL){
                pRoot = p;
            }
            else if (k == -1){
                r = s.top();
                r->pLeftTree = p;
            }
            else{
                r = s.top();
                r->pRightTree = p;
            }
            break;
        }
        cin >> in;
    }
    return pRoot;
    }

利用前序和中序遍历的递归创建算法

这个算法很优美，因为用到了递归( ^_^ )。理论基础是前序和中序遍历一起唯一确定一棵二叉树。
下面直接上代码

template<class T>
BintreeNode<T>* Bintree<T>::createBintree(T* VLR, T* LVR, int n)
{//VLR和LVR分别表示存储前序和中序的数组，传过来的是数组的指针其实可以理解成数组的首地址，n表示当前结点数
    if (n == 0)
        return NULL;
    int k = 0;
    while (VLR[0] != LVR[k])//因为前序遍历的首个元素是子树的父节点，该循环在中序遍历中找出该跟结点对应的数组下标k
        k++;
    BintreeNode<T>* p = new BintreeNode<T>(VLR[0]);新建父节点
    if (pRoot == NULL)
        pRoot = p;
    p->pLeftTree = createBintree(VLR + 1, LVR, k);//递归构建左子树
    p->pRightTree = createBintree(VLR + k + 1, LVR + k + 1, n - k - 1);//递归构建右子树
    return p;//返回父节点
}

递归删除算法

这个真没啥好说的，就是跟后序遍历的递归算法几乎一样。

template <class T>
void Bintree<T>::_destroyTree(BintreeNode<T>* p){
    if (p != NULL){
        _destroyTree(p->pLeftTree);
        _destroyTree(p->pRightTree);
        delete p;
    }
}

二叉树遍历的非递归遍历算法

二叉树遍历的递归算法代码非常简洁优美，然而我们需要付出的是效率方面的代价啊。其实把它们改成非递归的算法也不是很难，关键理清楚回退路径，要解决的问题就是何时访问，何时压栈。顺便提一下，线索二叉树虽然很巧妙，但实用性太低，而且对程序猿也很不友好啊，我表示已经被绕晕了╮(╯﹏╰)╭，所以这里就不介绍了。

二叉链表的二叉树

前序遍历

格式化写法：这种写法的好处是好记，容易理清思路，但缺点是还有不少可以优化的点。

template <class T>
void Bintree<T>::preOrder(){
//小p开始了艰险的先序遍历历险记
    BintreeNode<T>* p = pRoot;
    stack<BintreeNode<T>*> s;//辅助栈s
    while (p != NULL || !s.empty()){
        while (p)
        {
          visit(p);
          s.push(p);
          p = p->pLeftTree;//杀入左路子树，见一个就闯进去（visit）并且压栈（丰厚的战利品哦），一直到左子树的底部
        }
        if (!s.empty()){//栈里的东西迟早是要还的哦，就在你到了左路的穷途末路的时候，柳暗花明右一路，继续杀入栈顶节点的右路，当然要留下买路钱咯（弹出栈顶节点呀）(∩_∩)
          p = s.top();
          s.pop();
          p = p->pRightTree;
        }
    }
}

下面是我们数据结构老师（据说是位牛人哦）优化后的算法，分享给大家(^o^)/。
优化的地方在哪呢？大家有没有发现，就在你一路杀入左路的时候，并不是所有节点都需要入栈的哦，
只有左右孩子兼备的时候才需要入栈，只有左孩子或者只有右孩子的话直接进入那一路就ok了，如果两个孩子都没有的话就是叶节点咯，处理跟上面一样。

template <class T>
void Bintree<T>::preOrder(){
    BintreeNode<T>* p = pRoot;
    stack<BintreeNode<T>*> s;
    while (p != NULL)
    {
        visit(p);
        if (p->pLeftTree&&p->pRightTree){
            s.push(p);
            p = p->pLeftTree;
        }
        else if (p->pLeftTree){
            p = p->pLeftTree;
        }
        else if (p->pRightTree){
            p = p->pRightTree;
        }
        else{
            if (!s.empty()){
                p = s.top();
                s.pop();
                p = p->pRightTree;
            }
            else break;
        }
    }
}

中序遍历

格式化写法：

template <class T>
void Bintree<T>::inOrder(){
    BintreeNode<T>* p = pRoot;
    stack<BintreeNode<T>*> s;
    //小p开始了艰险的中序遍历历险记
    while (!s.empty() || p != NULL)
    {
        while (p != NULL){//径直杀入左路，跟前序遍历的区别是不要随便闯入（visit）啊，毕竟是风能进雨能进国王不能进呀，但是一路压栈可是跑不掉的哦。
            s.push(p);
            p = p->pLeftTree;
        }
        if (!s.empty()){//到左路山穷水尽的时候了，怎么办呢，从栈顶弹出一个精灵球（其实是节点），搜刮（visit）这个节点，完了后竟然出现了该节点的右路传送门，果断进去，又是重复如上过程。
            p = s.top();
            s.pop();
            visit(p);
            p = p->pRightTree;
        }
    }
}

优化后的写法：
该写法也是数据结构老师优化的，分享给大家。

template <class T>
void Bintree<T>::inOrder(){
    BintreeNode<T>* p = pRoot;
    stack<BintreeNode<T>*> s;
    while (true)
    {
        while (p)//这个过程还是一路杀入左路，但左路末尾的那个节点是不用进栈的，这里优化了一次入栈。不要怪我抠门咯(*^__^*)
        {
            if (p->pLeftTree){
                s.push(p);
                p = p->pLeftTree;
            }
            else{
                visit(p);
                p = p->pRightTree;
            }
        }
        if (!s.empty()){//这个出栈入右路的过程并没有啥优化的地方。
            p = s.top();
            s.pop();
            visit(p);
            p = p->pRightTree;
        }
        else {
            break;
        }
    }
}

后序遍历

到此，大家可能会觉得，二叉树遍历的非递归算法也不过如此嘛，别急，更大的挑战在后头呢。
如下是格式化写法：
因为后序遍历是访问完左右路才访问父节点的，所有这里让父节点出栈可没那么容易啦。为了方便起见，我用了一个节点辅助栈和一个左右路标记栈，具体过程请欣赏（好吧，小编水平有限，读者就凑合着阅读吧）如下代码+注释。

template <class T>
void Bintree<T>::postOrder(){
    BintreeNode<T>* p = pRoot;
    stack<BintreeNode<T>*> s;
    int tag[100];//这是自定义的一个简陋栈，用于储存左右路标记，左路压入值0，右路压入值1，至于为何不用stl模板类后面有解释哦。
    int top=0;//这是与栈配套使用的栈顶指针
    //小T开始了艰险的后序遍历历险记（为啥不是小p呢？因为最艰巨的任务有我身体力行呀。(*^__^*)
    while (!s.empty()||p!=NULL)
    {
        while (p){//同样的，向左一路杀入到底，这时小T背着两个栈，除了沿途遍历节点要入栈以外，因为是左路，所以要向标志栈压入值0，也是先不要访问节点
            s.push(p);
            tag[++top] = 0;//++的用法大家应该熟知了吧
            p = p->pLeftTree;
        }
        if (!s.empty()){//这里也可以写成while (tag[top] == 1&&!s.empty()),写成这样是因为我想尽量将代码格式化，便于记忆而已。
            while (tag[top] == 1){//把标志栈栈顶为1的节点弹出来，因为父节点的右路已经访问完了，所以随便在退栈以后访问父节点，后序遍历嘛！
                p = s.top();
                s.pop();
                top--;
                visit(p);
            }
        }
        if (!s.empty()){//到了左路的尽头，小T发现标志栈栈顶的节点标志为0，表示该节点的右路可走，那么修改该节点标志为1（以防迷路哦^O^ ），杀入右路去咯，欧耶！
            p = s.top();
            tag[top] = 1;//这里就是为什么用自定义栈的原因，因为stl栈类的数据是封装的，只读不能写，一定要改的话只能将栈顶弹出，修改完后再重新压栈，这样效率远没有直接给栈顶数据赋值的效率高
            p = p->pRightTree;
        }
        else break;//这句必不可少，否则会跳不出循环，因为始终p！=null
    }
}

其实后序遍历还可以优化的，因为左路一路到底最后一个节点是不需要压栈的。

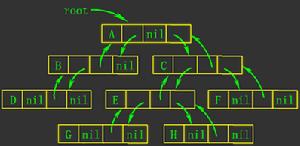
三叉链表的二叉树

三叉链表与二叉链表的主要区别在于，它的结点比二叉链表的结点多一个指针域，该域用于存储一个指向本结点双亲的指针。这样遍历时找回退路径就更加方便了，不需要用栈了，所以这种数据结构的遍历算法效率是最高的，然而要付出的是空间的额外开销，用空间换时间。

前序遍历

先上代码：

template <class T>
void Bintree<T>::preOrder(){
  if (NULL == pRoot) {  
    return ;  
  }  
  BintreeNode<T>* p = pRoot;
  BintreeNode<T>* pr; 
  while (p != NULL) {//不知道大家有没有发现，几乎所有遍历算法首先都是要一路杀入左路
    visit(p); //前序遍历都是走-访节点
    if (p->pLeftTree != NULL) {  
      p = pLeftTree;
    }  
    else if (p->pRightTree != NULL){//左子树到底了，如果有右子树就走右子树
      p = p->pRightTree;
    }  
    else {//左子树到底了，如果 没有右子树就说明到了叶节点了，好，难点来了。
      //关键在于怎么回溯到双亲结点  
      //这个循环是往回查找第一个有没访问过的右子树的父结点
      do {//回溯找爹的操作
        pr = p;  
        p = p->parent;  
      } while (p != NULL && (p->pLeftTree != pr || NULL == pRightTree)); 
      //当p == NULL的时候意味着到达树根了，不能再回溯了
      //当p->pLeftTree == p && p->pRightTree != NULL的时候，就找到了第一个没有被访问的右子树，跳出循环。
      if (p != NULL) {
        p = p->pRightTree;  
      }  
    }  
  }  
}  

中序遍历

template <class T>
void Bintree<T>::inOrder(){
  if (NULL == pRoot) {
    return ;  
  }  
  BintreeNode<T>* p = pRoot;
  BintreeNode<T>* pr;  
  while(NULL != p)  
  {  
    if (p->pLeftTree != NULL) {  
      p = p->pLeftTree;  
    }  
    else {
      visit(p); 
      if (p->pRightTree != NULL) {  
        p =p->pRightTree;  
      }//有没有发现以上的代码有点似曾相识呢，没错它跟前序遍历的代码就差在visit(p);的位置上，这跟也之前的传统而参数的非递归算法几乎一样的，重头戏在于，到达叶节点的回溯找爹的处理上。
      else {  
        //回溯双亲结点，同样是找到第一个没有被访问的右子树  
        //细微的差距就是，因为在递归左子树的过程中，并没有输出双亲结点，所以一旦回溯到父节点时，走之前记得拜访一下这个祖先哦。 
        pr = p;  
        p = p->parent;  
        while (p != NULL && (p->pLeftTree != pr || NULL == p->pRightTree)) {  
          if (p->pLeftTree == pr) {//说明是从左路回溯过来的
            visit(p); //一旦回溯到父节点时，走之前记得拜访一下这个祖先哦。 
          }  
          pr = p;  
          p = p->parent;  
        }
        if (NULL != p) {  
          visit(p); //一旦回溯到父节点时，走之前记得拜访一下这个祖先哦。 
          p = p->pRightTree;  
        }  
      }  
    }  
  }  
}  

后序遍历

template <class T>
void Bintree<T>::postOrder(){
  if (NULL == T) {  
    return ;  
  }  
    BintreeNode<T>* p = pRoot;
    BintreeNode<T>* pr;
  while (p != NULL) {  
    if (p->pLeftTree != NULL){  
      p = p->pLeftTree;
    }  
    else {
      if (p->pRightTree != NULL) {  
        p =p->pRightTree;  
      }
      else {
//到了叶节点后就可以输出当前结点并回溯双亲结点。  
        visit(p);
        pr = p;
        p = p->parent;
        //同样的，利用循环回溯找到第一个右路可走的父节点  
        while(p != NULL && (p->pLeftTree != pr || NULL == p->pRightTree)) {  
          //如果是从右路回溯的话，就说明，这时候的左子树和右子树都被输出了,这时候父结点就应该被访问了。
          if(p->pRightTree == pr || p->pRightTree == NULL) {  
            visit(p);
          }  
          pr = p;  
          p = p->parent;  
        }  
        if(NULL != p) {                      
          p = p->pRightTree;  
        }  
      }              
    }  
  }  
}  

总结

大家有没有发现，非递归的遍历算法并不是那么复杂，相信大家按照思路认真阅读了代码+注释，一定会发现其中的规律。其实算法就只有一个，只是用不同的数据结构或者不同的数据处理方式使代码效率得到了优化。
这么多递归方法有惊人一致的主线—外套一个大循环，大循环内部先套一层小循环，小p沿左路一路到底，若到了左路尽头，跳出小循环；判断右路可走，则走右路；否则就是到达了叶节点，接着处理叶节点（回溯找爹）。
三叉链表的遍历算法和传统的二叉链表的非递归遍历算法的区别就在于二叉链表的非递归遍历算法是用栈实现回溯找爹的过程的，而三叉链表因为本身有一个指向父节点的指针域，回溯找爹方便而且效率高。
前序，中序，后序遍历算法之间的区别在于访问父节点的时机，以此衍生的就是父节点压栈和退栈的时机而已。
(＾－＾)V希望读者读到这儿能会心的说一句，二叉树也不过如此嘛。
其实，这篇是我写的第一篇技术博客，虽然不是什么高大上的东东，但当我看到我竟然不知不觉产出这么多有意义的，好玩的文字，心里真的满满的成就感，希望以后还能有时间和机会去写博客。总结所学，不仅能分享给他人，还能方便自己，提升自己理解的深度，不是吗？(^o^)/YES!

参考的技术博客和文献：
http://blog.csdn.net/sky453589103/article/details/45831105
http://www.cnblogs.com/hicjiajia/archive/2010/08/27/1810055.html
特别鸣谢我的数据结构老师—-杨老师