数据结构：时间复杂度和空间复杂度

时间复杂度和空间复杂度在众多题目中出现频繁，是刷题出现的常规词汇，如经常在某些题目中见到如下要求和限制：

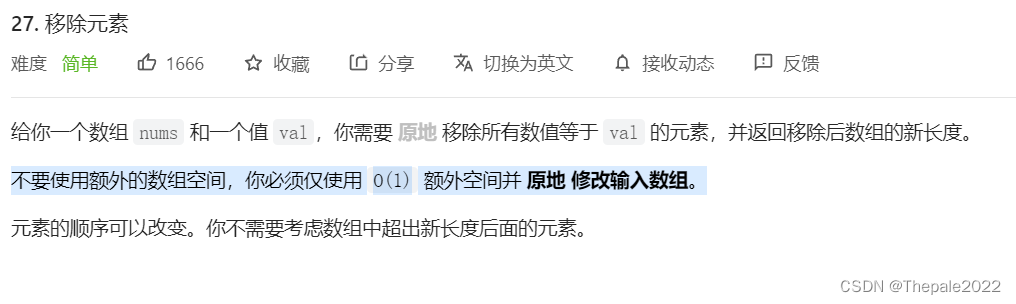
例如以上两道题目，分别对时间复杂度和空间复杂度做出了限制，而对于这两个词的剖析，便成为了本篇文章的重点。 

什么是时间复杂度？

        时间复杂度，并不是用于指定具体时间，例如对一万个数进行排序，一位同学使用冒泡排序实现，但是在高配的电脑上运行，用时1s；而一位同学使用快速排序实现，但是在低配的电脑上运行，用时2s。这时并不能说明冒泡排序算法优于快速排序，因为环境不同，CPU速率不同，以及各个方面的影响都导致了最终时间不一。

        所以我们所需要的，是一种能够衡量程序运行时间优劣，而非具体时间的表示方法，即引出时间复杂度的概念。

让我们看如下代码：

#include <stdio.h>

int main()
{
    int arr[10];

    for(int i = 0; i < 10; ++i)
    {
        arr[i] = i;
    }

    return 0;
}

以上代码的循环体被执行了几次？

答案显而易见，10 次 

#include <stdio.h>

int main()
{
    int n = 0;
    scanf("%d", &n);

    int* parr = malloc(sizeof(int) * n);

    for(int i = 0; i < n; ++i)
    {
        parr[i] = i;
    }

    return 0;
}

这里是让用户输入数字 n，让程序帮我们开辟一个有 n 个元素的 int 数组，并遍历赋值

请问以上程序包含循环体，其运行了几次？

显然，是 n 次，而 n 是随用户所输入的数据量而改变的

    for(int i = 0; i < n; ++i)
    {
        for(int j = 0; j < n; ++j)
        {
            //code...
        }
    }

（以下诸多代码，我只写出循环体，即辨别时间复杂度的部分）

这里的代码又执行了多少次呢？

是 n * n = n ^ 2 次

如果数据量小，或许我们不能看出其中的差别，那么我们对 n 赋不同的值，看看具体执行次数

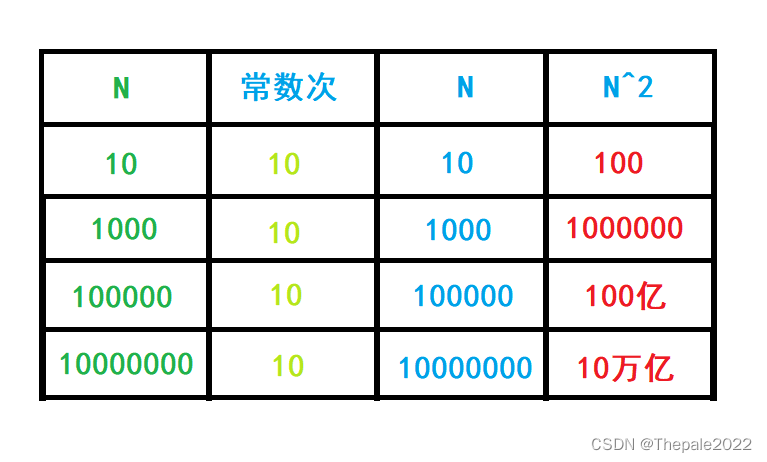
可以看到，如果量级越大，则 N 增大时，变化幅度也越大，所以如果一个题目，能用一个循环 N 次的 for 循环解决，难道你会选择用 N^2 的 for 循环嵌套解决吗？

所以以上三段代码，时间复杂度我们大致可以写为 10，N，N^2

大O渐进表示法 

如果一段代码的时间复杂度是 2N，100N，10000N 呢？那前面的系数对结果的影响到底大吗？这里要注意的是，系数属于常数级别，N 属于一次方级别，即 N 的量级比常数大，我们一般只取对结果影响最大项，可见如下代码：

    for(int i = 0; i < n; i++)
    {
        //code...
    }

    for(int i = 0; i < n; ++i)
    {
        for(int j = 0; j < n; ++j)
        {
            //code...
        }
    }

    for(int i = 0; i < 10; i++)
    {
        //code...
    }

不难得出，其时间复杂度是：N^2 + N + 10

N = 10 时，为 100 + 10 + 10 = 120

N = 100 时，为 10000 + 100 + 10 = 10110

N = 1000 时，为 1000000 + 1000 + 10 = 1001010

可见，量级越小，对结果的影响越小，其结果受影响于最大量级

所以，我们在表示时一般选择忽略低量级，取最大量级

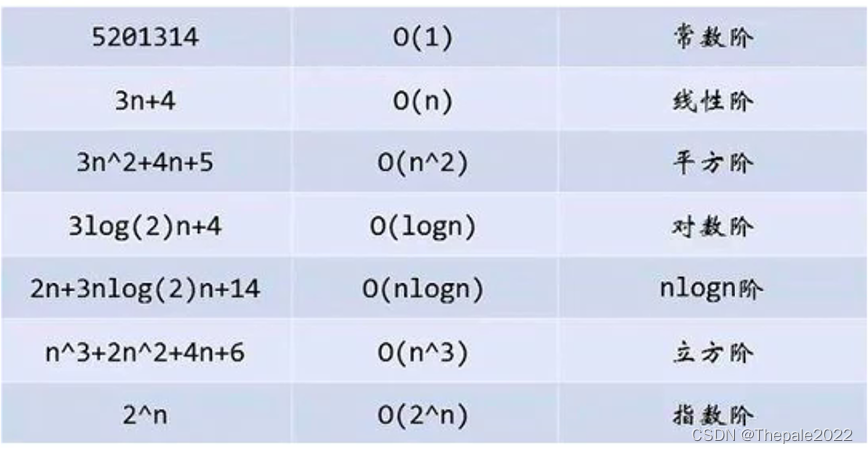
因此，我们引出大O渐进表示法，把 2N 表示为 O(N)；1/2N^2 表示为O(N^2)；10 表示为 O(1)。注意，这里的O(1)并不是表示只运行了一次，而是泛指常数次。

而我们可以看看常见的时间复杂度，随着 N 的增大所要运行次数的变化：

 

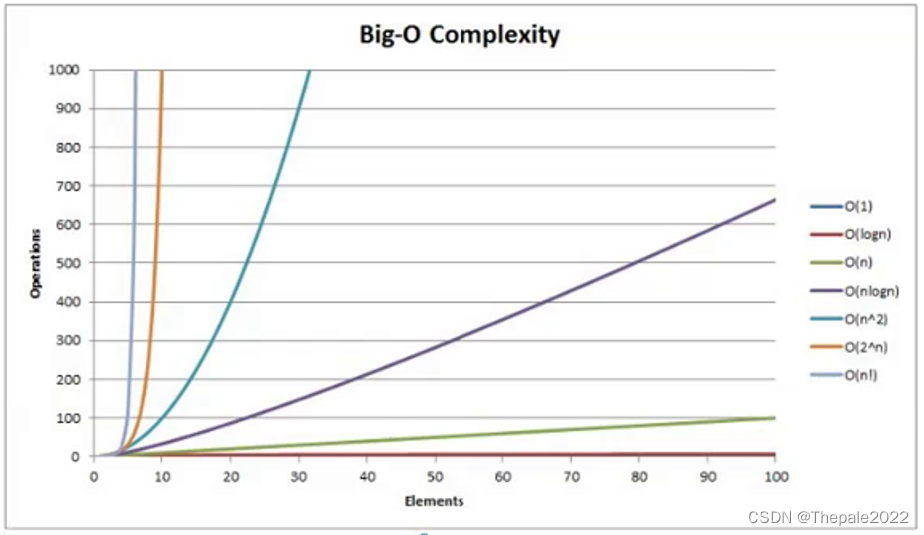
二分查找的时间复杂度剖析

那我们不妨来看一道题：

请在有序的数组中查找一个指定数字，并返回下标。

这时，最容易想到的方法肯定就是 遍历 + 比较。请计算时间复杂度：即 O(N)

但是，有没有更优的方法呢？既然是有序数组，那我们就要运用它的有序特性，引出二分查找的概念 —— 每一次折半查找，大往右，小往左。

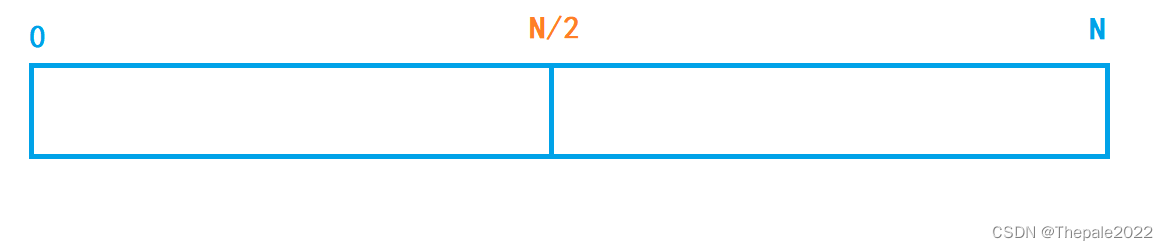
让需要查找的数字与 N / 2 比较，如果比 N / 2 大，则肯定在右半部分，比 N / 2 小，则一定在左半部分。（这里假设一直向左）

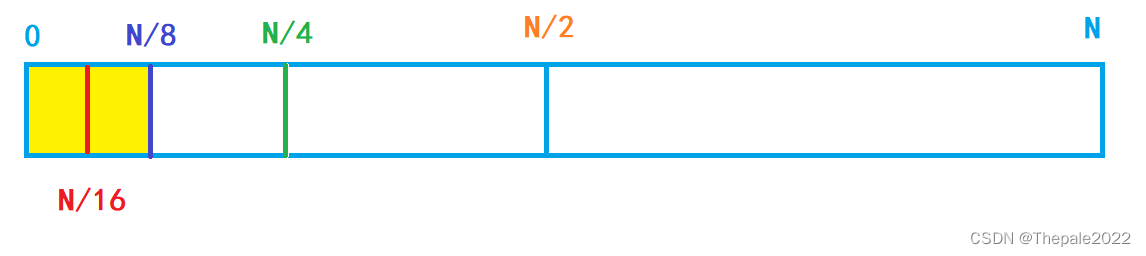
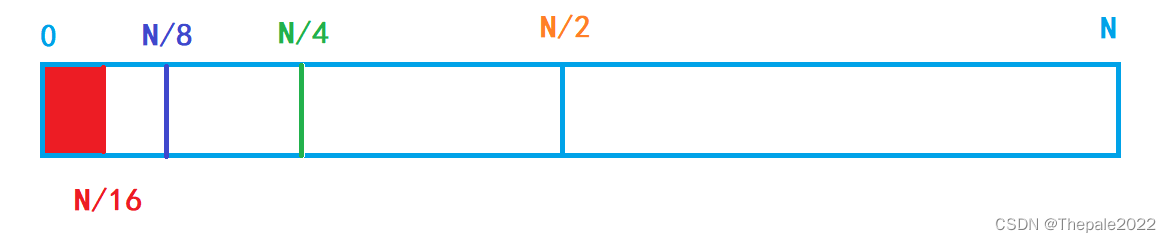 假设剩余的红色为最小元素单位，则 16 个元素我们总共查找了 4 次

这里涉及到一个问题，可不可能我要找的元素刚好就在 N / 2 处呢？也是有可能的，即时间复杂度会有好有坏，那对于以上二分查找，时间复杂度最好为 1 次，即 O(1)；最坏为多少次呢？

这里我们把 N 无限二分，即 N / 2 / 2 / 2... = 1 假设除了 X 次 2

则 2^X = N 即 X = 

 因为不好表示，我们一般把以二为底的对数表示为 logN

即二分排序的最好时间复杂度是：O(1)   最坏时间复杂度是：O(logN)

但我们一般取最坏情况，即总要做好最坏的打算，这个道理想必不用过多阐释。

（这里还涉及到平均复杂度，但一般不会考虑）

递归求解斐波那契数时间复杂度剖析

让我们来回顾一下代码：

int Fib(int n)
{
    if(n < 3) {return 1;}
    
    return Fib(n - 1) + Fib(n - 2);
}

剖析代码是无法直观看出时间复杂度的，我们需要借助图解：

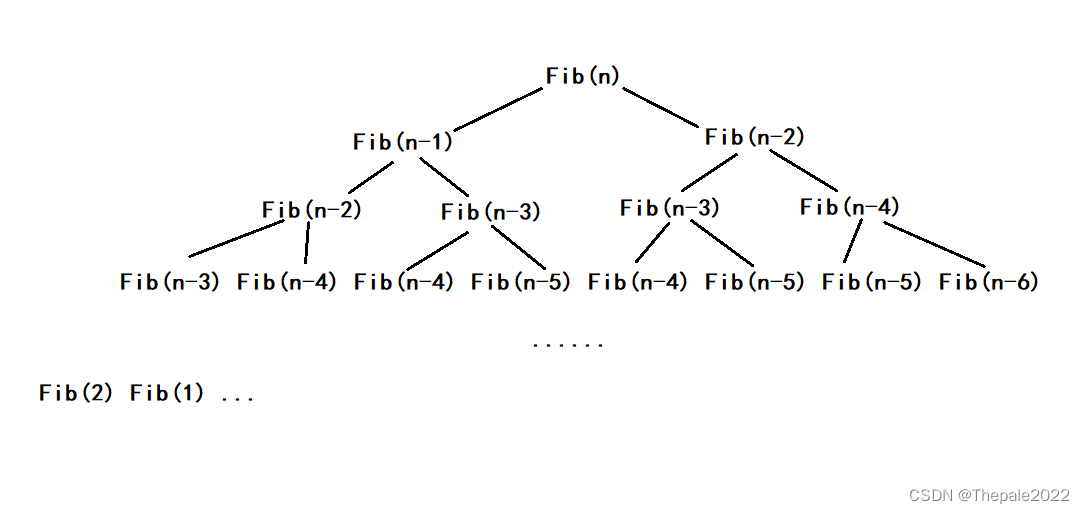
可能这样也无法看出个所以然来，但是请注意每一层的个数：

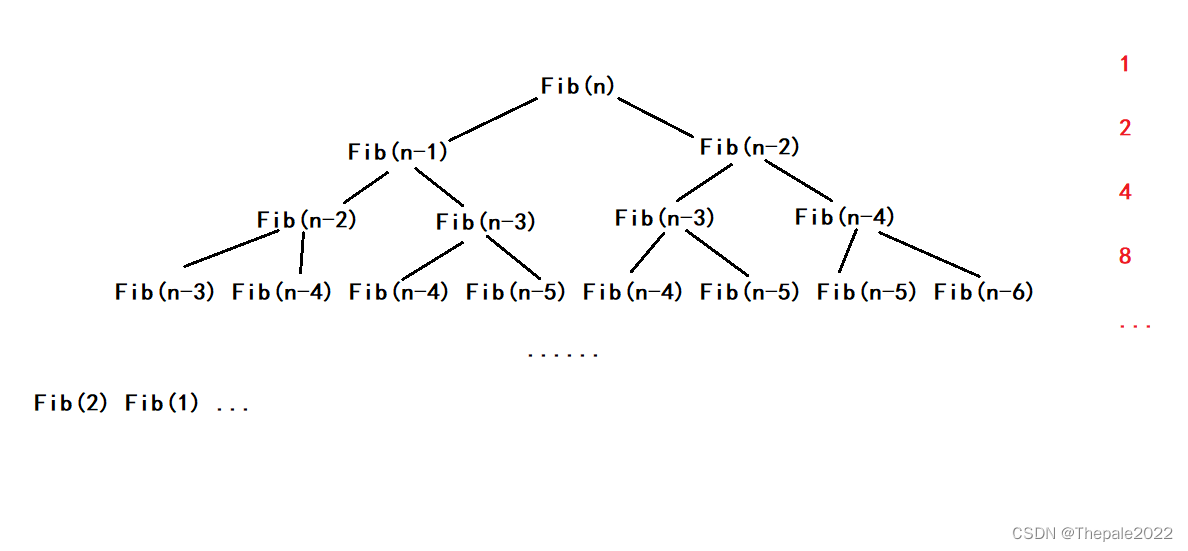 总共有 N 层，而每一层都以 x2 的方式递增，即公比为 2 的等比数列，总共有 N 项

不难得出时间复杂度是：O(2^N) （演算过程请自行计算） 

其时间复杂度在 N 为 30 时， 计算次数直接达到了 10 亿次，可知其递归的弊端；从图中也不难看出，是因为递归进行了大量的重复运算，例如图中方框部分及更多：

 

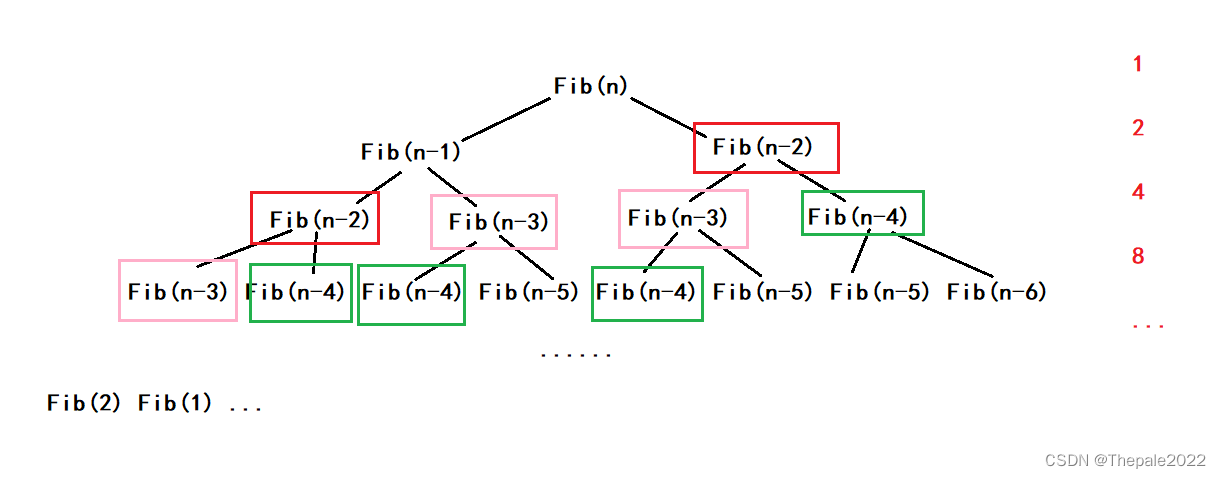
双未知量或多未知量

如果出现以下情况：

for(int i = 0; i < m; ++i)
{
    //code...
}


for(int j = 0; j < n; ++j)
{
    //code...
}

其明面上来说，可能一眼看去，时间复杂度貌似是：O(M + N)

但出现一些特殊情况时：

1.M >> N （注意，一定是远大于）这时可认为 M 量级比 N 大，可忽略 N，时间复杂度变为 O(M)

2.N >> M（注意，一定是远大于）这时可认为 N 量级比 M 大，可忽略 M，时间复杂度变为 O(N)

什么是空间复杂度？

空间复杂度不同于时间复杂度，其是用来衡量开辟物理空间的量，有了时间复杂度的基础，空间复杂度更好理解，且空间复杂度一般而言没有时间复杂度复杂，基本为 O(1)、O(N) 等。

请看以下代码：

for(size_t i = 0; i < 10; ++i)
{
    malloc(sizeof(int));
}

其总共开辟了十次，故空间复杂度为：O(1)

for(size_t i = 0; i < n; ++i)
{
    malloc(sizeof(int));
}

其总共开辟了 N 次，故空间复杂度为：O(N)

对于递归调用也是如此，主要取决于最大压栈数：

void Func(int n)
{
    if(n > 0)
    {
        Func(n - 1);
    }
}

程序执行到 n == 0 时才开始出栈归还申请空间，所以最大压栈数是 N 次，故空间复杂度为：O(N)

递归求解斐波那契数的空间复杂度

很多人的第一反应可能就是：O(2^N)

但是请注意，栈的大小仅为 8M (Linux)，如果进行约 10 亿次压栈，早就 OverFlow 了，但是我们发现，就算输入 100，只是时间久，但程序并没有崩溃，这是为什么呢？

让我们再次分析代码和图解：

int Fib(int n)
{
    if(n < 3) {return 1;}
    
    return Fib(n - 1) + Fib(n - 2);
}

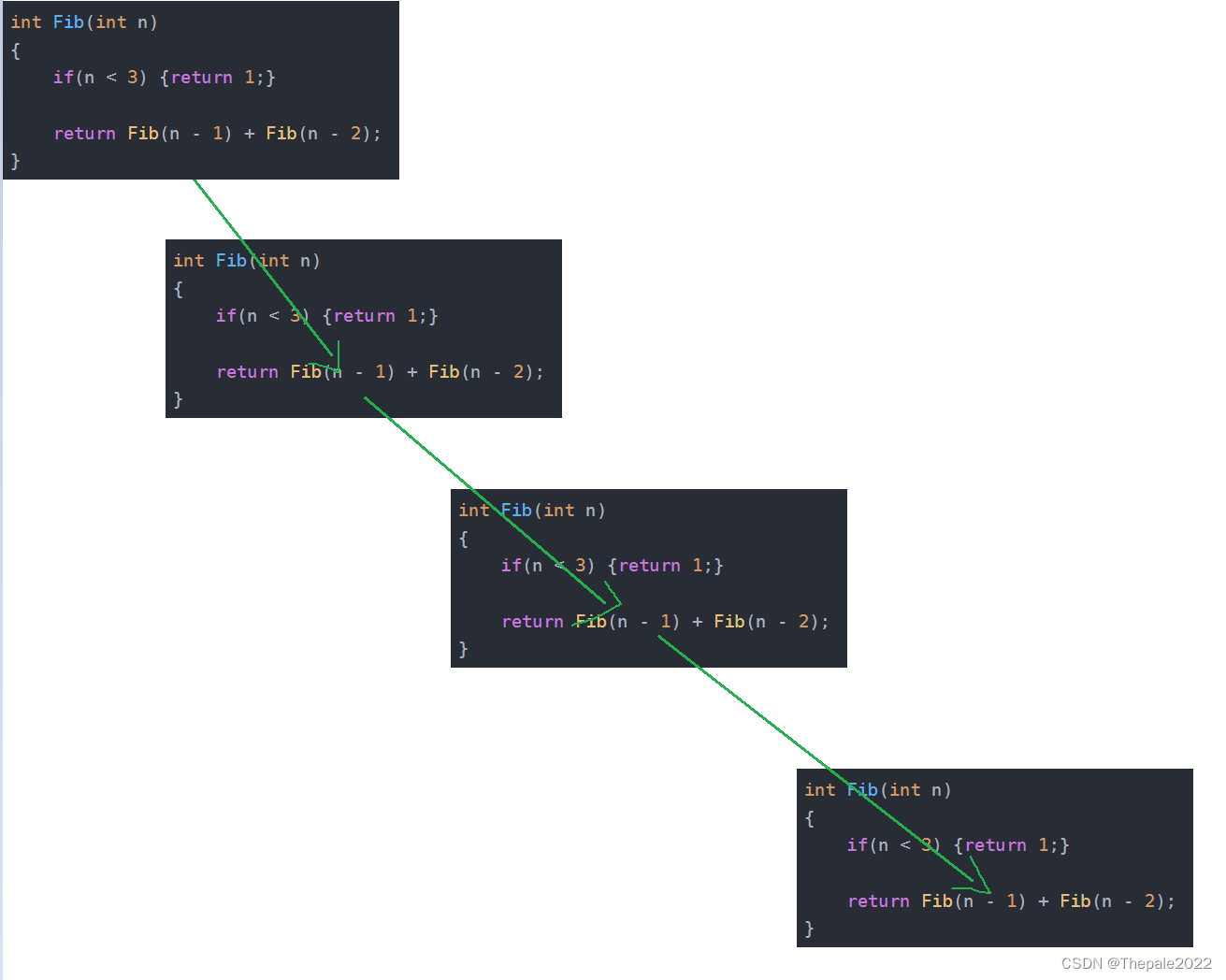
请仔细审视其递归过程：

并不是 Fib(n - 1) 执行后马上去执行 Fib(n - 2)，而是一直向 Fib(n - 1) 执行，直到跳出：

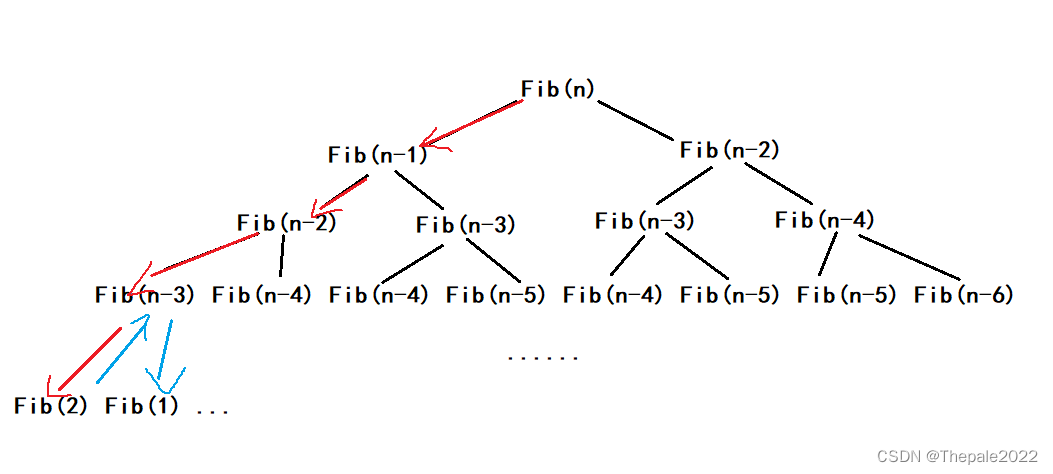所以程序至始至终，最大也就压栈了 N 的空间，其时间复杂度为：O(N)

这也就是为什么，求解斐波那契数虽然时间久，但不会崩溃的原因，因为栈空间没有溢出，程序使用的空间永远没有超过 N

END，望有收获，不吝赐教