【信道编码/Channel Coding】线性分组码

最新推荐文章于 2024-01-24 10:00:00 发布

The Big Tom

最新推荐文章于 2024-01-24 10:00:00 发布

阅读量7.8k

点赞数 11

分类专栏：通信系统文章标签：网络通信编码学线性代数 matlab

本文链接：https://blog.csdn.net/Tomatomatodo/article/details/121905969

版权

通信系统专栏收录该内容

14 篇文章 42 订阅

订阅专栏

简介：

这是本专栏信道编码/Channel Coding的第二站，想对信道编码有一个系统性的认识可以看本专栏的 信道编码的整体框架 一文。而在本篇文章中，将介绍线性分组码的基本原理。

[信道编码/Channel Coding】信道编码的整体框架_Tomatomatodo的博客-CSDN博客信道编码是通信系统中非常重要的一环，它使我们构建的通信系统在一定条件下拥有检错和纠错的能力。而随着历史的演进，信道编码技术在不断地丰富，诞生了许多值得了解学习的编码技术。本篇文章将梳理信道编码的整体框架，旨在让读者对信道编码有一个系统性的认识。而每项技术的细节将在专栏的其他文章中展现。https://blog.csdn.net/Tomatomatodo/article/details/121902663?spm=1001.2014.3001.5501 【信道编码/Channel Coding】纠错编码与差错控制_Tomatomatodo的博客-CSDN博客这是本专栏信道编码/Channel Coding的第一站，想对信道编码有一个系统性的认识可以看本专栏的信道编码的整体框架一文。而在本篇文章中，将介绍如何看一族码字的检错能力以及纠错能力，以及整个传输系统中，我们有什么进行差错控制的方式，这是踏入信道编码的第一步。https://blog.csdn.net/Tomatomatodo/article/details/121903825?spm=1001.2014.3001.5501

4.2 校验矩阵和生成矩阵之间的关系【重要】

五、线性分组码的解码

5.1 标准阵列式解码（最大似然估计）

5.2 伴随式译码

一、线性分组码的性质

1.1 什么是线性

在本专栏的信道编码的整体框架 一文中已经介绍了分组码的数学符号表示了，那么什么是线性分组码呢？用最简单的说法解释就是，所有将k个信息比特映射成n个信息比特的约束关系都是线性的，那么什么是线性的约束关系呢？在二进制的逻辑运算中，异或运算（模二加减）是线性的，但是取反运算是非线性的。

线性分组码有以下重要性质：

全0的信息比特对应的码字也是全0的
C（n，k）是一组码，其中每两个码相模二加减得到的码字依然在这组码中

举个栗子：

Message Segment（信息比特段）	Codeword （码字）
00	11000
01	10101
10	01110
11	00011

上面这个就不是线性分组码。

1.2 可用码组和禁用码组

C（n，k）里，由于k是信息段，而r=n-k的冗余段是用某种约束关系生成的，所以只有 $2^k$ 个可用码，有 $2^n - 2^k$ 个禁用码。

二、矩阵思维看线性分组码

很重要的一个思想就是将 C（n,k）看成是：1xn 的n维向量=1xk 的k维向量在n维空间的映射，这需要一定的线性代数思维，我尽可能简单地解释一下：

首先我们看9单位长的一条线，他是一维的对吧：

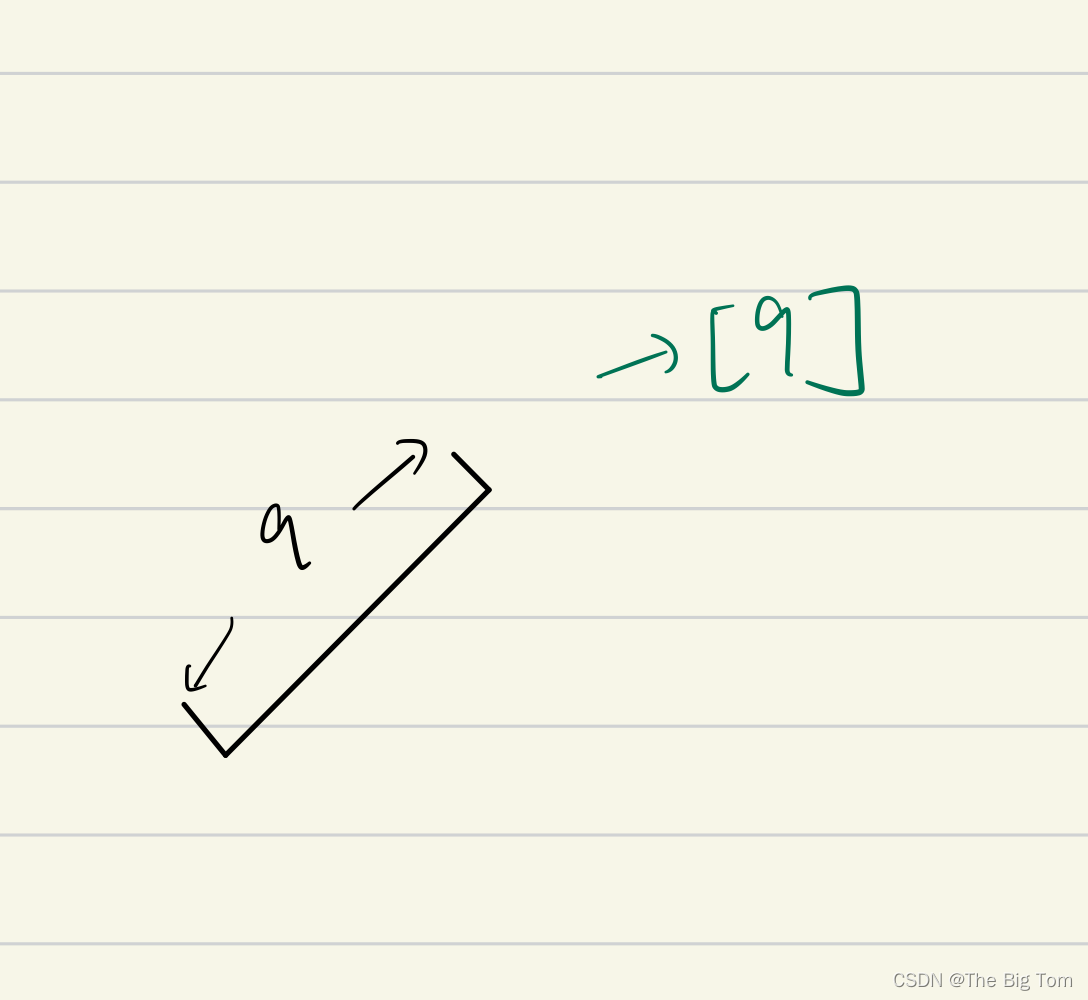
一维的一条线对应矩阵就是一维向量 [9]。

现在我们想将其映射到二维空间去，怎么映射呢？首先要有映射规则，如下图所示：

可以看到，我们选择把它放在一个正交二维坐标系中，而9长的一维向量映射到正交二维坐标系中就是进行投影，所以我们找到了映射关系 [ cos45 sin45 ] ，进行映射后得到一个二维向量。

再进一步，假如我们想将其映射到正交三维坐标系中呢？

可以看到，我们上一步先将一维向量映射到x-y平面中，图中对应蓝色向量映射成粉红色向量。此时我们再将二维向量向三维映射，因为粉红向量本来就在正交三维坐标系上，所以对应的映射关系就是 $\begin{bmatrix} 0 &1 &0 \\ 1 & 0 &0 \end{bmatrix}$ 。

能不能直接从一维映射到三维呢？答案是当然可以：

则a长一维向量对应三维坐标系中每个轴的投影，这个投影关系组成了映射关系（映射矩阵）

所以再重复一下：将 C（n,k）看成是：1xn 的n维向量=1xk 的k维向量在n维空间的映射，那么映射关系就是一个kxn的矩阵。

三、生成矩阵

根据上面所说的，码字向量C是由消息向量m通过kxn的映射关系矩阵生成的。而我们将这个kxn的映射矩阵叫生成矩阵。数学表示就是：

$C=mG$

G就是生成矩阵。

3.1 生成矩阵的系统码

从行列式的基本运算我们可以看到，G的行变换不会改变码字空间（因为没有改变映射关系），所以生成矩阵进行行变换可以变出非常多种G，为了统一，我们引出系统码的说法，也即：将生成矩阵G化简为下面这种形式：

其中 $I_k$ 是kxk的单位矩阵， $P_{kr}$ 是kxr的矩阵，r=n-k

所以有了这种G，我们通过公式 C=mG 就可以算出码字啦！

3.2 MATLAB实现生成码字

%%
clear;clc;
r=3;k=3;n=k+r; % Initialize the parameter of C(n,k)
msg_buffer=[0 0 0;  % Message segments
    0 0 1;
    0 1 0;
    0 1 1;
    1 0 0;
    1 0 1;
    1 1 0;
    1 1 1];
P=[0 1 1;1 0 1;1 1 0];  % P matrix is pre-defined rule
genmat=[P eye(3)];  % Generation Matrix
for i=1:1:8
    msg=msg_buffer(i,:);
    code=encode(msg,n,k,'linear/binary',genmat);
    disp(['The code of ' num2str(msg) ' is ' num2str(code)]);
end

但是兄弟们，G怎么来？P怎么来？往下看就知道了！

四、校验矩阵

若线性分组码中各个码元之间有约束关系，如：

$\left\{\begin{matrix} C_2=C_4\\ C_1=C_3\\ C_0=C_4+C_3 \end{matrix}\right.$

（有人又要问了，约束关系怎么来？这就根据不同的信道编码技术有所不同了,所以我们这里随便写一个线性约束关系）

那么我们进行模二移位之后就会是：

$\begin{Bmatrix} C_2\bigoplus C_4=0\\ C_1\bigoplus C_3=0\\ C_0\bigoplus C_3\bigoplus C_4=0 \end{matrix}$

这不就可以写成：

左边的矩阵就是校验矩阵H，表示某位码元的受约束情况。

即：

$HC^T=0^T$

也即：

$CH^T=0$

4.1 校验矩阵的系统码

和生成矩阵的系统码生成原理一样，将约束关系矩阵H进行行变换化简，使其变为下面的形式：

$H = [ Q_{rk}, I_r]$

4.2 校验矩阵和生成矩阵之间的关系【重要】

仍然用上面所述的矩阵思维看待G和H，kxn 的生成矩阵G的每一行都是k维向量映射到n维向量的规则，然而 nxr 的校验矩阵 $H^T$ 的每一列则是将码元的约束条件，所以如若无差错发生的话，约束条件应该是被满足的，也即 $GH^T=0$

所以：

$G=[I_k ,P_{kr}]=[I_k ,Q_{rk}^T]$

所以我们就得到了P和Q的关系！所以生成矩阵的确定就有眉目了，我们通过不同规则下的约束条件，构造校验矩阵的系统码，再通过Q去求P从而求得生成矩阵G。

五、线性分组码的解码

根据上面的叙述，我们已经知道通过某个约束条件，构造出校验矩阵H和生成矩阵G，然后再用公式 C=mG 生成码字。那么我们怎么解码呢？

5.1 标准阵列式解码（最大似然估计）

最大似然估计简单理解就是就近原则，也就是说，接收端收到一串码字和一族码字所有码比较，离谁近就译成谁。原理很简单，但是有时候会出现出错的码字和表里两个码都相邻的情况（比如最小码距等于2时），所以我们有特别的算法：

1. 由于是线性分组码，一定会有全零码字，我们找禁用码组中和全零码字汉明距离最小的，且1在左边的优先。

2.不断用除全零码字的其他可用码字和这个码字异或获得其他禁用码写在下面

举个栗子：可用码字为0000 0111 1010 1101

则：

	陪集首
可用码字	0000	0111	1010	1101
禁用码字	1000	1111	0010	0101
	0100	0011	1110	1001
	0001	0110	1011	1100

最左边一列则称为陪集首。

比如我接收到了0010，我就会译为1010，接收到1100，我就译为1101

5.2 伴随式译码

假设我们在接收端接收到的码字为 R，则 R = C + E，其中C是码字（无污染），而E是错误图样。打比方说，C=1010001， E=0010000 （意味着第三位错了），那么R=1000001,（经过模二加之后C的第三位变号了，得到R）。

由于：

$CH^T=0$

则在接收端：

$S=RH^T=CH^T+EH^T=0+EH^T=EH^T$

我们称S为伴随式(syndromes)，可以看到S之和E和校验矩阵H有关，和C是无关的。我们整理一下，比如我们再举个的栗子：

Message	Code Vector	Weights
0000	0000000	0
0001	0110001	3
0010	1100010	3
0011	1010011	4
0100	1110100	4
0101	1000101	3
0110	0010110	3
0111	0100111	4
1000	1011000	3
1001	1101001	4
1010	0111010	4
1011	0001011	3
1100	0101100	3
1101	0011101	4
1110	1001110	4
1111	1111111	7

可以看到它的可用码中，最小码距是3，所以它只能纠正一个错误。所以错误图样很简单，就是一位出错的图样。再根据上面给的S的计算公式计算出S。

S（伴随式）	E（错误图样）
000	0000000
011	0000001
110	0000010
111	0000100
101	0001000
001	0010000
010	0100000
100	1000000

可以看到一个S对应一种错误图样，也就意味着哪个比特错了，由于是二元的，非0则1，检测到错误也可以纠正它。

The Big Tom

关注

11
点赞
踩
52

收藏

觉得还不错? 一键收藏
0
评论
【信道编码/Channel Coding】线性分组码

这是本专栏信道编码/Channel Coding的第二站，想对信道编码有一个系统性的认识可以看本专栏的信道编码的整体框架一文。而在本篇文章中，将介绍线性分组码的基本原理。
复制链接

扫一扫