【随机优化】李雅普诺夫优化在通信与排队系统中的应用（第二章）-队列中的引入

【参考书目】Stochastic Network Optimization with Application to Communication and Queueing Systems

【作者】（美）Michael J.Neely---University of Southern California

【出版社】MORGAN&CLAYPOOL PUBLISHERS

目录

速率稳定性（RATE STABILITY）

更强形式的稳定性

速率稳定的随机调度

---

对于每一个时隙t，可以描述未来的状态：

【动态等式】

-----代表一个单一服务者的离散时间队列集合，可以称为队列积压（backlog）

 

 

-----随机的到达（非负）

-----服务的过程（一般为非负，有时可以为负值，尤其是在使用虚拟队列时）

以上单位取决于对应的系统，可以是bit也可以是packet。

【假设】

所以，可得：

继而可以重写上式：

 

-----实际的工作队列，会比原本的b(t)小，被更精确地定义为：

 

且根据定义：

 

动态等式服从于样本路径属性。

 

【引理2.1 (样本路径属性)】

对于以上描述的任何离散时间排队系统，以及对于任何两个时隙t1和t2，使得0≤t1<t2，我们有：

 

所以，对于任意的t>0，我们有：

 

它表明，limt→∞Q ( t ) / t = 0，当且仅当过程a(t)-b(t)↑的时间平均值为零时(其中a(t)-b(t)↑的时间平均值是右侧的极限)。当到达时间平均比率a(t)等于实际出发时间平均比率b(t)时，才会发生这种情况。

 

速率稳定性（RATE STABILITY）

【定义2.2 速率稳定性】

【定义2.3 平均速率稳定性】

 

【定理2.4 (速率稳定性定理)】

假设在以上的Q(t)系统中，所有t的a(t)≥0，所有t的b(t)实值(可能为负值)。假设过程a(t)和b(t)的时间平均值以概率1收敛到有限常数，也就是：

 

则有：

• 当且仅当时，Q(t)为速率稳定
• 如果，则：

 

• 假定有确定的限制：

        Q(t)为平均速率稳定

 

【定理2.5 (速率稳定的必要条件)】

条件同上

如果Q(t)为速率稳定，则有：

如果Q(t)为平均速率稳定，且：

则有：

更强形式的稳定性

速率稳定度和平均速率稳定度仅描述队列中到达和离开的长期平均速率，不要提及队列积压超过某个值的时间比例，也不要提及平均预期积压时间。

【定义2.6 稳态稳定性】

对于任意的M>0，有：

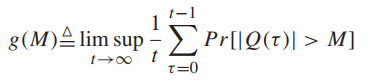
【定义2.7 强稳定性】

【定理2.8 (强稳定性定理)】

条件同上

如果Q(t)是强稳定的，那么：

• Q(t)是稳态稳定的
• 如果有一个有限常数C，使得对于每个t都使下式概率为1：，或者，则Q(t)是速率稳定的，即满足：
• 如果有一个有限常数C，使得对于每个t都使下式概率为1：；或者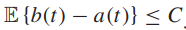，则Q(t)是平均速率稳定的

 

速率稳定的随机调度

速率稳定性定理(定理2.4 )提出了稳定多队列网络的以下简单方法：做出调度决策，以便时间平均服务和到达率得到很好的定义，并满足每个队列I的aiav≤biav。这种方法通常需要对到达和信道概率有完美的了解，以便能够实现期望的时间平均。

 

例子暂略过