中序遍历和后序遍历树构造二叉树
题目
根据中序遍历和后序遍历树构造二叉树
注意事项
你可以假设树中不存在相同数值的节点样例
给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2]
返回如下的树:
题解
由后序遍历定义可知,后序遍历序列的最后一个元素是根节点。
由中序遍历定义可知,可以在中序遍历结果中遍历查找根节点,可将中序遍历序列分为左右子树,这样左右子树的长度也就确定了,在后序遍历序列中,可以确定左右子树的根节点,这样递归下去既可以确定整个树。
/**
* Definition of TreeNode: public class TreeNode { public int val; public
* TreeNode left, right; public TreeNode(int val) { this.val = val; this.left =
* this.right = null; } }
*/
public class Solution
{
/**
* @param inorder
* : A list of integers that inorder traversal of a tree
* @param postorder
* : A list of integers that postorder traversal of a tree
* @return : Root of a tree
*/
public TreeNode buildTree(int[] inorder, int[] postorder)
{
return myBuildTree(inorder, 0, inorder.length - 1, postorder, 0,
postorder.length - 1);
}
private TreeNode myBuildTree(int[] inorder, int instart, int inend,
int[] postorder, int poststart, int postend)
{
if (instart > inend)
{
return null;
}
TreeNode root = new TreeNode(postorder[postend]);
int position = findPosition(inorder, instart, inend,
postorder[postend]);
root.left = myBuildTree(inorder, instart, position - 1, postorder,
poststart, poststart + position - instart - 1);
root.right = myBuildTree(inorder, position + 1, inend, postorder,
poststart + position - instart, postend - 1);
return root;
}
private int findPosition(int[] arr, int start, int end, int key)
{
for (int i = start; i <= end; i++)
{
if (arr[i] == key)
{
return i;
}
}
return -1;
}
}Last Update 2016.10.2








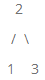














 760
760

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








