Falcon这篇文章发表在PoPETs’20上,论文链接如下:Falcon: Honest-Majority Maliciously Secure Framework for Private Deep Learning。Falcon是一个端到端的三方协议,主要用于机器学习大模型的高效隐私训练和推理。Falcon的主要贡献是:1)解释性强,支持大体量网络架构;2)支持 batch normalization; 3) 在诚实方为主体的恶意环境下,通过 abort 保证安全性;4)高效。
基本原语
Notation
[
[
x
]
]
m
=
(
x
1
,
x
2
,
x
3
)
[\![x]\!]^m=(x_1,x_2,x_3)
[[x]]m=(x1,x2,x3)表示 2-out-of-3 三方冗余秘密分享,
x
≡
x
1
+
x
2
+
x
3
(
m
o
d
m
)
x\equiv x_1+x_2+x_3(\mod m )
x≡x1+x2+x3(modm),
P
1
P_1
P1持有
(
x
1
,
x
2
)
(x_1, x_2)
(x1,x2),
P
2
P_2
P2持有
(
x
2
,
x
3
)
(x_2,x_3)
(x2,x3),
P
3
P_3
P3持有
(
x
3
,
x
1
)
(x_3,x_1)
(x3,x1)。
三个模数:
L
=
2
l
L=2^l
L=2l, 素数
p
p
p, 2。
Basic Operations
Correlated Randomness
3-out-of-3 randomness:
α
1
+
α
2
+
α
3
≡
0
(
m
o
d
L
)
\alpha_1+\alpha_2+\alpha_3\equiv 0(\mod L)
α1+α2+α3≡0(modL),
P
i
P_i
Pi持有随机数
α
i
\alpha_i
αi。
2-out-of-3 randomness:
α
1
+
α
2
+
α
3
≡
0
(
m
o
d
L
)
\alpha_1+\alpha_2+\alpha_3\equiv 0(\mod L)
α1+α2+α3≡0(modL),
P
i
P_i
Pi持有随机数
(
α
i
,
α
i
+
1
)
(\alpha_i,\alpha_{i+1})
(αi,αi+1)。
Linear operations
假设 a , b , c a, b, c a,b,c是常数, [ [ x ] ] m , [ [ y ] ] m [\![x]\!]^m, [\![y]\!]^m [[x]]m,[[y]]m是秘密分享,那么 [ [ a x + b y + c ] ] m [\![ax+by+c]\!]^m [[ax+by+c]]m可以通过本地计算 ( a x 1 + b y 1 + c , a x 2 + b y 2 , a x 3 + b y 3 ) (ax_1+by_1+c, ax_2+by_2,ax_3+by_3) (ax1+by1+c,ax2+by2,ax3+by3)实现。
Multiplications
假设 [ [ x ] ] m = ( x 1 , x 2 , x 3 ) , [ [ y ] ] m = ( y 1 , y 2 , y 3 ) [\![x]\!]^m=(x_1,x_2,x_3), [\![y]\!]^m=(y_1,y_2,y_3) [[x]]m=(x1,x2,x3),[[y]]m=(y1,y2,y3), 各方本地计算 z 1 = x 1 y 1 + x 2 y 1 + x 1 y 2 , z 2 = x 2 y 2 + x 3 y 2 + x 2 y 3 , z 3 = x 3 y 3 + x 1 y 3 + x 3 y 1 z_1=x_1y_1+x_2y_1+x_1y_2, z_2=x_2y_2+x_3y_2+x_2y_3, z_3=x_3y_3+x_1y_3+x_3y_1 z1=x1y1+x2y1+x1y2,z2=x2y2+x3y2+x2y3,z3=x3y3+x1y3+x3y1, z 1 , z 2 , z 3 z_1,z_2,z_3 z1,z2,z3组成 [ [ z = x ⋅ y ] ] m [\![z=x\cdot y]\!]^m [[z=x⋅y]]m 的3-out-of-3秘密分享。
Reconstruction
在半诚实模式下, P i P_i Pi发送 x i x_i xi给 P i + 1 P_{i+1} Pi+1;在恶意模式下, P i P_i Pi发送 x i x_i xi给 P i + 1 P_{i+1} Pi+1,发送 x i + 1 x_{i+1} xi+1给 P i − 1 P_{i-1} Pi−1,当二者不一致时abort。
Select Shares
输入为随机值
[
[
x
]
]
L
,
[
[
y
]
]
L
[\![x]\!]^L, [\![y]\!]^L
[[x]]L,[[y]]L 和随机比特
b
b
b, 输出
[
[
z
]
]
L
[\![z]\!]^L
[[z]]L取决于
b
b
b。
具体实现为:生成随机比特
[
[
c
]
]
2
,
[
[
c
]
]
L
[\![c]\!]^2, [\![c]\!]^L
[[c]]2,[[c]]L, 公开
e
=
(
b
⊕
c
)
e=(b\oplus c)
e=(b⊕c)。 当
e
=
1
e=1
e=1时,
[
[
d
]
]
L
=
[
[
1
−
c
]
]
L
[\![d]\!]^L=[\![1-c]\!]^L
[[d]]L=[[1−c]]L; 当
e
=
0
e=0
e=0时,
[
[
d
]
]
L
=
[
[
c
]
]
L
[\![d]\!]^L=[\![c]\!]^L
[[d]]L=[[c]]L;
[
[
z
]
]
L
=
[
[
(
y
−
x
)
⋅
d
]
]
L
+
[
[
x
]
]
L
[\![z]\!]^L=[\![(y-x)\cdot d]\!]^L+[\![x]\!]^L
[[z]]L=[[(y−x)⋅d]]L+[[x]]L。
可以看到,当
b
=
0
b=0
b=0时,
d
=
0
,
[
[
z
]
]
L
=
[
[
x
]
]
L
d=0, [\![z]\!]^L=[\![x]\!]^L
d=0,[[z]]L=[[x]]L; 当
b
=
1
b=1
b=1时,
d
=
1
,
[
[
z
]
]
L
=
[
[
y
]
]
L
d=1, [\![z]\!]^L=[\![y]\!]^L
d=1,[[z]]L=[[y]]L。
XOR with public bit b
给定 [ [ x ] ] m , b [\![x]\!]^m, b [[x]]m,b, [ [ y ] ] m = [ [ x ⊕ b ] ] m [\![y]\!]^m=[\![x\oplus b]\!]^m [[y]]m=[[x⊕b]]m可以通过本地计算 y = x + b − 2 b ⋅ x y=x+b-2b\cdot x y=x+b−2b⋅x实现。
Evaluating [ [ ( − 1 ) β ⋅ x ] ] m [\![(-1)^\beta\cdot x]\!]^m [[(−1)β⋅x]]m
假设 β ∈ { 0 , 1 } , [ [ ( − 1 ) β ⋅ x ] ] m = [ [ ( 1 − 2 β ) ⋅ x ] ] m \beta\in\{0,1\}, [\![(-1)^\beta\cdot x]\!]^m=[\![(1-2\beta)\cdot x]\!]^m β∈{0,1},[[(−1)β⋅x]]m=[[(1−2β)⋅x]]m
核心模块
Private Compare

Π
P
C
\Pi_{PC}
ΠPC计算
x
≥
r
x\geq r
x≥r, 其中
x
∈
Z
p
,
r
x\in\mathbb{Z}_p, r
x∈Zp,r是公开的比特。
β
\beta
β起到盲化作用,第二步可以用
(
1
−
2
β
)
⋅
(
x
[
i
]
−
r
[
i
]
)
(1-2\beta)\cdot (x[i]-r[i])
(1−2β)⋅(x[i]−r[i])计算,做乘法需要一次交互;第六步乘法需要
l
o
g
2
l
+
1
log_2^l+1
log2l+1次交互。在
x
,
r
x,r
x,r不相同的最高比特位置
t
t
t,当
x
≥
r
x\geq r
x≥r时,假设
β
=
0
\beta=0
β=0, 那么
x
[
t
]
−
r
[
t
]
=
1
x[t]-r[t]=1
x[t]−r[t]=1, 由于
w
[
t
]
=
1
,
c
[
i
]
≥
1
w[t]=1, c[i]\geq 1
w[t]=1,c[i]≥1恒成立,因此
d
=
1
,
β
′
=
1
d=1,\beta'=1
d=1,β′=1; 假设
β
=
1
,
c
[
t
]
=
0
,
d
=
0
,
β
′
=
0
\beta=1, c[t]=0, d=0, \beta'=0
β=1,c[t]=0,d=0,β′=0。对于
x
<
r
x<r
x<r也可以推导出正确结果。
Wrap Function
w
r
a
p
wrap
wrap是为了计算进位,定义如下:
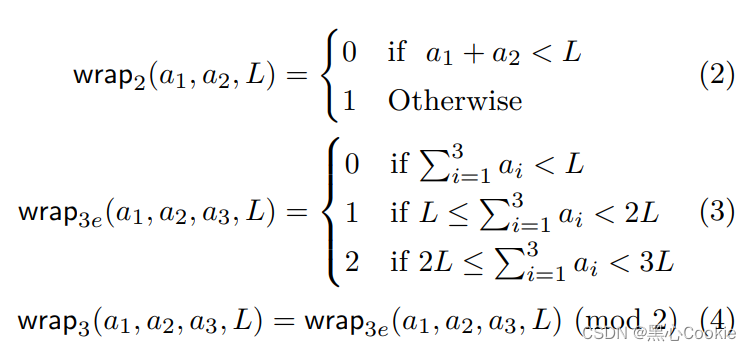
为了计算
w
r
a
p
3
wrap_3
wrap3, 引入一个随机数掩膜
x
x
x,并分享在
a
a
a中,对于秘密值
a
a
a有:
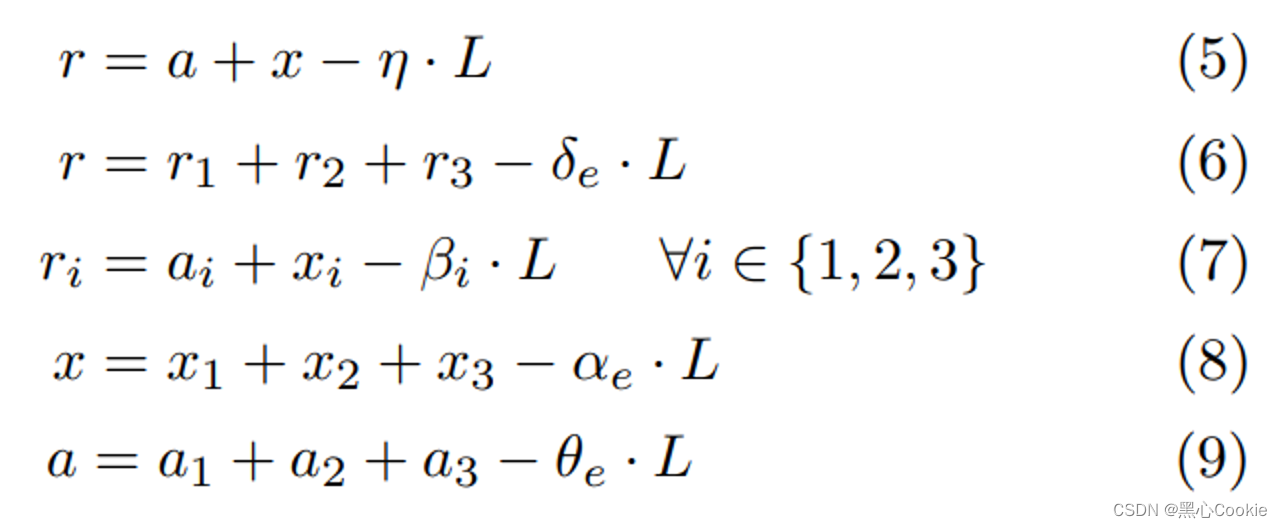
(
5
)
−
(
6
)
−
(
7
)
+
(
8
)
+
(
9
)
(5)-(6)-(7)+(8)+(9)
(5)−(6)−(7)+(8)+(9)得到
θ
e
=
β
1
+
β
2
+
β
3
+
δ
e
−
η
−
α
e
\theta_e=\beta_1+\beta_2+\beta_3+\delta_e-\eta-\alpha_e
θe=β1+β2+β3+δe−η−αe;
模2得到
θ
=
β
1
+
β
2
+
β
3
+
δ
−
η
−
α
\theta=\beta_1+\beta_2+\beta_3+\delta-\eta-\alpha
θ=β1+β2+β3+δ−η−α。

ReLU and Derivative of ReLU
DReLU定义: L / 2 L/2 L/2是0-63位,最高位为1,其余位为0的数,当 x > L / 2 x>L/2 x>L/2时, x x x的 MSB 为1,根据最高位表示符号的原则,说明 x x x为负数, 对应 ReLU 的负数部分,因此为 0;反之对应 ReLU 的正数部分,导数为1。
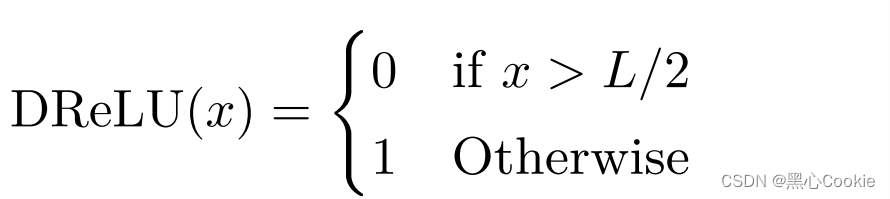
给定
a
=
a
1
+
a
2
+
a
3
(
m
o
d
L
)
a=a_1+a_2+a_3(\mod L)
a=a1+a2+a3(modL), 有
M
S
B
(
a
)
=
M
S
B
(
a
1
)
+
M
S
B
(
a
2
)
+
M
S
B
(
a
3
)
+
c
(
m
o
d
2
)
MSB(a)=MSB(a_1)+MSB(a_2)+MSB(a_3)+c(\mod 2)
MSB(a)=MSB(a1)+MSB(a2)+MSB(a3)+c(mod2)
注意到
D
R
e
L
U
(
a
)
=
1
−
M
S
B
(
a
)
DReLU(a)=1-MSB(a)
DReLU(a)=1−MSB(a), 因此
D
R
e
L
U
(
a
)
=
M
S
B
(
a
1
)
⊕
M
S
B
(
a
2
)
⊕
M
S
B
(
a
3
)
⊕
w
r
a
p
3
(
2
a
1
,
2
a
2
,
2
a
3
,
L
)
⊕
1
DReLU(a)=MSB(a_1)\oplus MSB(a_2)\oplus MSB(a_3)\oplus wrap_3(2a_1,2a_2,2a_3,L)\oplus 1
DReLU(a)=MSB(a1)⊕MSB(a2)⊕MSB(a3)⊕wrap3(2a1,2a2,2a3,L)⊕1
计算
Π
\Pi
Π即可得到激活函数结果。

Maxpool and Derivative of Maxpool
Maxpool 是输入一个向量,输出最大值,可以用一个同样 size 的 one-hot 向量实现,其中的比较部分与 ReLU 一致。

Division
除法利用近似计算,首先计算除数的指数,即
2
α
≤
x
<
2
α
+
1
2^\alpha\leq x<2^{\alpha+1}
2α≤x<2α+1中的
α
\alpha
α,算法如下:

step4中,c=1 表示
x
−
2
2
i
+
α
≥
0
x-2^{2^i+\alpha}\ge 0
x−22i+α≥0。
得到
α
\alpha
α 进行如下计算:

本文采用Newton-Raphson算法近似计算
a
/
b
a/b
a/b。参考师兄的文章:Falcon。
Batch Normalization
套用除法算法,也采用近似算法。

























 2073
2073

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








