BLAZE: Blazing Fast Privacy-Preserving Machine Learning阅读笔记
简介
本文介绍BLAZE这篇文章,BLAZE是Arpita Patra等人发表于NDSS’20上的文章《BLAZE: Blazing Fast Privacy-preserving Machine Learning》, 论文链接如下:BLAZE: Blazing Fast Privacy-preserving Machine Learning
BLAZE在安全外包环境下,构建了一个三方服务器、可抵御一个恶意敌手的PPML框架,协议是在
Z
2
l
\mathcal{Z}_{2^l}
Z2l整数环上实现的。
BLAZE框架由三层架构实现,第一层是最底层的协议:乘法协议、比特提取协议和Bit2A转换协议;第二层由第一层搭建:点积运算、截断、ReLU和Sigmoid激活函数;第三层是应用:线性回归、逻辑回归和神经网络。
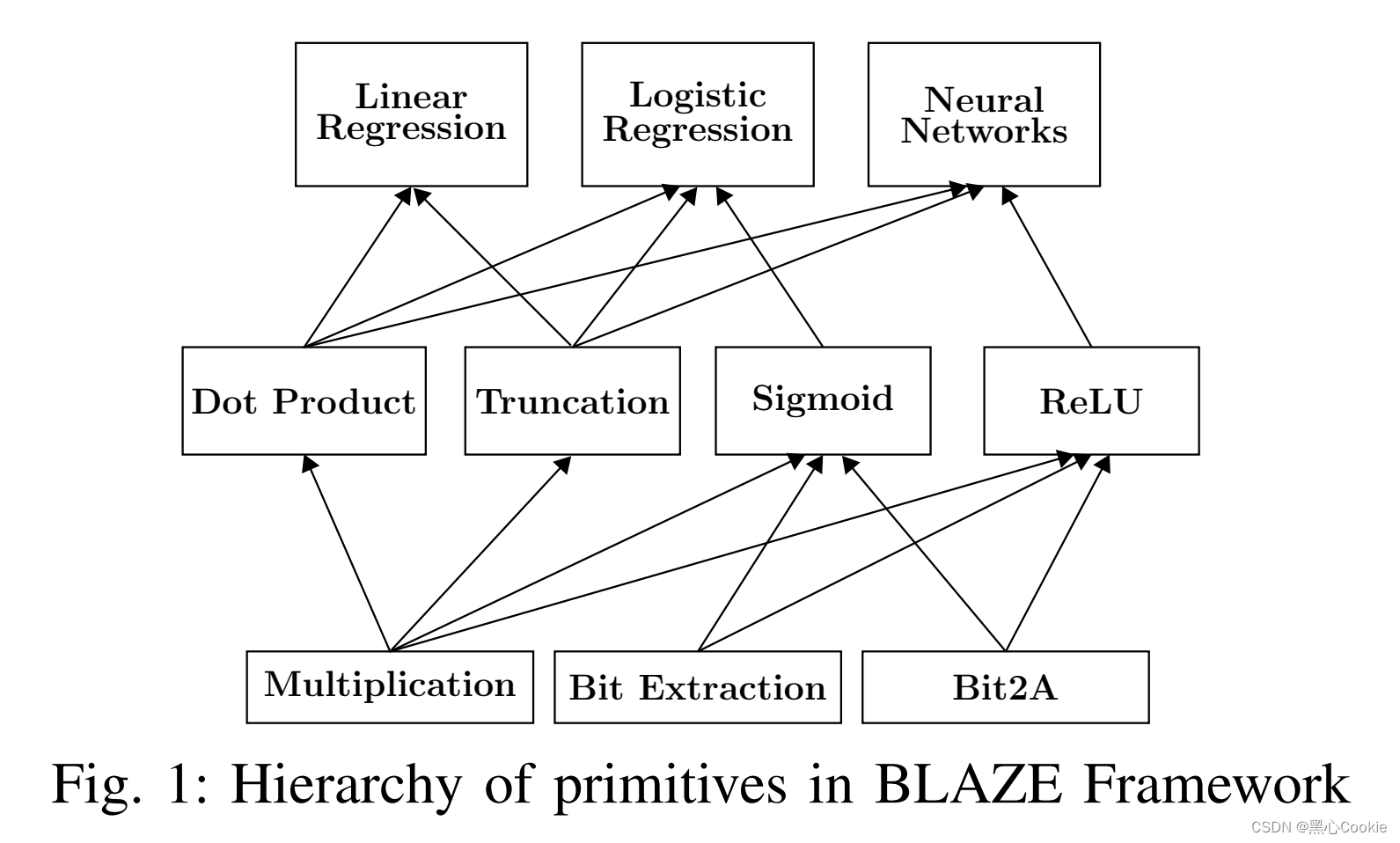
BLAZE的核心是秘密分享的构造和乘法的设计,其他运算都是建立在乘法的基础上,因此本文主要介绍分享重构过程和乘法协议。
秘密分享
Sharing语义
三种秘密分享 (秘密值为 v v v):
- [ ⋅ ] − s h a r i n g [\cdot ]-sharing [⋅]−sharing: P 1 , P 2 P_1, P_2 P1,P2分别持有 [ v ] 1 , [ v ] 2 ∈ Z 2 l [v]_1,[v]_2\in \mathcal{Z}_{2^l} [v]1,[v]2∈Z2l, 且 v = [ v ] 1 + [ v ] 2 v=[v]_1+[v]_2 v=[v]1+[v]2.
- ⟨ ⋅ ⟩ − s h a r i n g \langle\cdot\rangle-sharing ⟨⋅⟩−sharing: P 0 P_0 P0持有 ( [ λ v ] 1 , [ λ v ] 2 ) ([\lambda_v]_1,[\lambda_v]_2) ([λv]1,[λv]2), P 1 P_1 P1持有 ( [ λ v ] 1 , v + λ v ] ) ([\lambda_v]_1, v+\lambda_v]) ([λv]1,v+λv]), P 2 P_2 P2持有 ( [ λ v ] 2 , v + λ v ] ) ([\lambda_v]_2, v+\lambda_v]) ([λv]2,v+λv]), 其中 [ λ v ] 1 , [ λ v ] 2 ∈ Z 2 l , λ v = [ λ v ] 1 + [ λ v ] 2 [\lambda_v]_1, [\lambda_v]_2 \in \mathbb{Z}_{2^l}, \lambda_v=[\lambda_v]_1+[\lambda_v]_2 [λv]1,[λv]2∈Z2l,λv=[λv]1+[λv]2.
-
[
[
⋅
]
]
−
s
h
a
r
i
n
g
[\![\cdot]\!]-sharing
[[⋅]]−sharing: 在
⟨
⋅
⟩
−
s
h
a
r
i
n
g
\langle\cdot\rangle-sharing
⟨⋅⟩−sharing的基础上,新增加一个
γ
∈
Z
2
l
\gamma\in\mathbb{Z}_{2^l}
γ∈Z2l, 其中
P
1
,
P
2
P_1, P_2
P1,P2 持有
γ
v
\gamma_v
γv,
P
0
P_0
P0 持有
β
v
+
γ
v
\beta_v+\gamma_v
βv+γv.

Sharing Protocol
Protocol
Π
s
h
(
P
i
,
v
)
\Pi_{sh}(P_i,v)
Πsh(Pi,v) : server
P
i
P_i
Pi 生成秘密值
v
∈
Z
2
l
v\in \mathbb{Z}_{2^l}
v∈Z2l的
[
[
⋅
]
]
−
s
h
a
r
i
n
g
[\![\cdot]\!]-sharing
[[⋅]]−sharing .

预处理阶段 i=0,1,2 时三方持有信息:

在线阶段 i=0,1,2 时三方操作:

Protocol
Π
j
s
h
(
P
i
,
P
j
,
v
)
\Pi_{jsh}(P_i,P_j,v)
Πjsh(Pi,Pj,v) :servers
P
i
,
P
j
P_i, P_j
Pi,Pj 联合生成秘密值
v
∈
Z
2
l
v\in \mathbb{Z}_{2^l}
v∈Z2l的
[
[
⋅
]
]
−
s
h
a
r
i
n
g
[\![\cdot]\!]-sharing
[[⋅]]−sharing.

对于不同输入,
Π
j
s
h
(
P
i
,
P
j
,
v
)
\Pi_{jsh}(P_i,P_j,v)
Πjsh(Pi,Pj,v)的输出结果,其中最后一行的每一个三元组对应的值分别是
P
0
:
(
[
α
v
]
1
,
[
α
v
]
2
,
β
v
+
γ
v
)
;
P
1
:
(
[
α
v
]
1
,
β
v
=
v
+
α
v
,
γ
v
)
;
P
2
:
(
[
α
v
]
2
,
β
v
=
v
+
α
v
,
γ
v
)
P_0: ([\alpha_v]_1, [\alpha_v]_2,\beta_v+\gamma_v); P_1:([\alpha_v]_1, \beta_v=v+\alpha_v,\gamma_v); P_2:([\alpha_v]_2, \beta_v=v+\alpha_v,\gamma_v)
P0:([αv]1,[αv]2,βv+γv);P1:([αv]1,βv=v+αv,γv);P2:([αv]2,βv=v+αv,γv).

Protocol
Π
r
e
c
(
P
,
[
[
v
]
]
)
\Pi_{rec}(\mathcal{P},[\![v]\!])
Πrec(P,[[v]]) :
P
\mathcal{P}
P 重构秘密值
v
v
v.

Multiplication
Protocol Π m u l t ( P , [ [ x ] ] , [ [ y ] ] ) \Pi_{mult}(\mathcal{P}, [\![x]\!],[\![y]\!]) Πmult(P,[[x]],[[y]]) : 给定 x x x 和 y y y的 [ [ ⋅ ] ] − s h a r i n g [\![\cdot]\!]-sharing [[⋅]]−sharing, P \mathcal{P} P 计算 z = x y z =xy z=xy的 [ [ ⋅ ] ] − s h a r i n g [\![\cdot]\!]-sharing [[⋅]]−sharing .
半诚实敌手模式
-
β z = z + α z = x y + α z = ( β x − α x ) ( β y − α y ) + α z = β x β y − β x α y − β y α x + α x α y + α z \beta_z=z+\alpha_z=xy+\alpha_z=(\beta_x-\alpha_x)(\beta_y-\alpha_y)+\alpha_z=\beta_x\beta_y-\beta_x\alpha_y-\beta_y\alpha_x+\alpha_x\alpha_y+\alpha_z βz=z+αz=xy+αz=(βx−αx)(βy−αy)+αz=βxβy−βxαy−βyαx+αxαy+αz
-
预处理阶段: P 0 , P j , j ∈ { 1 , 2 } P_0, P_j, j \in\{1,2\} P0,Pj,j∈{1,2} 随机采样 [ α z ] j ∈ Z 2 l [\alpha_z]_j\in\mathbb{Z}_{2^l} [αz]j∈Z2l, P 1 , P 2 P_1, P_2 P1,P2 随机采样 γ z ∈ Z 2 l \gamma_z\in\mathbb{Z}_{2^l} γz∈Z2l. P 0 P_0 P0 本地计算 Γ x y = α x α y \Gamma_{xy}=\alpha_x\alpha_y Γxy=αxαy 并生成相应的 [ ⋅ ] − s h a r i n g [\cdot]-sharing [⋅]−sharing. Servers P 1 , P 2 P_1, P_2 P1,P2 本地计算 [ β z ] j = ( j − 1 ) β x β y − β x [ α y ] j − β y [ α x ] j + [ Γ x y ] j + [ α z ] j [\beta_z]_j=(j-1)\beta_x\beta_y-\beta_x[\alpha_y]_j-\beta_y[\alpha_x]_j+[\Gamma_{xy}]_j+[\alpha_z]_j [βz]j=(j−1)βxβy−βx[αy]j−βy[αx]j+[Γxy]j+[αz]j.
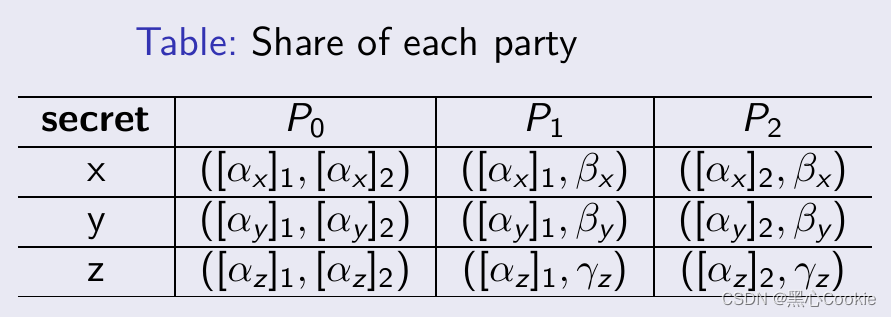
-
在线阶段: P 1 , P 2 P_1, P_2 P1,P2 交换它们的秘密值并重构 β z \beta_z βz. P 1 P_1 P1 计算并发送 β z + γ z \beta_z+\gamma_z βz+γz 给 P 0 P_0 P0.
恶意敌手模式
原有的乘法协议存在三个问题:
- 问题一:当 P 0 P_0 P0被腐败,那么 P 0 P_0 P0在预处理阶段产生的 Γ x y \Gamma_{xy} Γxy的秘密分享值可能是错误的,即 Γ x y ≠ α x α y \Gamma_{xy}\neq\alpha_x\alpha_y Γxy=αxαy.
- 问题二:当 P 1 P_1 P1(或 P 2 P_2 P2)被腐败, 那么在线阶段交给诚实的另一方的 [ β z ] j [\beta_z]_j [βz]j可能是错误的,从而导致重构出错误的 β z \beta_z βz.
- 问题三:当 P 1 P_1 P1被腐败,那么在线阶段交给 P 0 P_0 P0的 β z + γ z \beta_z+\gamma_z βz+γz可能是错误的。
解决方案:
- 问题一:前面的乘法协议中,我们其实并没有充分利用三方拥有的所有信息,事实上,三方拥有的所有信息是这样的:

因此,我们构造一个
χ
=
γ
x
α
y
+
γ
y
α
x
−
Γ
x
y
+
ψ
\chi=\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi
χ=γxαy+γyαx−Γxy+ψ, 其中,
ψ
∈
Z
2
l
\psi\in\mathbb{Z}_{2^l}
ψ∈Z2l是由
P
1
,
P
2
P_1, P_2
P1,P2随机采样生成的随机数.
服务器
P
j
,
j
∈
{
1
,
2
}
P_j,j\in\{1,2\}
Pj,j∈{1,2} 在本地计算
[
χ
]
j
=
γ
x
[
α
y
]
j
+
γ
y
[
α
x
]
j
−
[
Γ
x
y
]
j
+
[
ψ
]
j
[\chi]_j = \gamma_x[\alpha_y]_j+\gamma_y[\alpha_x]_j-[\Gamma_{xy}]_j+[\psi]_j
[χ]j=γx[αy]j+γy[αx]j−[Γxy]j+[ψ]j 并将其发送给
P
0
P_0
P0,
P
0
P_0
P0计算得到
χ
=
[
χ
]
1
+
[
χ
]
2
\chi=[\chi]_1+[\chi]_2
χ=[χ]1+[χ]2.
令
d
=
γ
x
−
α
x
,
e
=
γ
y
−
α
y
,
f
=
(
γ
x
γ
y
+
ψ
)
−
χ
d=\gamma_x-\alpha_x, e=\gamma_y-\alpha_y,f=(\gamma_x\gamma_y+\psi)-\chi
d=γx−αx,e=γy−αy,f=(γxγy+ψ)−χ, 当且仅当
χ
\chi
χ 计算正确时,满足
f
=
d
e
f=de
f=de.
假如
P
0
P_0
P0产生错误的
Γ
x
y
\Gamma_{xy}
Γxy, 可以记作
Γ
x
y
+
Δ
\Gamma_{xy}+\Delta
Γxy+Δ, 那么
d
e
=
f
+
Δ
≠
f
de=f+\Delta\neq f
de=f+Δ=f.
为了保证
χ
\chi
χ 的正确性,需要确保
(
d
,
e
,
f
)
(d,e,f)
(d,e,f)是一个有效的三元组,因此文章构造了一个新的协议
Π
m
u
l
Z
K
(
P
,
d
,
e
)
\Pi_{mulZK}(\mathcal{P},d,e)
ΠmulZK(P,d,e)来产生三元组。

通过该协议,构造的
d
,
e
,
f
d,e,f
d,e,f对应的分享值如下:

令
[
χ
]
1
=
[
λ
f
]
1
,
[
χ
]
2
=
[
λ
f
]
2
→
[
χ
]
=
[
λ
f
]
1
+
[
λ
f
]
2
[\chi]_1=[\lambda_f]_1, [\chi]_2=[\lambda_f]_2\quad\rightarrow\quad [\chi]=[\lambda_f]_1+[\lambda_f]_2
[χ]1=[λf]1,[χ]2=[λf]2→[χ]=[λf]1+[λf]2
令
γ
x
γ
y
+
ψ
=
f
+
λ
f
→
ψ
=
f
+
λ
f
−
γ
x
γ
y
\gamma_x\gamma_y+\psi=f+\lambda_f\quad\rightarrow\quad \psi=f+\lambda_f-\gamma_x\gamma_y
γxγy+ψ=f+λf→ψ=f+λf−γxγy
令
[
Γ
x
y
]
j
=
γ
x
[
α
y
]
j
+
γ
y
[
α
x
]
j
+
[
ψ
]
j
−
[
χ
]
j
j
∈
{
1
,
2
}
[\Gamma_{xy}]_j=\gamma_x[\alpha_y]_j+\gamma_y[\alpha_x]_j+[\psi]_j-[\chi]_j \quad j\in\{1,2\}
[Γxy]j=γx[αy]j+γy[αx]j+[ψ]j−[χ]jj∈{1,2} ,其中
[
ψ
]
1
=
r
,
[
ψ
]
2
=
ψ
−
r
[\psi]_1=r, [\psi]_2=\psi-r
[ψ]1=r,[ψ]2=ψ−r ,
r
∈
Z
2
l
r\in\mathbb{Z}_2^l
r∈Z2l是一个随机值.
我们可以得到:
Γ
x
y
=
γ
x
α
y
+
γ
y
α
x
+
ψ
−
χ
=
(
d
+
λ
d
)
λ
e
+
(
e
+
λ
e
)
λ
d
+
(
f
+
λ
f
−
γ
x
γ
y
)
−
λ
f
=
(
d
+
λ
d
)
(
e
+
λ
e
)
−
d
e
+
λ
d
λ
e
+
(
f
−
γ
x
γ
y
)
=
γ
x
γ
y
−
f
+
λ
d
λ
e
+
(
f
−
γ
x
γ
y
)
=
λ
d
λ
e
=
α
x
α
y
\begin{aligned} \Gamma_{xy}&=\gamma_x\alpha_y+\gamma_y\alpha_x+\psi-\chi \\ &=(d+\lambda_d)\lambda_e+(e+\lambda_e)\lambda_d+(f+\lambda_f-\gamma_x\gamma_y)-\lambda_f \\ &=(d+\lambda_d)(e+\lambda_e)-de+\lambda_d\lambda_e+(f-\gamma_x\gamma_y)\\ &=\gamma_x\gamma_y-f+\lambda_d\lambda_e+(f-\gamma_x\gamma_y)\\ &=\lambda_d\lambda_e\\ &=\alpha_x\alpha_y \end{aligned}
Γxy=γxαy+γyαx+ψ−χ=(d+λd)λe+(e+λe)λd+(f+λf−γxγy)−λf=(d+λd)(e+λe)−de+λdλe+(f−γxγy)=γxγy−f+λdλe+(f−γxγy)=λdλe=αxαy
这说明我们构造的三元组是有效的。
- 问题二:我们再利用
β
+
γ
\beta+\gamma
β+γ

令
β
x
∗
=
β
x
+
γ
x
,
β
y
∗
=
β
y
+
γ
y
\beta_x^*=\beta_x+\gamma_x, \beta_y^*=\beta_y+\gamma_y
βx∗=βx+γx,βy∗=βy+γy,
P
0
P_0
P0 计算
β
z
∗
=
−
β
x
∗
α
y
−
β
y
∗
α
x
+
2
Γ
x
y
+
α
z
\beta_z^*=-\beta_x^*\alpha_y-\beta_y^*\alpha_x+2\Gamma_{xy}+\alpha_z
βz∗=−βx∗αy−βy∗αx+2Γxy+αz.
通过推导可以得到:
β
z
∗
=
−
β
x
∗
α
y
−
β
y
∗
α
x
+
2
Γ
x
y
+
α
z
=
−
(
β
x
+
γ
x
)
α
y
−
(
β
y
+
γ
y
)
α
x
+
2
Γ
x
y
+
α
z
=
(
−
β
x
α
y
−
β
y
α
x
+
Γ
x
y
+
α
z
)
−
(
γ
x
α
y
+
γ
y
α
x
−
Γ
x
y
)
=
(
β
z
−
β
x
β
y
)
−
(
γ
x
α
y
+
γ
y
α
x
−
Γ
x
y
+
ψ
)
+
ψ
=
(
β
z
−
β
x
β
y
+
ψ
)
−
χ
\begin{aligned} \beta_z^*&=-\beta_x^*\alpha_y-\beta_y^*\alpha_x+2\Gamma_{xy}+\alpha_z\\ &=-(\beta_x+\gamma_x)\alpha_y-(\beta_y+\gamma_y)\alpha_x+2\Gamma_{xy}+\alpha_z\\ &=(-\beta_x\alpha_y-\beta_y\alpha_x+\Gamma_{xy}+\alpha_z)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy})\\ &=(\beta_z-\beta_x\beta_y)-(\gamma_x\alpha_y+\gamma_y\alpha_x-\Gamma_{xy}+\psi)+\psi\\ &=(\beta_z-\beta_x\beta_y+\psi)-\chi \end{aligned}
βz∗=−βx∗αy−βy∗αx+2Γxy+αz=−(βx+γx)αy−(βy+γy)αx+2Γxy+αz=(−βxαy−βyαx+Γxy+αz)−(γxαy+γyαx−Γxy)=(βz−βxβy)−(γxαy+γyαx−Γxy+ψ)+ψ=(βz−βxβy+ψ)−χ
因此,让
P
0
P_0
P0 发送
β
z
∗
+
χ
\beta_z^*+\chi
βz∗+χ 给
P
1
P_1
P1 和
P
2
P_2
P2 ,
P
1
P_1
P1 和
P
2
P_2
P2计算
β
z
−
β
x
β
y
+
ψ
\beta_z-\beta_x\beta_y+\psi
βz−βxβy+ψ并与收到的来自
P
0
P_0
P0的
β
z
∗
+
χ
\beta_z^*+\chi
βz∗+χ比较, 只有当二者一致时,才能证明
β
z
\beta_z
βz的正确性.
- 问题三:解决方案比较简单,为了验证 P 1 P_1 P1发送的 β z + γ z \beta_z+\gamma_z βz+γz的正确性,让 P 2 P_2 P2同时发送其哈希值 H ( β z + γ z ) H(\beta_z+\gamma_z) H(βz+γz)给 P 0 P_0 P0, 当 P 0 P_0 P0收到的二者不一致时就中止.
至此,所有问题都解决,完整的乘法协议如下:

























 1926
1926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








