HDU 5751 Eades（单调栈+FFT）

Description
Peter有一个序列a[1],a[2],…,a[n]，定义g(l,r)表示子序列{a[l],a[l+1],…,a[r]}的最大值, f(l,r)=sum{[a[i]==g(l,r)]}(l<=i<=r).
注意[condition]=1当且仅当condition是true, 否则[condition]=0
对于每个整数k∈{1,2,…,n}, Peter想要知道有多少整数对l和r (l≤r)满足f(l,r)=k
Input
输入包含多组数据, 第一行包含一个整数T表示测试数据组数. 对于每组数据:
第一行包含一个整数n(1≤n≤60000)表示序列的长度，第二行包含n个整数ai(1≤ai≤n)
Output
对于每组数据, 输出一个整数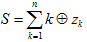 ，其中z​[k]表示满足f(l,r)=k的数对l和r的个数, ⊕是异或位运算操作.
Sample Input
3
3
1 2 3
4
1 1 1 1
6
1 2 2 1 1 2
Sample Output
12
12
36
Solution
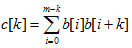
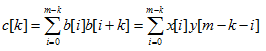
首先用单调栈预处理出每个数x作为最大值的最大区间[lx,rx]，假设在这个区间中x出现m次，出现位置分别为p[1],p[2],…,p[m]，那么这m个x就可以转化为一个长度为m+1的序列b，b[0]=p[1]-lx+1，b[m]=rx-p[m]+1，b[i]=p[i+1]-p[i]，i=1,2,…,m-1，简单推导可知这m个x对z[k]的贡献为，令x[i]=b[i],y[i]=b[m-i]，那么有，后者直接计算复杂度为O(m^2)，用fft对x[0],…,x[m]和y[0],…,y[m]做一遍卷积可以将复杂度降为O(mlogm)，注意此处计算的是m个x对答案的贡献
Code

#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
namespace fastIO 
{
    #define BUF_SIZE 100000
    //fread -> read
    bool IOerror=0;
    inline char nc() 
    {
        static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE;
        if(p1==pend) 
        {
            p1=buf;
            pend=buf+fread(buf,1,BUF_SIZE,stdin);
            if(pend==p1) 
            {
                IOerror=1;
                return -1;
            }
        }
        return *p1++;
    }
    inline bool blank(char ch) 
    {
        return ch==' '||ch=='\n'||ch=='\r'||ch=='\t';
    }
    inline void read(int &x) 
    {
        char ch;
        while(blank(ch=nc()));
        if(IOerror)return;
        for(x=ch-'0';(ch=nc())>='0'&&ch<='9';x=x*10+ch-'0');
    }
        inline void readc(char &x)
    {
        char ch;
        while(blank(ch=nc()));
        if(IOerror)return;
        x=ch;
    }
    #undef BUF_SIZE
};
using namespace fastIO;
typedef long long ll;
#define maxn 65536+5
const double pi=acos(-1.0);
int T,n,a[maxn],l[maxn],r[maxn],flag[maxn],b[maxn],c[maxn];
vector<int>v[maxn];
ll d[maxn<<1],ans[maxn<<1],sum;
struct cp 
{
    double a,b;
    cp operator +(const cp &o)const {return (cp){a+o.a,b+o.b};}
    cp operator -(const cp &o)const {return (cp){a-o.a,b-o.b};}
    cp operator *(const cp &o)const {return (cp){a*o.a-b*o.b,b*o.a+a*o.b};}
    cp operator *(const double &o)const {return (cp){a*o,b*o};}
    cp operator !() const{return (cp){a,-b};}
}w[maxn];
int pos[maxn];
void fft_init(int len)
{
    int j=0;
    while((1<<j)<len)j++;
    j--;
    for(int i=0;i<len;i++)
        pos[i]=pos[i>>1]>>1|((i&1)<<j);
}
void fft(cp *x,int len,int sta)
{
    for(int i=0;i<len;i++)
        if(i<pos[i])swap(x[i],x[pos[i]]);
    w[0]=(cp){1,0};
    for(unsigned i=2;i<=len;i<<=1)
    {
        cp g=(cp){cos(2*pi/i),sin(2*pi/i)*sta};
        for(int j=i>>1;j>=0;j-=2)w[j]=w[j>>1];
        for(int j=1;j<i>>1;j+=2)w[j]=w[j-1]*g;
        for(int j=0;j<len;j+=i)
        {
            cp *a=x+j,*b=a+(i>>1);
            for(int l=0;l<i>>1;l++)
            {
                cp o=b[l]*w[l];
                b[l]=a[l]-o;
                a[l]=a[l]+o;
            }
        }
    }
    if(sta==-1)for(int i=0;i<len;i++)x[i].a/=len,x[i].b/=len;
}

//1.5次DFT 
cp x[maxn],y[maxn],z[maxn];
void FFT(int *a,int *b,int n,int m,ll *c)
{
    int len=1;
    while(len<=(n+m)>>1)len<<=1;
    fft_init(len);
    for(int i=n/2;i<len;i++)x[i].a=x[i].b=0;
    for(int i=m/2;i<len;i++)y[i].a=y[i].b=0;
    for(int i=0;i<n;i++)(i&1?x[i>>1].b:x[i>>1].a)=a[i];
    for(int i=0;i<m;i++)(i&1?y[i>>1].b:y[i>>1].a)=b[i];
    fft(x,len,1),fft(y,len,1);
    for(int i=0;i<len/2;i++)
    {
        int j=len-1&len-i;
        z[i]=x[i]*y[i]-(x[i]-!x[j])*(y[i]-!y[j])*(w[i]+(cp){1,0})*0.25;
    }
    for(int i=len/2;i<len;i++)
    {
        int j=len-1&len-i;
        z[i]=x[i]*y[i]-(x[i]-!x[j])*(y[i]-!y[j])*((cp){1,0}-w[i^len>>1])*0.25;
    }
    fft(z,len,-1);
    for(int i=0;i<n+m;i++)
        if(i&1)c[i]=(ll)(z[i>>1].b+0.5);
        else c[i]=(ll)(z[i>>1].a+0.5);
}
void init()
{
    sum=0;
    memset(ans,0,sizeof(ans));
    memset(flag,0,sizeof(flag));
    for(int i=1;i<=n;i++)v[i].clear();
}
void deal(int *a,int n)
{
    int p,sta[maxn];
    p=0;
    for(int i=1;i<=n;i++)
    {
        if(!p||a[i]<=a[sta[p]])sta[++p]=i;
        else 
        {
            while(p&&a[i]>a[sta[p]])
                r[sta[p]]=i-1,p--;
            sta[++p]=i;
        }
    }
    while(p)r[sta[p]]=n,p--;
    for(int i=n;i>=1;i--)
    {
        if(!p||a[i]<=a[sta[p]])sta[++p]=i;
        else 
        {
            while(p&&a[i]>a[sta[p]])
                l[sta[p]]=i+1,p--;
            sta[++p]=i;
        }
    }
    while(p)l[sta[p]]=1,p--;
}
void FFT(int *b,int m)
{
    int len=1;
    while(len<m)len<<=1;
    fft_init(len);
    for(int i=m/2;i<len;i++)x[i].a=x[i].b=0;
    for(int i=m/2;i<len;i++)y[i].a=y[i].b=0;
    for(int i=0;i<m;i++)(i&1?x[i>>1].b:x[i>>1].a)=b[i];
    for(int i=0;i<m;i++)(i&1?y[i>>1].b:y[i>>1].a)=b[m-1-i];
    fft(x,len,1),fft(y,len,1);
    for(int i=0;i<len/2;i++)
    {
        int j=len-1&len-i;
        z[i]=x[i]*y[i]-(x[i]-!x[j])*(y[i]-!y[j])*(w[i]+(cp){1,0})*0.25;
    }
    for(int i=len/2;i<len;i++)
    {
        int j=len-1&len-i;
        z[i]=x[i]*y[i]-(x[i]-!x[j])*(y[i]-!y[j])*((cp){1,0}-w[i^len>>1])*0.25;
    }
    fft(z,len,-1);
    for(int i=0;i<m;i++)
        if(i&1)ans[m-1-i]+=(ll)(z[i>>1].b+0.5);
        else ans[m-1-i]+=(ll)(z[i>>1].a+0.5);
}
int main()
{
    read(T);
    while(T--)
    {
        init();
        read(n);
        for(int i=1;i<=n;i++)
            read(a[i]),v[a[i]].push_back(i);
        deal(a,n);
        for(int i=1;i<=n;i++)
            if(!flag[i])
            {
                int m=0,last=l[i]-1,j;
                for(j=0;j<v[a[i]].size();j++)
                {
                    if(v[a[i]][j]>r[i])break;
                    int now=v[a[i]][j];
                    flag[now]=1;
                    b[m++]=now-last;
                    last=now;
                }
                while(v[a[i]].size()&&v[a[i]][0]<=r[i])
                    v[a[i]].erase(v[a[i]].begin());
                b[m++]=r[i]-last+1;
                FFT(b,m);
            }
        for(int i=1;i<=n;i++)sum+=i^ans[i];
        printf("%I64d\n",sum);
    }
    return 0;
}