数据结构（c++）学习笔记--图

VaIOReTto1

已于 2023-01-28 17:29:05 修改

阅读量369

点赞数 1

分类专栏：数据结构（c++）学习笔记文章标签： c++ 数据结构学习

于 2023-01-27 00:51:27 首次发布

本文链接：https://blog.csdn.net/VaIOReTto1/article/details/128768756

版权

数据结构（c++）学习笔记专栏收录该内容

13 篇文章 3 订阅

订阅专栏

一、概述

1.基本术语

G = (V; E)
- vertex: n = |V|
- edge|arc: e = |E|

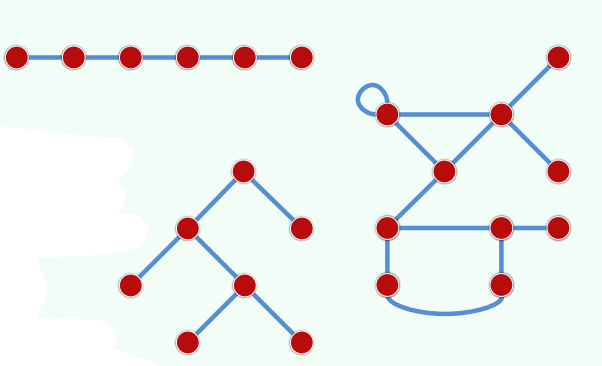
- 同一条边的两个顶点，彼此邻接（adjacency）
- 同一顶点自我邻接，构成自环（self-loop）
- 不含自环及重边，即为简单图（simple graph）
- 非简单（non-simple）图，暂不讨论
顶点与其所属的边，彼此关联（incidence）
度（degree/valency）：与同一顶点关联的边数

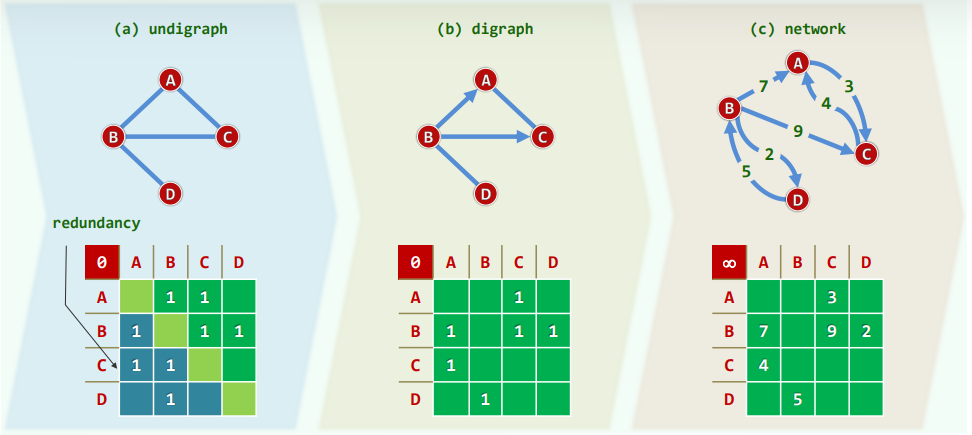
2.无向图 + 有向图

若邻接顶点u和v的次序无所谓则(u, v)为无向边（undirected edge）
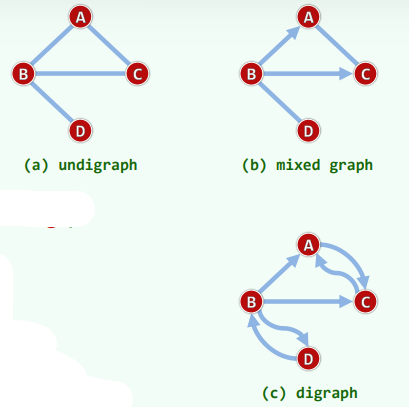
所有边均无方向的图，即无向图（undigraph）
反之，有向图（digraph）中均为有向边（directed edge） u、v分别称作边(u, v)的尾（tail）、头（head）
无向边、有向边并存的图，称作混合图（mixed graph）

3.路径 + 环路

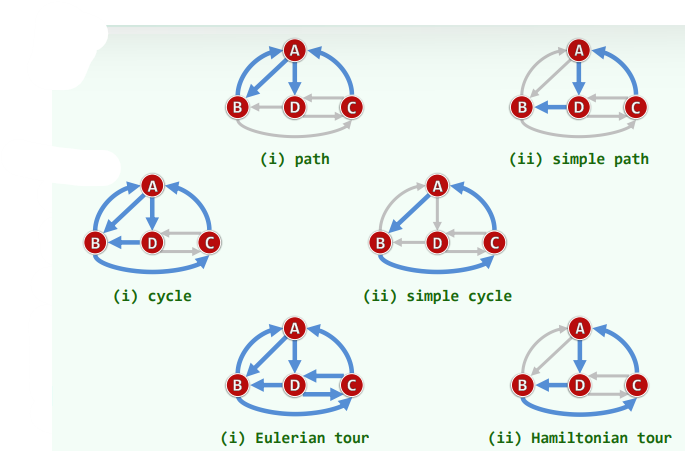
路径$π=<v_0,v_1,…,v_k> ，长度|π| = k $
简单路径： $v_i ≠ v_j$ 除非 i = j
环/环路： $v_0 = v_k$
有向无环图（DAG）
欧拉环路：$|π| = |E| $,各边恰好出现一次
哈密尔顿环路：$|π| = |V| $,各顶点恰好出现一次

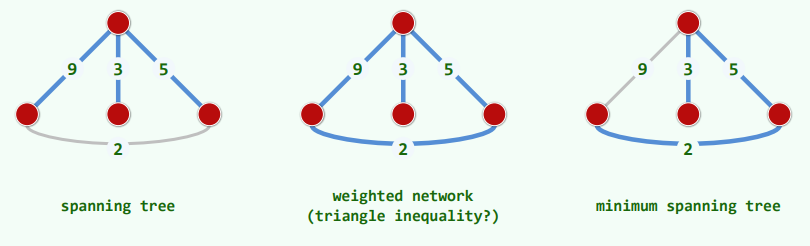
4.支撑树 + 带权网络 + 最小支撑树

图G = (V; E)的子图T = (V; F)若是树，即为其支撑树（spanning tree）同一图的支撑树，通常并不唯一
各边e均有对应的权值wt(e)，则为带权网络（weighted network）
同一网络的支撑树中，总权重最小者为最小支撑树（MST）

二、邻接矩阵

1.构思

1.1 Graph 模板类

template<typename Tv,typename Te> class Graph { 
private: 
    void reset() { //所有顶点、边的辅助信息复位 
        for ( Rank v = 0; v < n; v++ ) { //顶点 
            status(v) = UNDISCOVERED; 
            dTime(v) = fTime(v) = -1; 
            parent(v) = -1; 
            priority(v) = INT_MAX; 
            for ( Rank u = 0; u < n; u++ ) //边 
                if ( exists(v, u) ) type(v, u) = UNDETERMINED; 
        } 
    } 
public: 
    int n, e; //顶点、边数目 
    /* ... 顶点操作、边操作、图算法：无论如何实现，接口必须统一 ... */ 
}

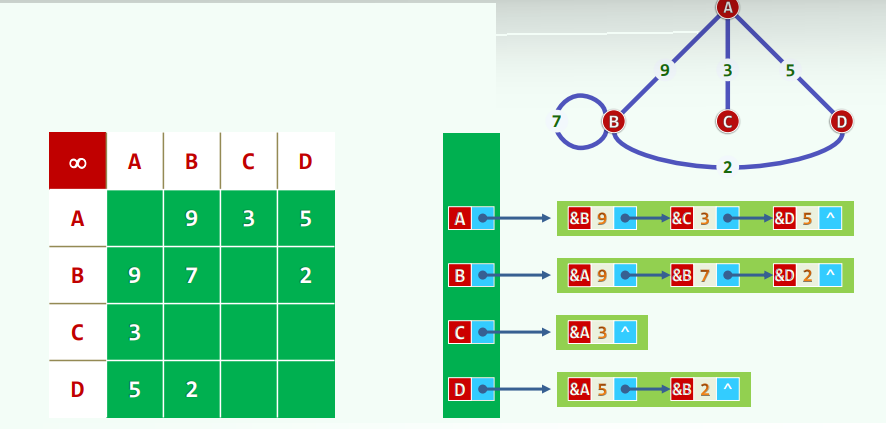
1.2 邻接矩阵 + 关联矩阵

邻接矩阵(adjacency matrix)：记录顶点之间的邻接关系
- 一一对应：矩阵元素 ⇔ 图中可能存在的边
- A(v, u) = 1 （若顶点v与u之间存在一条边）/= 0 （否则）
- 既然只考察简单图，对角线统一设置为0
- 空间复杂度为(n2)，与图中实际的边数无关

关联矩阵(incidence matrix)：记录顶点与边之间的关联关系
- 空间复杂度为 $Θ(n*e) = O(n^3)$
- 空间利用率 = 2e/ne = 2/n
- 解决某些问题时十分有效

1.3 实例

2.模板实现

//Vertex
using VStatus = enum { UNDISCOVERED, DISCOVERED, VISITED }; 
template<typename Tv> struct Vertex { //不再严格封装 
    Tv data; int inDegree, outDegree; 
    VStatus status; //（如上三种）状态 
    int dTime, fTime; //时间标签 
    Rank parent; //在遍历树中的父节点 
    int priority; //在遍历树中的优先级（最短通路、极短跨边等） 
    Vertex( Tv const & d ) : //构造新顶点 
        data( d ), inDegree( 0 ), outDegree( 0 ), status( UNDISCOVERED ), 
        dTime( -1 ), fTime( -1 ), parent( -1 ), priority( INT_MAX ) {} 
}

//Edge
using EType = enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD }; 
template<typename Te> struct Edge { //不再严格封装 
    Te data; //数据
    int weight; //权重 
    EType type; //在遍历树中所属的类型 
    Edge( Te const & d, int w ) : //构造新边 
        data(d), weight(w), type(UNDETERMINED) {} 
};

//GraphMatrix
template<typename Tv,typename Te> class GraphMatrix : public Graph { 
private: 
    Vector< Vertex > V; //顶点集 
    Vector< Vector< Edge* > > E; //边集 
public: // 操作接口：顶点相关、边相关、... 
    GraphMatrix() { n = e = 0; } 
    ~GraphMatrix() { 
    for ( Rank v = 0; v < n; v++ ) 
        for ( Rank u = 0; u < n; u++ ) 
            delete E[v][u]; //清除所有边记录 
    } 
}

3.静态操作

3.1 顶点的读写

Tv & vertex(Rank v) { return V[v].data; } //数据 
int inDegree(Rank v) { return V[v].inDegree; } //入度 
int outDegree(Rank v) { return V[v].outDegree; } //出度 
VStatus & status(Rank v) { return V[v].status; } //状态 
int & dTime(Rank v) { return V[v].dTime; } //时间标签dTime 
int & fTime(Rank v) { return V[v].fTime; } //时间标签fTime 
Rank & parent(Rank v) { return V[v].parent; } //在遍历树中的父亲 
int & priority(Rank v) { return V[v].priority; } //优先级数

3.2 边的读写

bool exists( Rank v, Rank u ) { //判断边(v, u)是否存在（短路求值） 
    return (v < n) && (u < n) && E[v][u] != NULL; 
} //以下假定exists(v, u) = true 

Te & edge( Rank v, Rank u ) { return E[v][u]->data; } //数值 
EType & type( Rank v, Rank u ) { return E[v][u]->type; } //类型 
int & weight( Rank v, Rank u ) { return E[v][u]->weight; } //权重

3.3 邻点的枚举

Rank firstNbr( Rank v ) { return nextNbr( v, n ); } //假想哨兵 

Rank nextNbr( Rank v, Rank u ) { //若已枚举至邻居u，则转向下一邻居 
    while ( -1 < u ) && ! exists( v, --u ) ); //逆向顺序查找 
    return u; 
} //O(n)——改用邻接表，可提高至O(1 + outDegree(v))

4.动态操作

4.1 边的插入

void insert( Te const & edge, int w, Rank v, Rank u ) { 
    if ( exists(v, u) ) return; //忽略已有的边 
    E[v][u] = new Edge( edge, w ); //创建新边（权重为w） 
    e++; //更新边计数 
    V[v].outDegree++; //更新顶点v的出度 
    V[u].inDegree++; //更新顶点u的入度
}

4.2 边的删除

Te remove( Rank v, Rank u ) { //删除（已确认存在的）边(v, u) 
    Te eBak = edge(v, u); //备份边(v, u)的信息 
    delete E[v][u]; E[v][u] = NULL; //删除边(v, u) 
    e--; //更新边计数 
    V[v].outDegree--; //更新顶点v的出度 
    V[u].inDegree--; //更新顶点u的入度 
    return eBak; //返回被删除边的信息
}

4.3 顶点插入

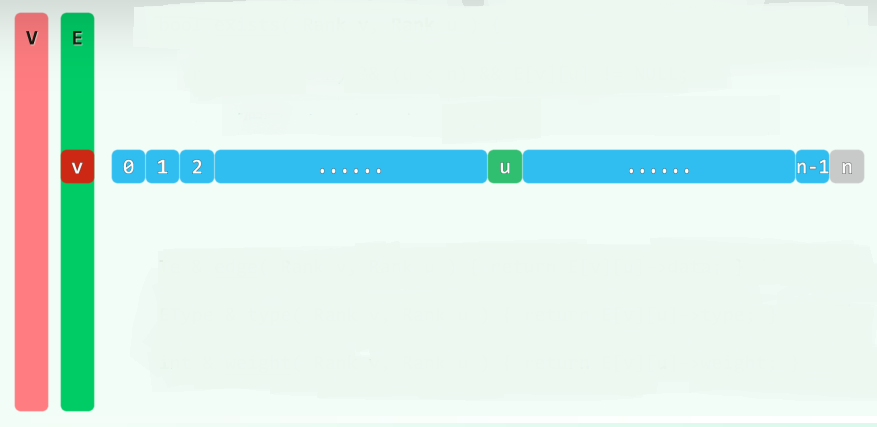
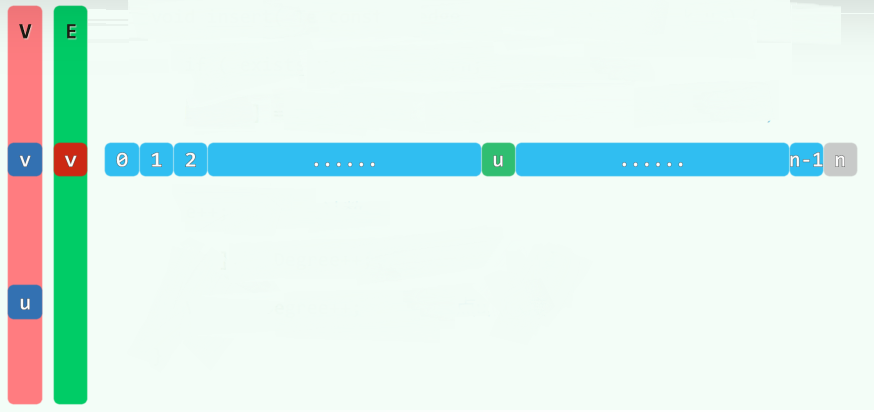
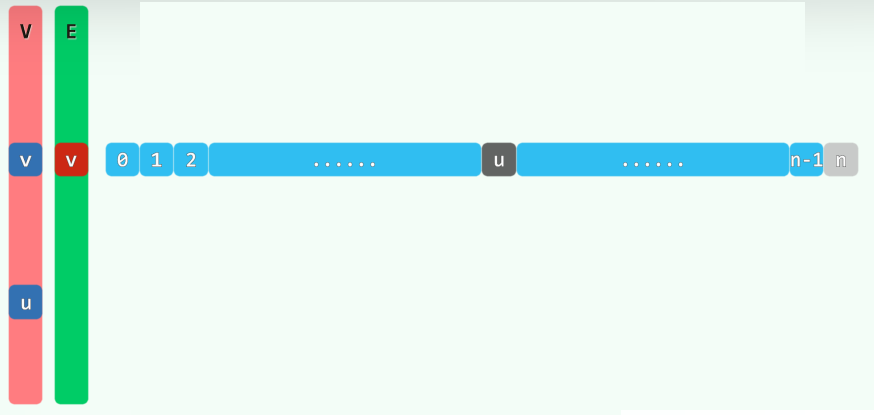
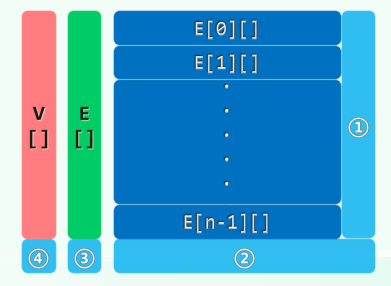
Rank insert( Tv const & vertex ) { //插入顶点，返回编号 
    for ( Rank u = 0; u < n; u++ ) E[u].insert( NULL ); n++; //① 
    E.insert( Vector< Edge* >( n, n, NULL ) ); //②③ 
    return V.insert( Vertex( vertex ) ); //④
}

4.4 顶点删除

Tv remove( Rank v ) { //删除顶点及其关联边，返回该顶点信息 
    for ( Rank u = 0; u < n; u++ ) //删除所有出边 
        if ( exists( v, u ) ) { delete E[v][u]; V[u].inDegree--; e-- } 
    E.remove(v); n--; //删除第v行 
    Tv vBak = vertex( v ); V.remove( v ); //备份之后，删除顶点v 
    for ( Rank u = 0; u < n; u++ ) //删除所有入边及第v列 
        if ( Edge * x = E[u].remove( v ) ) { delete x; V[u].outDegree--; e--; } 
    return vBak; //返回被删除顶点的信息
}

5.性能分析

5.1 优点

直观，易于理解和实现
适用范围广泛尤其适用于稠密图（dense graph）
判断两点之间是否存在联边：O(1)
获取顶点的（出/入）度数：O(1)
添加、删除边后更新度数：O(1)
扩展性（scalability）：得益于Vector良好的控制策略，空间溢出等情况可被“透明地”处理

5.2 缺点

$Θ(n^2)$ 空间，与边数无关！
平面图（planar graph）：可嵌入于平面的图
欧拉公式（Euler’s formula）： v - e + f - c = 1, for any PG
平面图：e ≤ 3n - 6 = O(n) << $n^2$ ，此时空间利用率 ≈ 1/n
稀疏图（sparse graph）：空间利用率同样很低，可采用压缩存储技术

三、邻接表

1.邻接表

如何避免邻接矩阵的空间浪费？
将邻接矩阵的各行组织为列表，只记录存在的边，等效于，每一顶点v对应于列表： $L_v=$ {u | <v,u> ∈E }

2.复杂度

2.1 空间复杂度

有向图 = O(n + e）
无向图 = O(n + 2e) = O(n + e)
- 注意：无向弧被重复存储
适用于稀疏图
平面图 = O(n + 3n) = O(n) 较之邻接矩阵，有极大改

2.2 时间复杂度

建立邻接表（递增式构造）：O( n + e )
枚举所有以顶点v为尾的弧：O( 1 + deg(v) ) //遍历v的邻接表
枚举（无向图中）顶点v的邻居：O( 1 + deg(v) ) //遍历v的邻接表
枚举所有以顶点v为头的弧：O( n + e ) //遍历所有邻接表
- 可改进至O( 1 + deg(v) ) //建立逆邻接表
计算顶点v的出度/入度：
- 增加度数记录域：O( n )附加空间
- 增加/删除弧时更新度数：O( 1 )时间 //总体O(e)时间
- 每次查询：O(1)时间！

3.取舍原则

	邻接矩阵	邻接表
适用场合	经常检测边的存在，经常做边的插入/删除，图的规模固定，稠密图	经常计算顶点的度数，顶点数目不确定，经常做遍历，稀疏图

四、广度优先算法

1.算法

始自顶点s的广度优先搜索 
    访问顶点s 
    依次访问s所有尚未访问的邻接顶点 
    依次访问它们尚未访问的邻接顶点 
    ... 
    如此反复 
    直至没有尚未访问的邻接顶点

以上策略及过程完全等同于树的层次遍历，事实上，BFS也的确会构造出原图的一棵支撑树（BFS tree）

template<typename Tv,typename Te> 
void Graph::BFS( Rank v, int & clock ) { 
    Queue Q; status(v) = DISCOVERED; Q.enqueue(v); //初始化 
    while ( ! Q.empty() ) { 
        Rank v = Q.dequeue(); dTime(v) = ++clock; //取出队首顶点v，并 
        for ( Rank u = firstNbr(v); -1 < u; u = nextNbr(v, u) ) //考查每一邻居u
            if ( UNDISCOVERED == status(u) ) { //若u尚未被发现，则 
                status(u) = DISCOVERED; Q.enqueue(u); //发现该顶点 
                type(v, u) = TREE; parent(u) = v; //引入树边 
            } else //若u已被发现（正在队列中），或者甚至已访问完毕（已出队列），则 
                type(v, u) = CROSS; //将(v, u)归类于跨边
        tatus(v) = VISITED; //至此，当前顶点访问完毕 
    } 
}

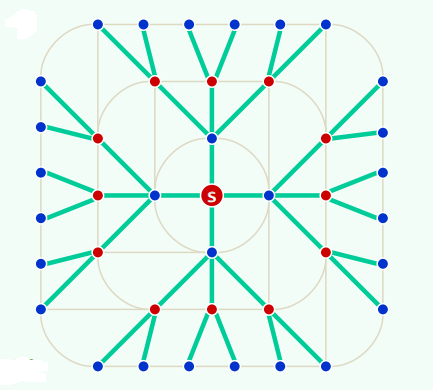
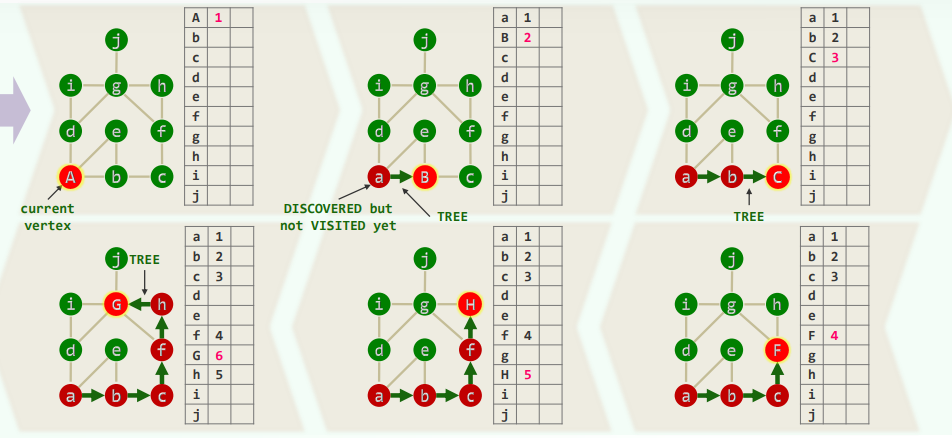
2.实例

3.推广

3.1 连通分量 + 可达分量

问题
- 给定无向图，找出其中任一顶点s所在的连通图
- 给定有向图，找出源自其中任一顶点s的可达分量
算法
- 从s出发做BFS
- 输出所有被发现的顶点
- 队列为空后立即终止，无需考虑其它顶点

3.2 Graph::bfs()

template<typename Tv,typename Te> 
void Graph::bfs( Rank s ) { //s为起始顶点 
    reset(); int clock = 0; Rank v = s; //初始化Θ(n+e) 
    do //逐一检查所有顶点，一旦遇到尚未发现的顶点 
        if ( UNDISCOVERED == status(v) ) //累计Θ(n) 
            BFS( v, clock ); //即从该顶点出发启动一次BFS 
    while ( s != ( v = ( ( v+1 ) % n ) ) ); //按序号访问，不漏不重 
} //无论共有多少连通/可达分量...

3.3 复杂度

bfs()的初始化（reset()）：O(n+e)
BFS()的迭代
- 外循环（while ( !Q.empty() )）,每个顶点各进入1次
- 内循环（枚举v的每一邻居）： O(1+deg(v))（改用邻接表）
- 总共： $O(\sum_{v∈V}(1+deg(v)))=O(n+2e)$
整个算法：O(n+e)+O(n+2e)=O(n+e)

4.性质及规律

4.1 边分类

经BFS后，所有边将确定方向，且被分为两类
(v,u)被标记为TREE时，v为DISCOVERED且u为UNDISCOVERED

(v,u)被标记为CROSS时，v和u均为DISCOVERED 或者 v为DISCOVERED而u为VISITED

不论(v,u)是有向边或无向边，两种情况均可能出现

4.2 BFS树/森林

对于（起始于v的）每一连通/可达分量，bfs()进入BFS(v)恰好1次
进入BFS(v)时，队列为空；v所属分量内的每个顶点
- 迟早会以UNDISCOVERED状态进队1次
- 进队后随即转为DISCOVERED状态，并生成一条树边
- 迟早会出队并转为VISITED状态
- 退出BFS(v)时，队列为空
BFS(v)以v为根，生成一棵BFS树
bfs()生成一个BFS森林包含 c 棵树、n-c 条树边和 e-n+c 条跨边

4.3 最短路径

无向图中，顶点v到u的（最近）距离记作dist(v, u)
BFS过程中，队列Q犹如一条贪吃蛇
- 其中的顶点按dist(s)单调排列
- 相邻顶点的dist(s)相差不超过1
- 首、末顶点的dist(s)相差不超过1
- 由树边联接的顶点，dist(s)恰好相差1
- 由跨边联接的顶点，dist(s)至多相差1
BFS树中从s到v的路径，即是二者在原图中的最短通路

五、深度优先搜索

1.算法

 DFS(s) //始自顶点s的深度优先搜索
     访问顶点s
     若s尚有未被访问的邻居，则 任取其一u，递归执行DFS(u)
     否则，返回 
 若此时尚有顶点未被访问，任取这样的一个顶点作起始点

重复上述过程，直至所有顶点都被访问到
对树而言，等效于先序遍历：DFS也的确会构造出原图的一棵支撑树（DFS tree）

template<typename Tv,typename Te>  
void Graph::DFS( Rank v, int & clock ) { 
    dTime(v) = ++clock; status(v) = DISCOVERED; //发现当前顶点v 
    for ( Rank u = firstNbr(v); -1 < u; u = nextNbr(v, u) ) //考察v的每一邻居u 
        switch ( status(u) ) { //并视其状态分别处理 
            case UNDISCOVERED: //u尚未发现，意味着支撑树可在此拓展 
                type(v, u) = TREE; parent(u) = v; DFS( u, clock ); break; //递归 
            case DISCOVERED: //u已被发现但尚未访问完毕，应属被后代指向的祖先 
                type(v, u) = BACKWARD; break; 
            default: //u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边 
                type(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break; 
        }
    status(v) = VISITED; fTime(v) = ++clock; //至此，当前顶点v方告访问完毕
}

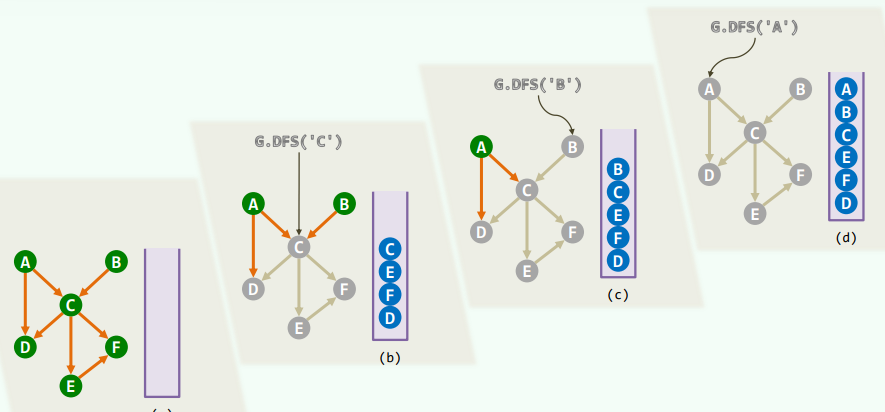
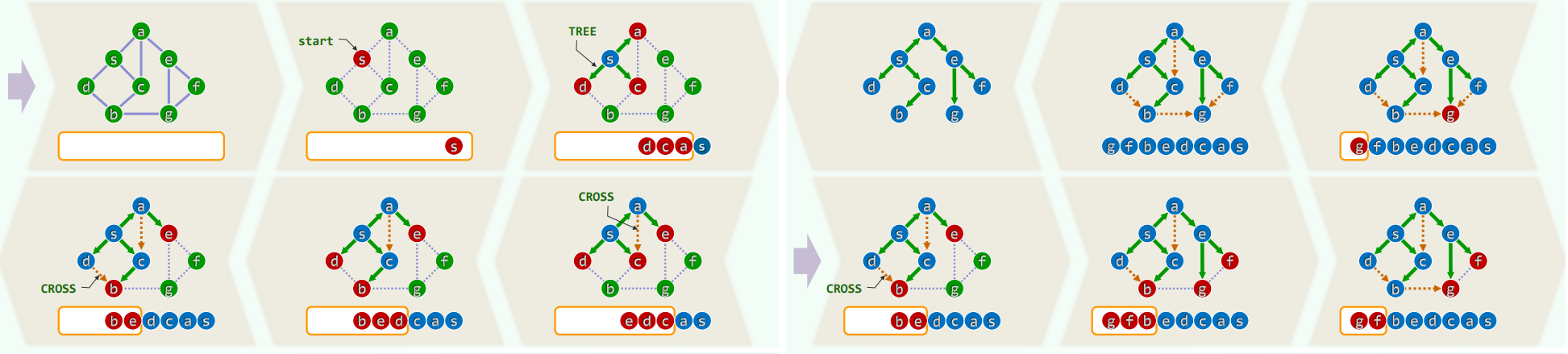
2.实例（无向图）

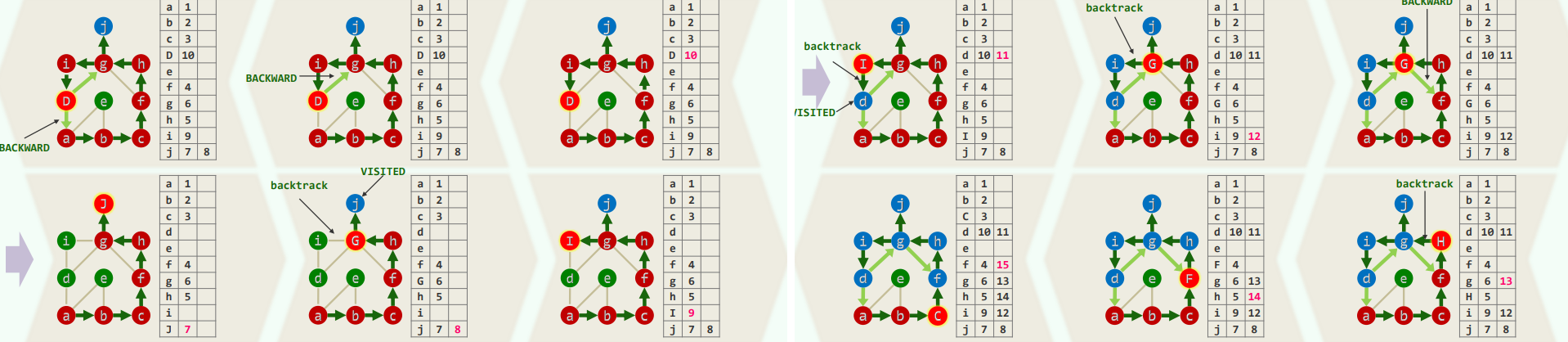
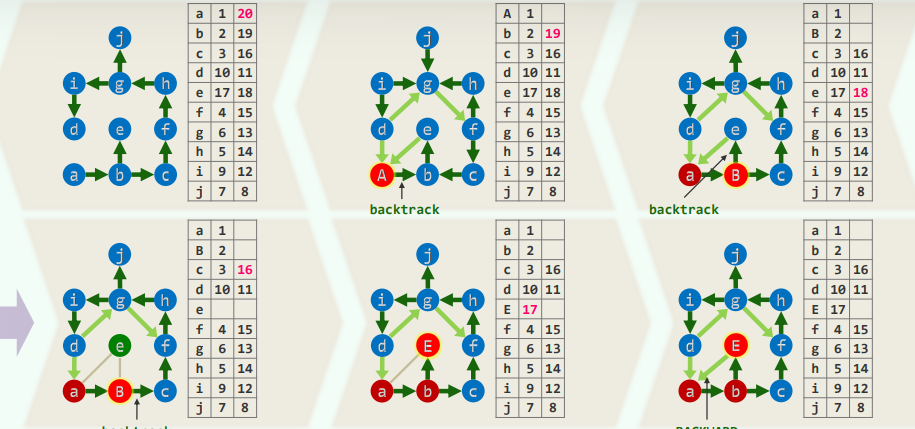
3.推广

与BFS(v)类似，DFS(v)也可遍历v所属分量
与bfs(s)类似（采用邻接表），dfs(s)也可在累计O(n+e)时间内
- 对于每一连通/可达分量，从其起始顶点v进入DFS(v)恰好1次，并最终生成一个DFS森林（包含 c 棵树、n-c 条树边）

template<typename Tv,typename Te> 
void Graph::dfs( Rank s ) { //s为起始顶点 
    reset(); int clock = 0; Rank v = s; //初始化 
    do //逐一检查所有顶点，一旦遇到尚未发现的顶点v 
        if ( UNDISCOVERED == status(v) ) 
            DFS( v, clock ); //即从v出发启动一次DFS 
    while ( s != ( v = ( ( v+1 ) % n ) ) ); //按序号访问，不漏不重 
}

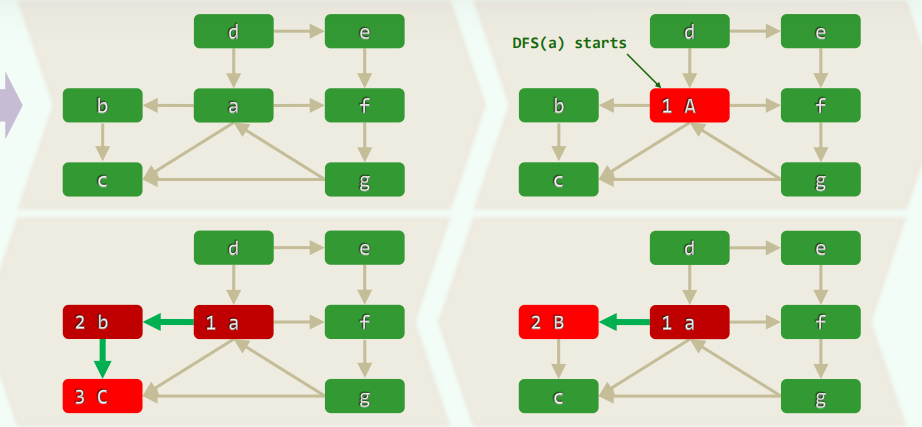
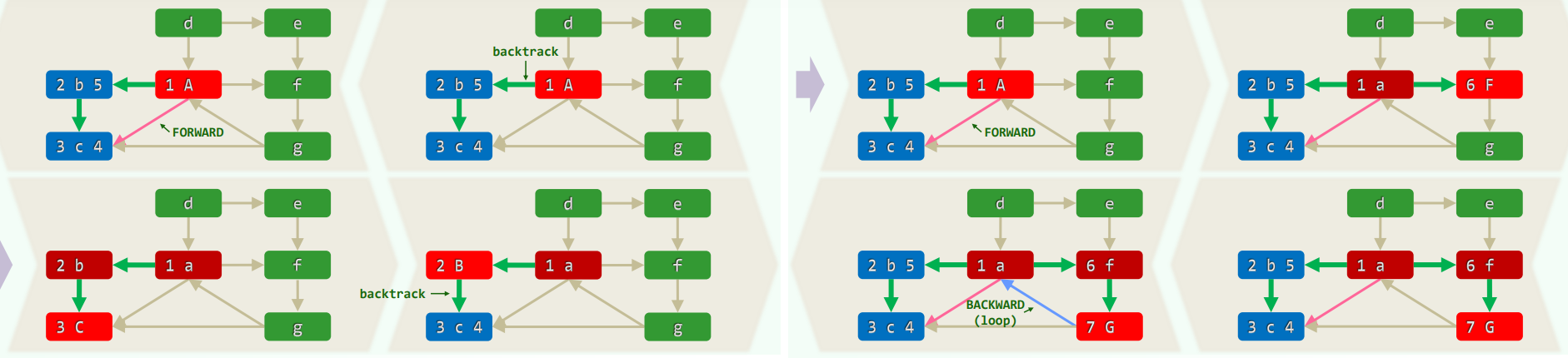
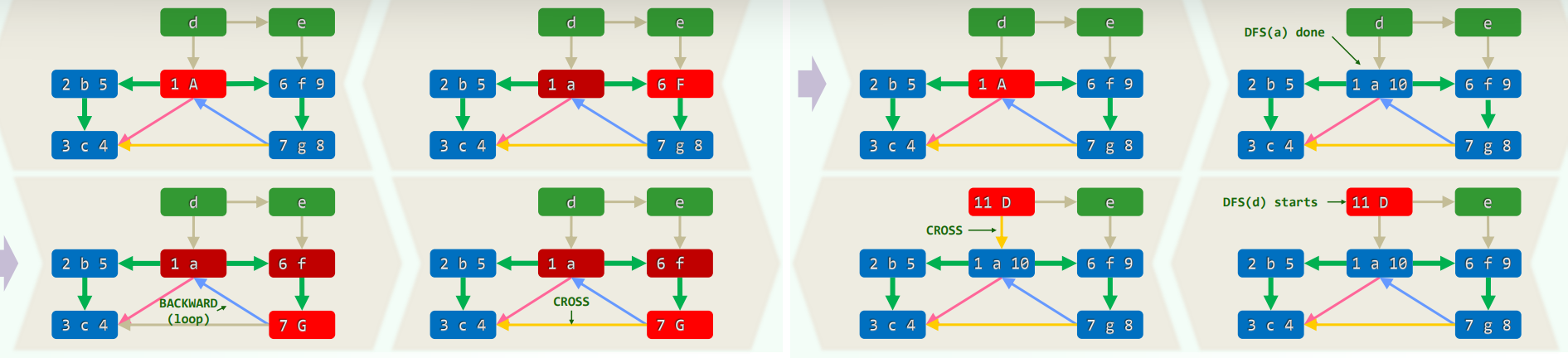
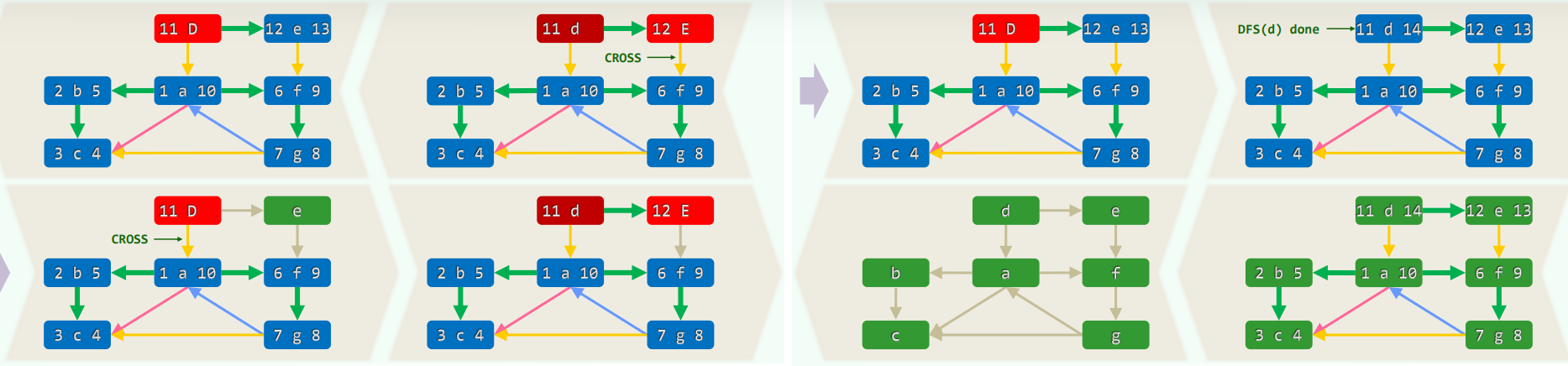
4.实例（有向图）

5.性质

5.1 DFS树/森林

从顶点s出发的DFS
- 在无向图中将访问与s连通的所有顶点（connectivity）
- 在有向图中将访问由s可达的所有顶点（reachability）
经DFS确定的树边，不会构成回路
从s出发的DFS，将以s为根生成一棵DFS树；所有DFS树，进而构成DFS森林
DFS树及森林由parent指针描述（只不过所有边取反向）

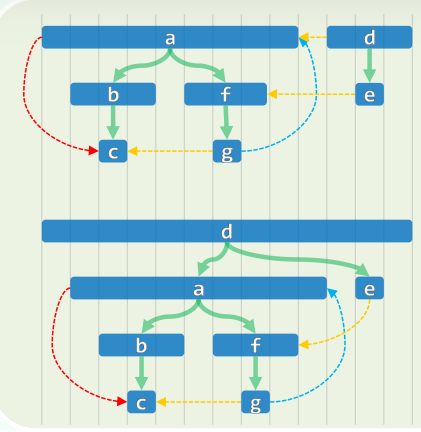
5.2 活跃期 & 括号引理

active[u]=(dTime[u],fTime[u])
括号定理（Parenthesis Lemma）：给定有向图G = (V, E)及其任一DFS森林，则
- u是v的后代 iff
- u是v的祖先 iff
- u与v“无关”iff
仅凭status[]、dTime[]和fTime[] 即可对各边分类.

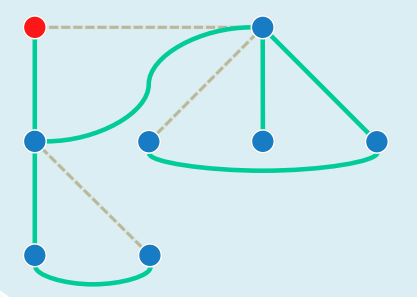
5.3 边分类

TREE(v, u)：可从当前v进入处于UNDISCOVERED状态的u

BACKWARD(v, u)：试图从当前v进入处于DISCOVERED状态的u，DFS发现后向边 iff 存在回路

FORWARD(v, u)：试图从当前顶点v进入处于VISITED状态的u，且v更早被发现

CROSS(v, u)：试图从当前顶点v进入处于VISITED状态的u，且u更早被发现

5.4 遍历算法应用举例

连通图的支撑树（DFS/BFS Tree）	DFS/BFS
非连通图的支撑森林	DFS/BFS
连通性检测	DFS/BFS
无向图环路检测/二部图判定	DFS/BFS
有向图环路检测	DFS
顶点之间可达性检测/路径求解	DFS/BFS
顶点之间的最短距离	BFS
直径/半径/围长/中心	BFS
欧拉回路	DFS
拓扑排序	DFS
双连通分量、强连通分量分解	DFS

六、拓扑排序

1.零入度算法

1.1 有向无环图（Directed Acyclic Graph）

应用
- 类派生和继承关系图中，是否存在循环定义
- 操作系统中相互等待的一组线程，如何调度
- 给定一组相互依赖的课程，设计可行的培养方案
- 给定一组相互依赖的知识点，设计可行的教学进度方案
- 项目工程图中，设计可串行施工的方案
- email系统中，是否存在自动转发或回复的回路

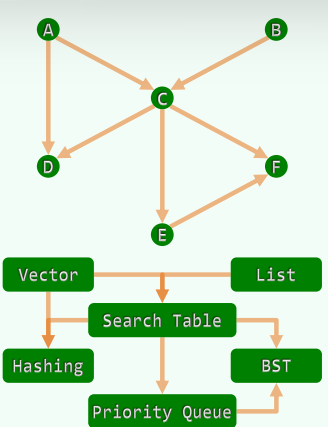
1.2 拓扑排序

任给有向图G（不一定是DAG），尝试将所有顶点排成一个线性序列，使其次序须与原图相容（每一顶点都不会通过边指向前驱顶点）
接口要求
- 若原图存在回路（即并非DAG），检查并报告
- 否则，给出一个相容的线性序列

1.3 偏序 ~ 极值

每个DAG对应于一个偏序集；拓扑排序对应于一个全序集所谓的拓扑排序，即构造一个与指定偏序集相容的全序集
可以拓扑排序的有向图，必定无环
任何DAG，都存在（至少）一种拓扑排序
有限偏序集必有极值元素

1.4 存在性

任何有向无环图g中必有一个零入度的顶点m
若g{m}存在拓扑排序S={ $v_{k_1},v_{k_2},...,v_{k_{n-1}}$ }，则 $S^{'}$ ={ $m,v_{k_1},v_{k_2},...,v_{k_{n-1}}$ }即为g的拓扑排序
只要m不唯一，拓扑排序也应不唯一

1.5 策略：顺序输出零入度顶点

将所有入度为零的顶点存入栈S，取空队列Q //O(n) 
while ( ! S.empty() ) { //O(n) 
    Q.enqueue( v = S.pop() ); //栈顶v转入队列 
    for each edge( v, u ) //v的邻接顶点u若入度仅为1 
        if ( u.inDegree < 2 ) S.push( u ); //则入栈 
    G = G \ { v }; //删除v及其关联边（邻接顶点入度减1） 
} //总体O(n + e) 
return |G| ? "NOT_A_DAG" ： Q; //残留的G空，当且仅当原图可拓扑排序

1.6 实例

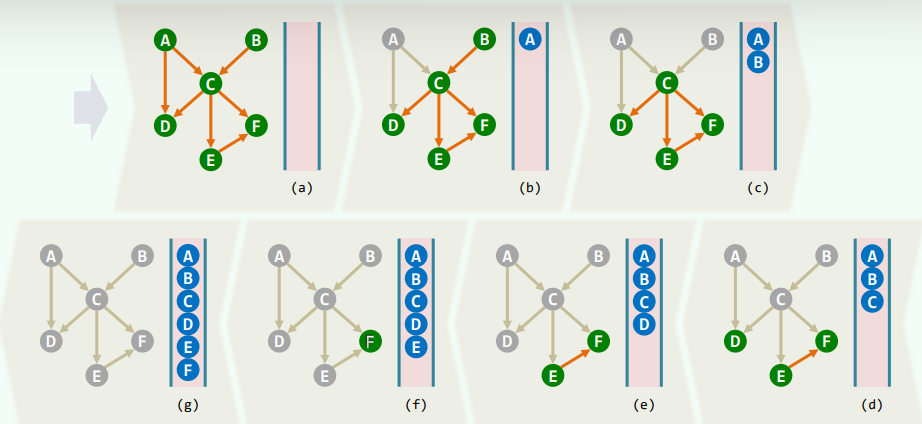
2.零出度算法

2.1 策略：逆序输出零出度顶点

//基于DFS，借助栈S 
对图G做DFS，其间 //得到组成DFS森林的一系列DFS树 
    每当有顶点被标记为VISITED，则将其压入S 
    一旦发现有后向边，则报告“NOT_A_DAG”并退出
DFS结束后，顺序弹出S中的各个顶点

各节点按fTime逆序排列，即是拓扑排序
复杂度与DFS相当，也是O(n+e)

2.2 实例

template<typename Tv,typename Te> //顶点类型、边类型 
bool Graph::TSort( Rank v, int & clock, Stack* S ) { 
    dTime(v) = ++clock; status(v) = DISCOVERED; //发现顶点v 
    for ( Rank u = firstNbr(v); u < UINT_MAX; u = nextNbr(v, u) ) //考查v的每一邻居u 
        switch ( status(u) ) { //并视u的状态分别处理 
            case UNDISCOVERED: 
                parent(u) = v; type(v, u) = TREE; 
                if ( ! TSort(u, clock, S) ) return false; 
                break; //从顶点u处深入 
            case DISCOVERED: //一旦发现后向边（非DAG） 
                type(v, u) = BACKWARD; 
                return false; //则退出而不再深入 
            default: //VISITED (digraphs only) 
                type(v, u) = dTime(v) < dTime(u) ? FORWARD : CROSS; break; 
        }
    status(v) = VISITED; S->push( vertex(v) ); //顶点被标记为VISITED时入栈 
    return true; 
}