数据结构（c++）学习笔记--优先级队列

---

一、概述

1.需求与动机

1.1循优先级访问

• 应用举例

  • 离散事件模拟
  • 操作系统：任务调度/中断处理/MRU/…
  • 输入法：词频调整

• 极值元素：须反复地、快速地定位

• 集合组成：可动态变化

• 元素优先级：可动态变化

• 作为底层数据结构所支持的高效操作是很多高效算法的基础

  • 内部、外部、在线排序
  • 贪心算法：Huffman编码、Kruskal
  • 平面扫描算法中的事件队列

1.2 优先级队列(priority queue)

template <typename T> struct PQ { //priority queue 
    virtual void insert( T ) = 0; 
    virtual T getMax() = 0; 
    virtual T delMax() = 0; 
}; //作为ADT的PQ有多种实现方式，各自的效率及适用场合也不尽相同

• Stack和Queue，都是PQ的特例——优先级完全取决于元素的插入次序
• Steap和Queap，也是PQ的特例——插入和删除的位置受限

2.基本实现

2.1 Vector

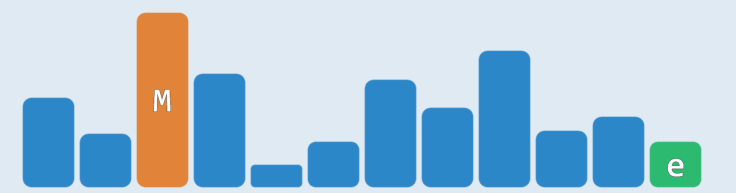
getMax()	delMax()	insert()
traverse(),Θ(n)	remove( traverse() ),Θ(n) + O(n) = (n)	insertAsLast(e),O(1)

2.2 Sorted Vector

getMax()	delMax()	insert()
[n − 1],O(1)	remove(n − 1),O(1)	insert( 1 + search(e), e ),O(logn) + O(n) = O(n)

2.3 List

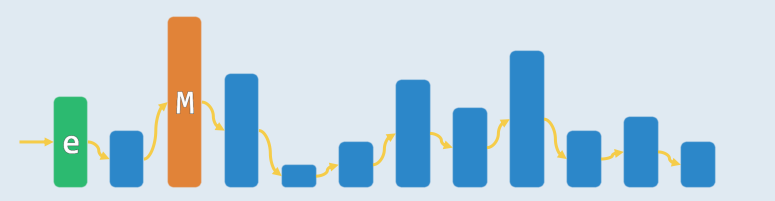
getMax()	delMax()	insert()
traverse(),Θ(n)	remove( traverse() ),Θ(n) + O(1) = Θ(n)	insertAsFirst(e) O(1)

2.4 Sorted List

getMax()	delMax()	insert()
first(),O(1)	remove( first() ),O(1)	insertA( search(e), e ),O(n) + O(1) = O(n)

2.5 BBST

• AVL、Splay、Red-black：三个接口均只需O(logn)时间。但是，BBST的功能远远超出了PQ的需求

• PQ = 1 × insert() + 0.5 × search() + 0.5 × remove()

• 若只需查找极值元，则不必维护所有元素之间的全序关系，偏序足矣

• 因此有理由相信，存在某种更为简单、维护成本更低的实现方式，使得各功能接口的时间复杂度依然为O(logn)，而且实际效率更高

• 当然，就最坏情况而言，这类实现方式已属最优

2.6 统一测试

template<typename PQ,typenaem T> void testHeap( int n ) { 
    T* A = new T[ 2 * n / 3 ]; //创建容量为2n/3的数组，并 
    for ( int i = 0; i < 2 * n / 3; i++ ) A[i] = dice( (T) 3 * n ); //随机化 
    PQ heap( A + n / 6, n / 3 ); delete [] A; //Robert Floyd 
    while ( heap.size() < n ) //随机测试 
        if ( dice( 100 ) < 70 ) heap.insert( dice( (T) 3 * n ) ); //70%概率插入 
        else if ( ! heap.empty() ) heap.delMax(); //30%概率删除 
    while ( ! heap.empty() ) heap.delMax(); //清空 统一测试
}

二、完全二叉堆

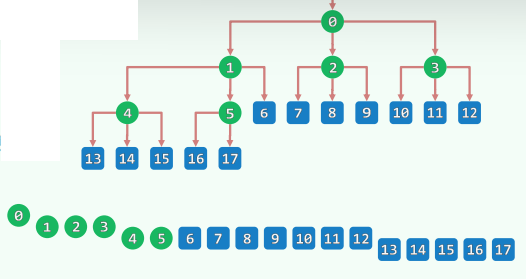
1.结构

1.1 结构性：逻辑元素、物理节点依层次遍历次序彼此对应

• #define Parent(i) ( ((i) - 1) >> 1 )

• #define LChild(i) ( 1 + ((i) << 1) )

• #define RChild(i) ( (1 + (i)) << 1 )

• 逻辑上，等同于完全二叉树；物理上，直接借助向量实现

• 内部节点的最大秩$=\lfloor (n-2)/2\rfloor =\lceil (n-3)/2\rceil$

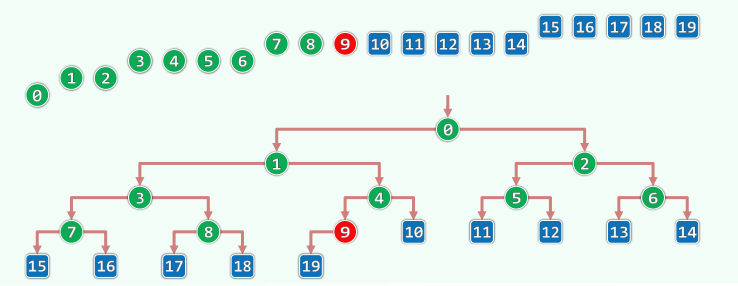
1.2 PQ_ComplHeap = PQ + Vector

template<typename T> struct PQ_ComplHeap : public PQ<T>, public Vector<T> { 
PQ_ComplHeap( T* A, Rank n ) { copyFrom( A, 0, n ); heapify( _elem, n ); } 
void insert( T ); T getMax(); T delMax(); 
}; 

template<typename T> Rank percolateDown( T* A, Rank n, Rank i ); //下滤 

template<typename T> Rank percolateUp( T* A, Rank i ); //上滤

template<typename T> void heapify( T* A, Rank n); //Floyd建堆算法

1.3 堆序性

templat<typename T> T PQ_ComplHeap<T>::getMax() { return _elem[0]; }

• 只要 0<i，必满足 H[ i ]≤H[ Parent(i) ]，故H[0]即是全局最大

2.插入

2.1 算法：逐层上滤

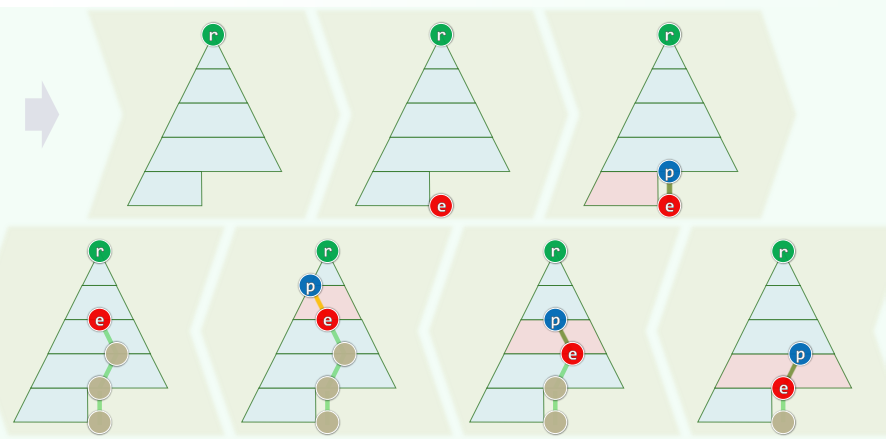
2.2 实例

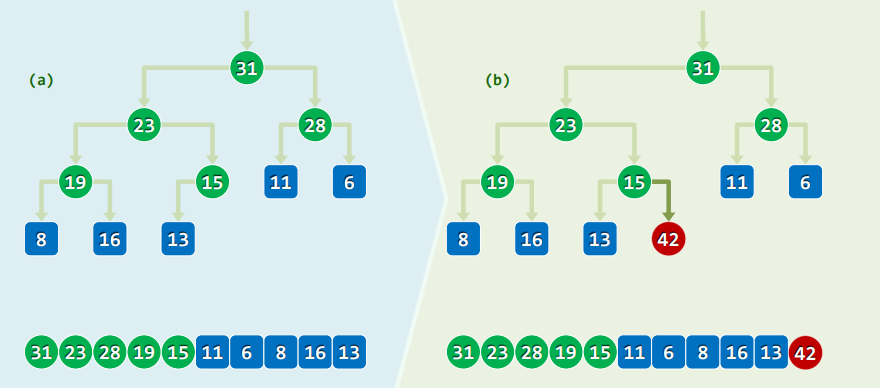
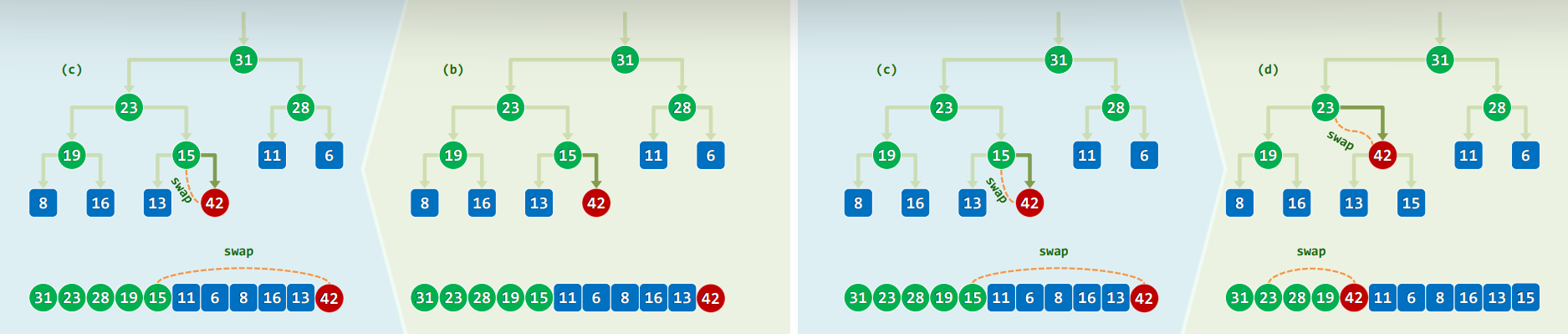
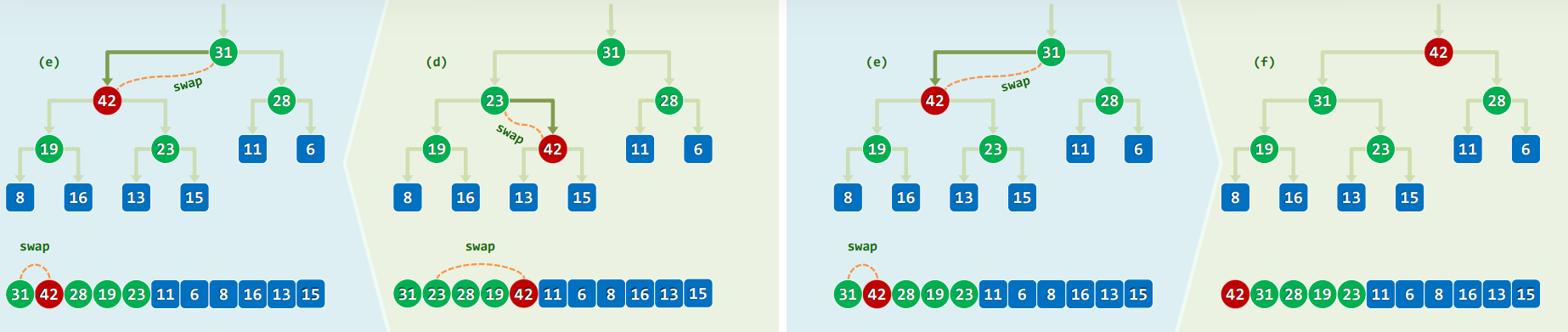
2.3 实现

template<typenaem T> void PQ_ComplHeap<T>::insert( T e ) //插入 
    { Vector<T>::insert( e ); percolateUp( _elem, _size - 1 ); } //此insert()非彼 

template<typenaem T> Rank percolateUp( T* A, Rank i ) { //0 <= i < _size 
    while ( 0 < i ) { //在抵达堆顶之前，反复地 
        Rank j = Parent( i ); //考查[i]之父亲[j] 
        if ( lt( A[i], A[j] ) ) break; //一旦父子顺序，上滤旋即完成；否则 
        swap( A[i], A[j] ); i = j; //父子换位，并继续考查上一层 
    }
    return i; //返回上滤最终抵达的位置 
}

2.4 效率

• e在上滤过程中，只可能与祖先们交换
• 完全树必平衡，e的祖先不超过$O(\log n)$个
• 故知插入操作可在$O(\log n)$时间内完成
• 然而就数学期望而言 实际效率往往远远更高

3.删除

3.1 算法：割肉补疮 + 逐层下滤

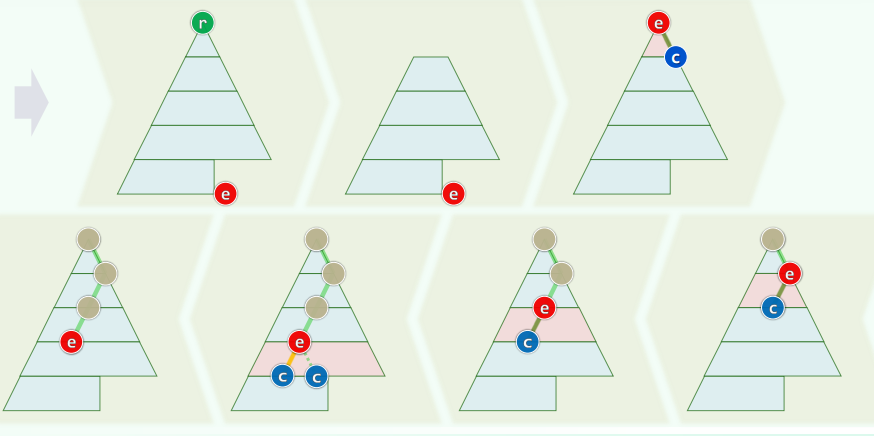
3.2 实例

3.3 实现

template<typename T> T PQ_ComplHeap<T>::delMax() { //删除 
    T maxElem = _elem[0]; _elem[0] = _elem[ --_size ]; //摘除堆顶，代之以末词条 
    percolateDown( _elem, _size, 0 ); //对新堆顶实施下滤 
    return maxElem; //返回此前备份的最大词条 
} 

template<typename T> Rank percolateDown( T* A, Rank n, Rank i ) { //0 <= i < n 
    Rank j; //i及其（至多两个）孩子中，堪为父者 
    while ( i != ( j = ProperParent( A, n, i ) ) ) //只要i非j，则 
        { swap( A[i], A[j] ); i = j; } //换位，并继续考察i 
    return i; //返回下滤抵达的位置（亦i亦j） 
}

3.4 效率

• e在每一高度至多交换一次,累计交换不超过$O(\log n)$次
• 通过下滤，可在$O(\log n)$时间内删除堆顶节点，并整体重新调整为堆

4.批量建堆

4.1 自上而下的上滤

PQ_ComplHeap( T* A, Rank n ) { 
    copyFrom( A, 0, n ); 
    heapify( _elem, n ); 
}

template<typename T> void heapify( T* A, const Rank n ) { //蛮力 
    for ( Rank i = 1; i < n; i++ ) //按照逐层遍历次序逐一 
        percolateUp( A, i ); //经上滤插入各节点 
}

4.2 效率

• 最坏情况下
  • 每个节点都需上滤至根
  • 所需成本线性正比于其深度
• 即便只考虑底层n/2个叶节点，深度均为$O(\log n)$累计耗时$O(n\log n)$
• 这样长的时间，本足以全排序

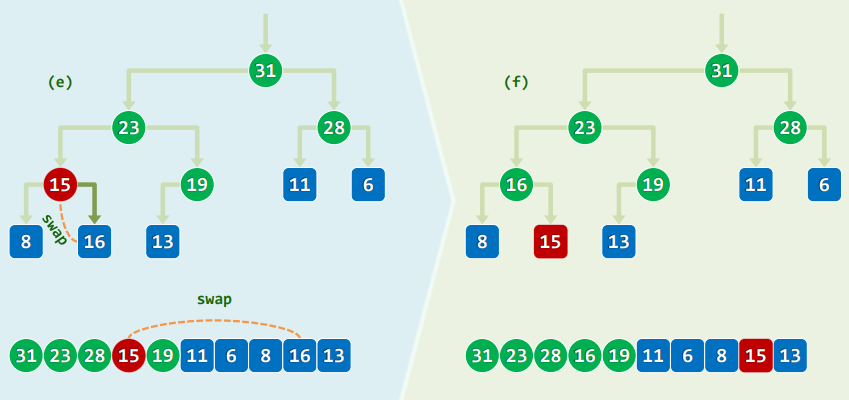
4.3 自下而上的下滤

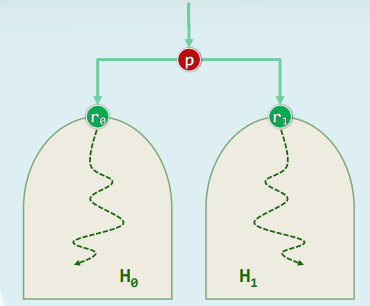
• 任意给定堆$H_1$和$H_0$，以及节点p
• 为得到堆 H 0 ∪ { p } ∪ H 1 H_0∪\{p\}∪H_1 H0​∪{p}∪H1​，只需将$r_0$和$r_1$当作p的孩子，再对p下滤

template<typename T>
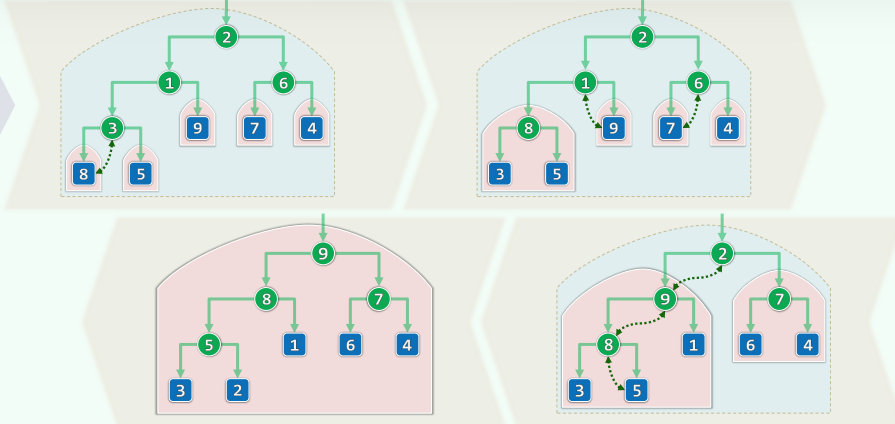
void heapify( T* A, Rank n ) { //自下而上 
    for ( Rank i = n/2 - 1; 0 <= i; i-- ) //依次 
        percolateDown( A, n, i ); //下滤各内部节点 
} //可理解为子堆的逐层合并，堆序性最终必然在全局恢复

4.4 实例

4.5 效率

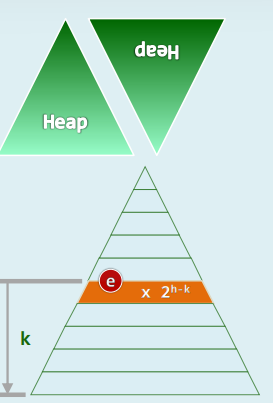
• 每个内部节点所需的调整时间，正比于其高度而非深度
• 不失一般性，考查满树： $n=2^{h+1}-1$
• 所有节点的高度总和 S ( n ) = ∑ k = 1 h k ⋅ 2 h − k = ∑ k = 1 h ∑ i = 1 h 2 h − k = ∑ k = 1 h ∑ i = 1 h 2 h − k = ∑ i = 1 h ∑ k = 0 h − i { 2 h − i + 1 − 1 } = ∑ i = 1 h 2 h − i + 1 − h = ∑ i = 1 h 2 i − h = 2 h + 1 − 2 − h = O ( n ) S(n)=\sum_{k=1}^h k·2^{h-k}=\sum_{k=1}^h\sum_{i=1}^h 2^{h-k}=\sum_{k=1}^h\sum_{i=1}^h 2^{h-k}=\sum_{i=1}^h\sum_{k=0}^{h-i}\{2^{h-i+1}-1\}=\sum_{i=1}^h 2^{h-i+1}-h=\sum_{i=1}^h2^i-h=2^{h+1}-2-h=O(n) S(n)=∑k=1h​k⋅2h−k=∑k=1h​∑i=1h​2h−k=∑k=1h​∑i=1h​2h−k=∑i=1h​∑k=0h−i​{2h−i+1−1}=∑i=1h​2h−i+1−h=∑i=1h​2i−h=2h+1−2−h=O(n)

三、堆排序

1.选取

• 在selectionSort()中将U替换为H
• 初始化 ： heapify()，O(n)
• 迭代 ： delMax()，$O(\log n)$
• 不变性 ： H≤S
• $O(n)+n\cdot O(\log n)=O(n\log n)$

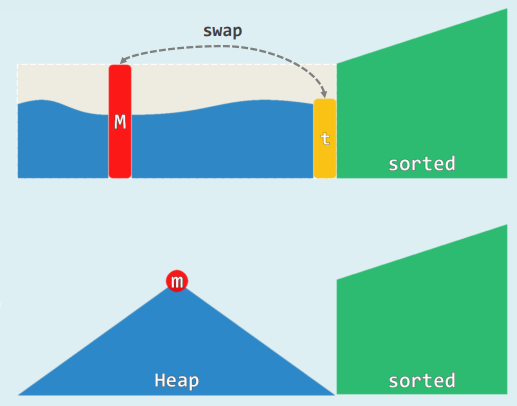
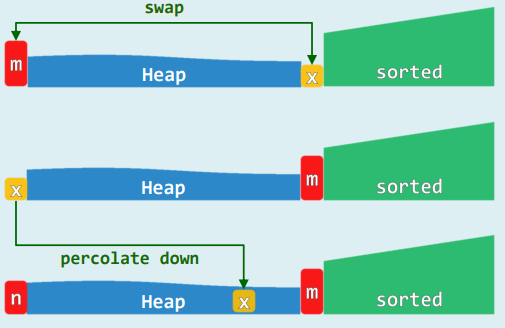
2.就地

• 在物理上 完全二叉堆即是向量
• 既然此前有：
  • m = H[ 0 ]
  • x = H[ n − 1 ]
• 不妨随即就： swap( m , x ) = H.insert( x ) + S.insert( m )

3.实现

template<typename T> //对向量区间[lo, hi)做就地堆排序 
void Vector::heapSort( Rank lo, Rank hi ) { 
    T* A = _elem + lo; Rank n = hi - lo; heapify( A , n ); //待排序区间建堆，O(n) 
    while ( 0 < --n ) //反复地摘除最大元并归入已排序的后缀，直至堆空 
        { swap( A[0], A[n] ); percolateDown( A, n, 0 ); } //堆顶与末元素对换后下滤
}

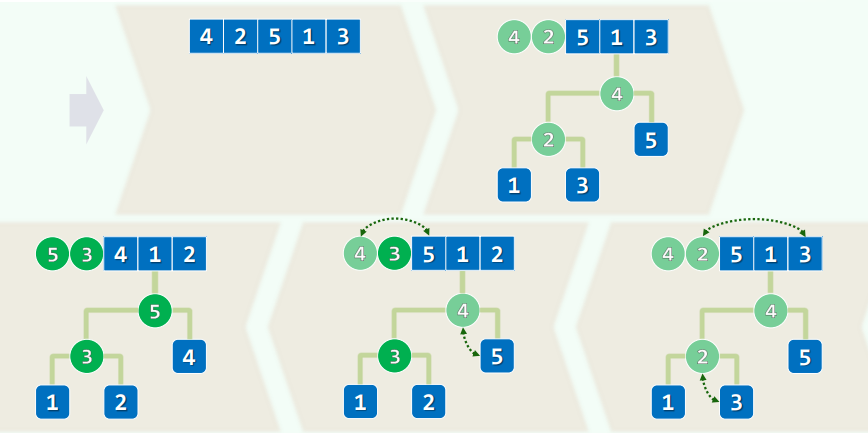
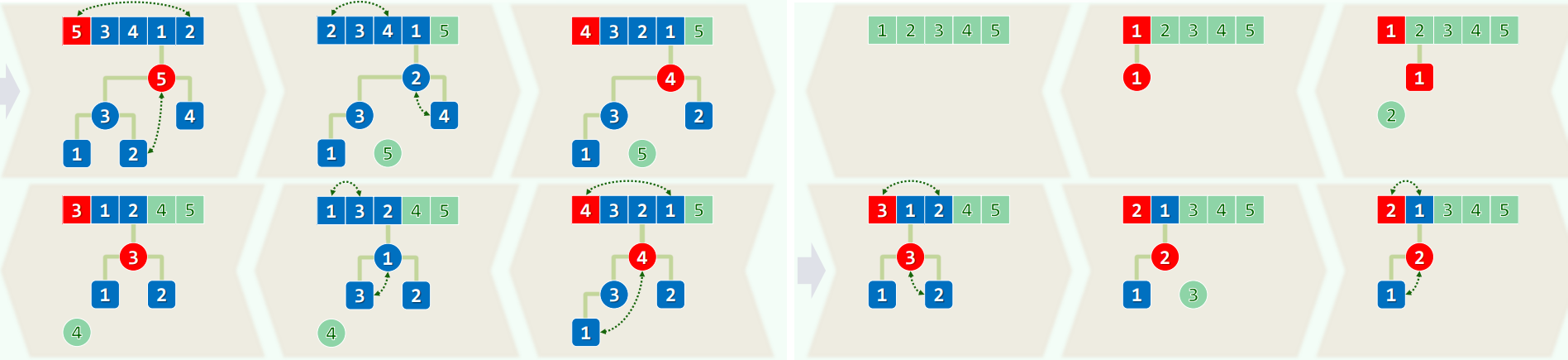
4.实例

四、多叉堆

1.优先级搜索

• 无论何种算法，差异仅在于所采用的优先级更新器prioUpdater()
  • Prim算法： g->pfs( 0, PrimPU() );
  • Dijkstra算法： g->pfs( 0, DijkPU() );
• 每一节点引入遍历树后，都需要更新树外顶点的优先级（数），并选出新的优先级最高者
• 若采用邻接表，两类操作的累计时间，分别为$O(n+e)$和$O(n^2)$

2.优先级队列

• 自然地，PFS中的各顶点可组织为优先级队列
• 为此需要使用PQ接口
  • heapify(): 由n个顶点创建初始PQ，总计O(n)
  • delMax(): 取优先级最高（极短）跨边(u, w)，总计$O( n * \log n ) $
  • increase(): 更新所有关联顶点到U的距离，提高优先级，总计$O(e\ast \log n)$
• 总体运行时间 = O( (n+e)*logn )
  • 对于稀疏图，处理效率很高
  • 对于稠密图，反而不如常规实现的版本

3.多叉堆

• 仍可基于向量实现，且父、子节点的秩可简明地相互换算

  • $parent(k)=\lfloor (k-1)/d\rfloor$
  • $child(k,i)=k\cdot d+i,0\le i\le d$//d不是2的幂时，不能借助移位加速秩的换算

• heapify()：O(n) //不可能再快了

• delMax()：$O(\log n)$ //实质就是percolateDown()，已是极限了

• increase()：$O(\log n)$ //实质就是percolateUp()–仍有改进空间

4.上山容易下山难

• 若将二叉堆改成多叉堆（d-heap）,则堆高降至$O({\log }_{d}n)$
• 相应地，上滤成本降至$ \log_d n$
• 但（只要d>4）下滤成本却增至$d\cdot lo{g}_{d}n=d\cdot \ln n/\ln d$

5.PFS

• 如此，PFS的运行时间将是：$n\cdot d\cdot lo{g}_{d}n+e\cdot {\log }_{d}n=(n\cdot d+e)\cdot {\log }_{d}n$

• 取$d\approx e/n+2$时,总体性能达到最优：$O(e\cdot {\log }_{e/(n+2)}n)$

• 对于稀疏图保持高效：$e\cdot {\log }_{e/(n+2)}n\approx n\cdot {\log }_{n/(n+2)}n=O(n\log n)$

• 对于稠密图改进极大：$e\cdot {\log }_{e/(n+2)}n\approx n^2\cdot {\log }_{n^2/(n+2)}n\approx n^2=O(e)$

• 对于一般的图，会自适应地实现最优

五、左式堆

1.沿藤合并

1.1 堆合并

• H = merge(A, B)：将堆A和B合二为一 //不妨设|A| = n ≥ m = |B|
• 方法一：$A.insert(B.delMax()),O(m\ast (\log m+\log (n+m)))=O(m\ast \log (n+m))$
• 方法二：$union(A,B).heapify(n+m),O(m+n)$

1.2 两堆合并 = 二路归并

1.3 简捷 = 统一沿右侧藤

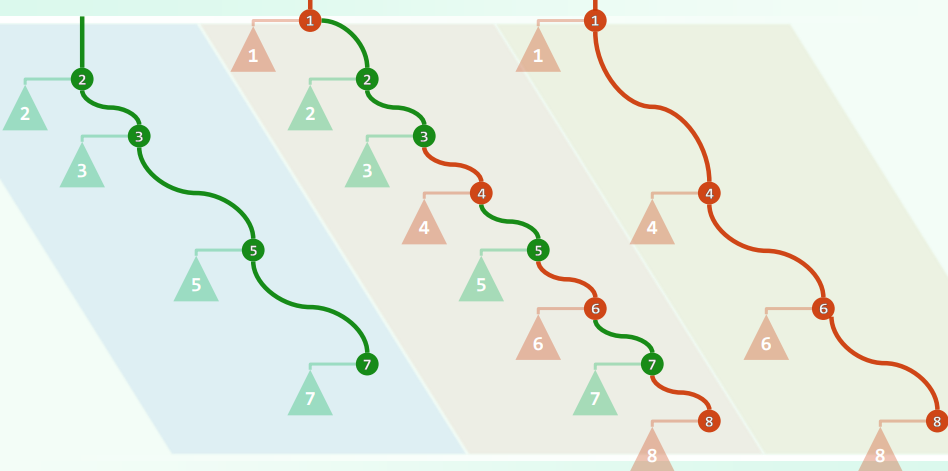
1.4 递归实现

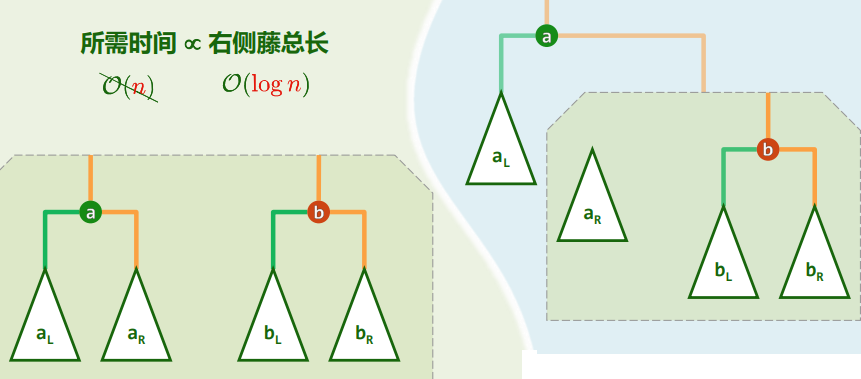
2.NPL与控制藤长

2.1 可持续 = 单侧倾斜

• 保持堆序性，附加新条件，使得在堆合并过程中，只涉及少量节点：$O(\log n)$
• 新条件 = 单侧倾斜：节点分布偏向于左侧,合并操作只涉及右侧
• 则拓扑上不见得是完全二叉树，结构性无法保证
• 实际上，结构性并非堆结构的本质要求

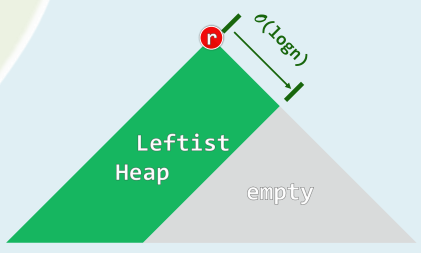
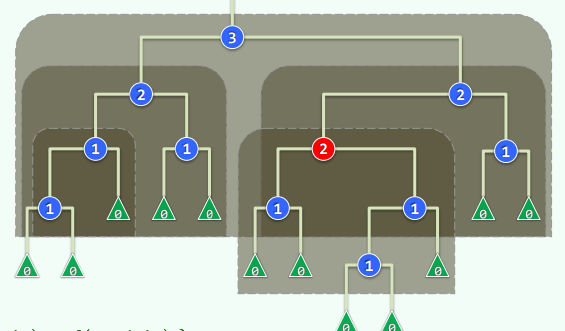
2.2 空节点路径长度

• 引入所有的外部节点，消除一度节点，转为真二叉树
• Null Path Length
  • npl(NULL)=0
  • npl(x)=1+min{npl(lc(x)),npl(rc(x))}
• 验证： npl(x) = x到外部节点的最近距离 = 以x为根的最大满子树的高度

2.3 左式堆=处处左倾

• 对任何内节点x，都有：npl(lc(x)≥npl(rc(x))

• 推论：npl(x)=1+npl(rc(x))

• 左倾性与堆序性，相容而不矛盾

• 左式堆的子堆，必是左式堆

• 左式堆倾向于更多节点分布于左侧分支

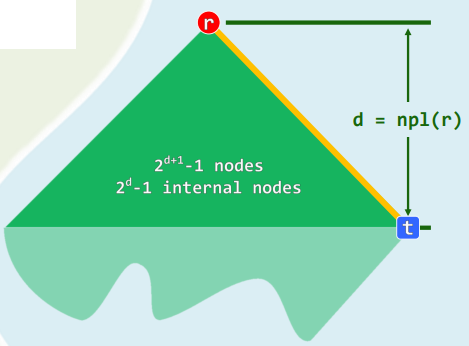
2.4 右侧链

• rChain(x)：从节点x出发，一直沿右分支前进
• 特别地，rChain®的终点，即全堆中最浅的外部节点
  • $npl(r)\equiv |rChain(r)|=d$
  • 存在一棵以r为根、高度为d的满子树
• 右侧链长为d的左式堆，至少包含
  • $2^d - 1 $个内部节点
  • $2^{ d+1} - 1 $个节点
• 反之，包含n个节点的左式堆，右侧链长度$d\le \lfloor {\log }_2(n+1)-1\rfloor =O(\log n)$

3.合并算法

3.1 左式堆（LeftHeap）

template<typename T> //基于二叉树，以左式堆形式实现的优先级队列 
class PQ_LeftHeap : public PQ<T>, public BinTree<T> { 
public: 
    T getMax() { return _root->data; } 
    void insert(T); T delMax(); //均基于统一的合并操作实现... 
    PQ_LeftHeap( PQ_LeftHeap & A, PQ_LeftHeap & B ) { 
        _root = merge(A._root, B._root); _size = A._size + B._size; 
        A._root = B._root = NULL; A._size = B._size = 0; 
    } 
}; 

template<typename T> BinNodePosi<T> merge(BinNodePosi<T>, BinNodePosi<T>);

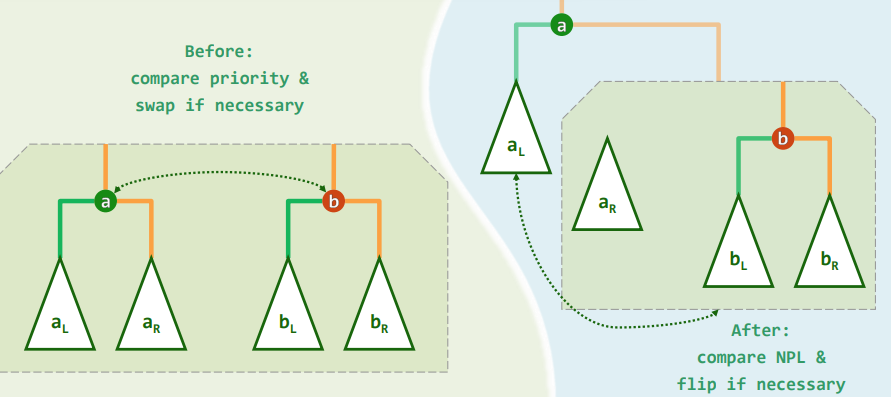
3.2 递归：前处理 + 后处理

3.3 递归实现

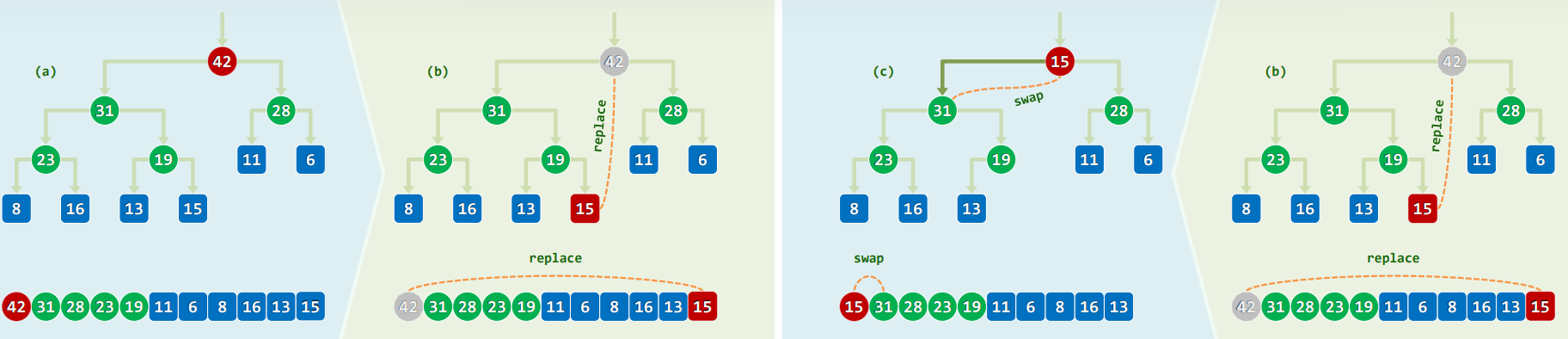
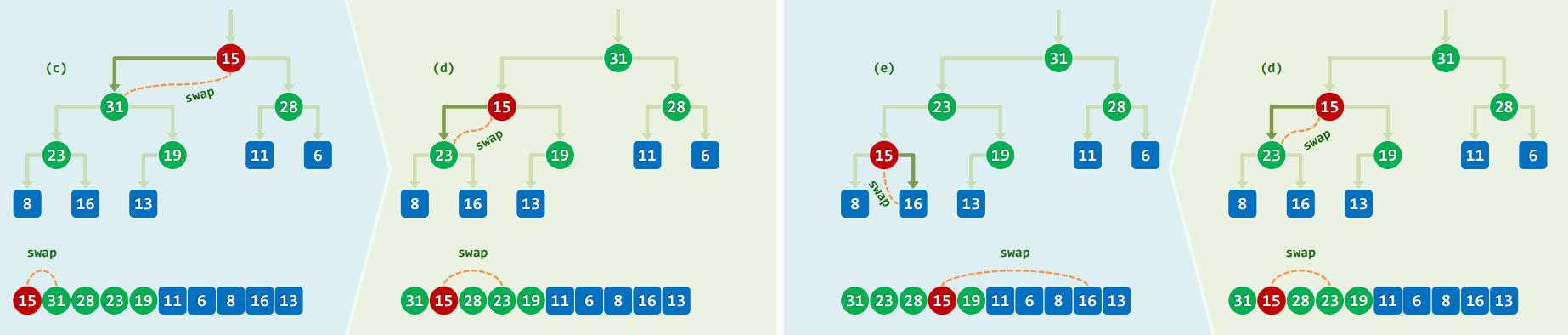
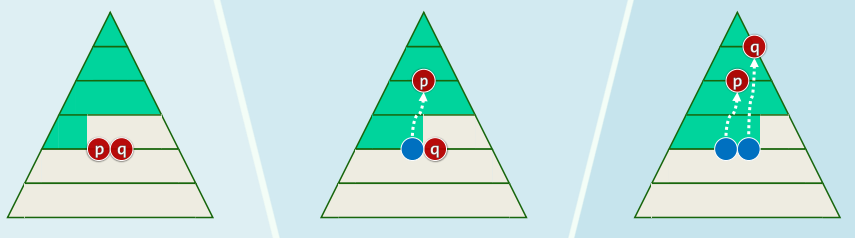
template <typename T> BinNodePosi<T> merge( BinNodePosi<T> a, BinNodePosi<T> b ) { 
    if ( !a ) return b; if ( !b ) return a; //递归基 
    if ( lt( a->data, b->data ) ) swap( a, b ); //确保a>=b 
        ( a->rc = merge( a->rc, b ) )->parent = a; //将a的右子堆，与b合并 
    if ( ! a->lc || a->lc->npl < a->rc->npl ) //若有必要 
        swap( a->lc, a->rc ); //交换a的左、右子堆，以确保左子堆的npl不小 
    a->npl = a->rc ? 1 + a->rc->npl : 1; //更新a的npl 
    return a; //返回合并后的堆顶 
}

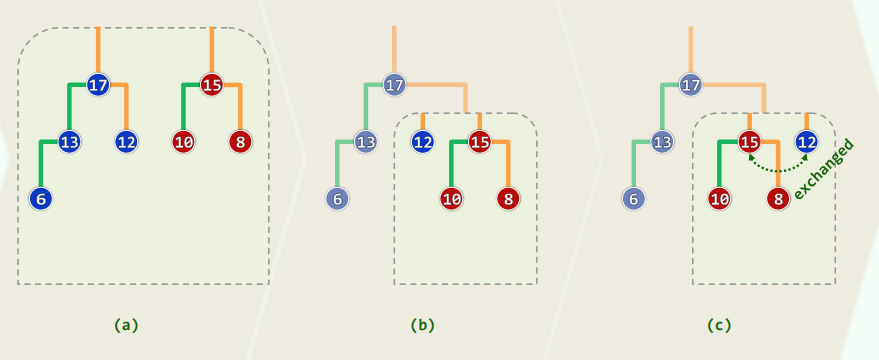
3.4 实例

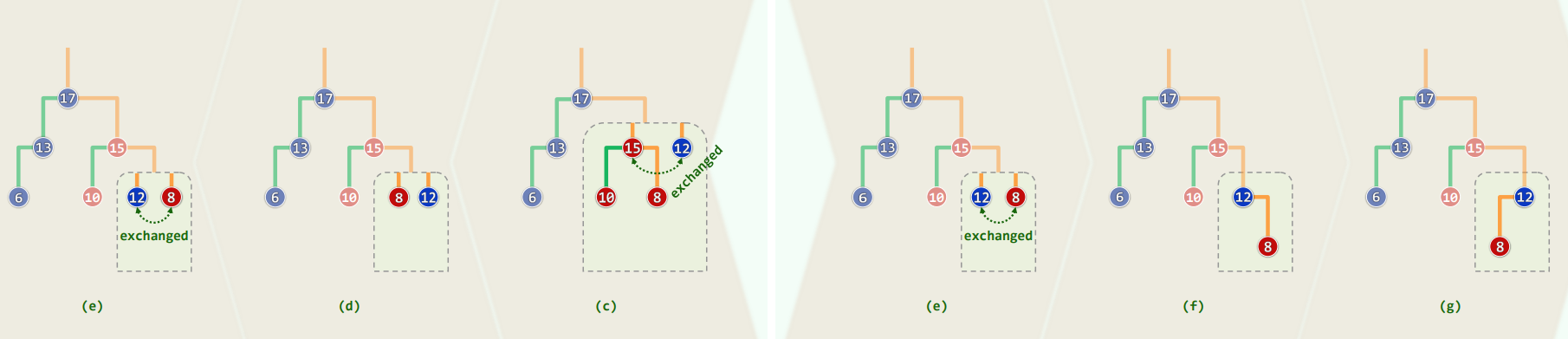
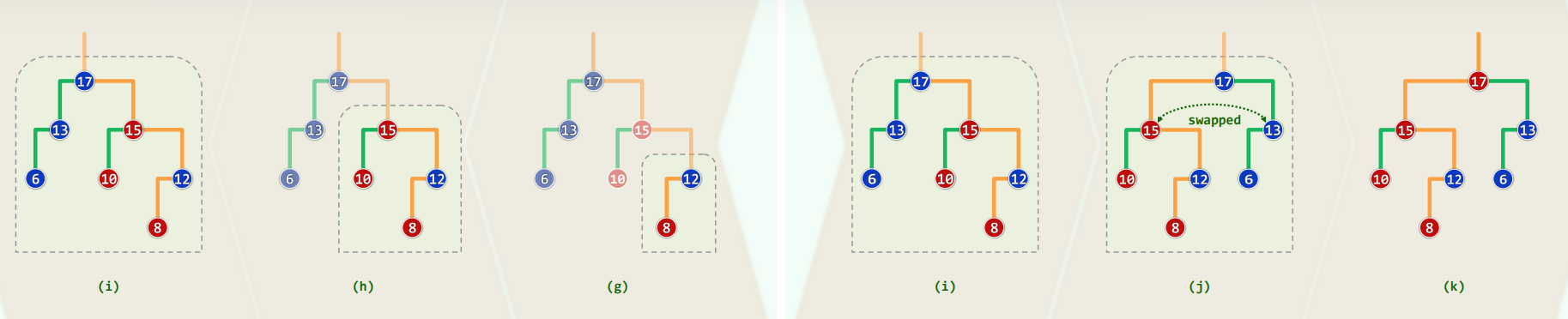
3.5 迭代实现

template <typename T> BinNodePosi<T> merge( BinNodePosi<T> a, BinNodePosi<T> b ) { 
    if ( !a ) return b; if ( !b ) return a; //退化情况 
    if ( lt( a->data, b->data ) ) swap( a, b ); //确保a>=b 
    for ( ; a->rc; a = a->rc ) //沿右侧链做二路归并，直至堆a->rc先于b变空 
        if ( lt( a->data, b->data ) ) { b->parent = a; swap( a->rc, b); } //接入b 
    (a->rc = b)->parent = a; //直接接入b的残余部分（必然非空） 
    for ( ; a; b = a, a = a->parent ) { //从a出发沿右侧链逐层回溯（b == a->rc） 
        if ( !a->lc || a->lc->npl < a->rc->npl ) swap( a->lc, a->rc ); //确保npl合法 
        a->npl = a->rc ? a->rc->npl + 1 : 1; //更新npl 
    } 
    return b; //返回合并后的堆顶 
}

4.插入与删除

4.1 插入

template <typename T> void PQ_LeftHeap<T>::insert( T e ) { //O(logn) 
    _root = merge( _root, new BinNode<T>( e, NULL ) );
    _size++; 
}

4.2 删除

template <typename T> T PQ_LeftHeap<T>::delMax() { //O(logn) 
    BinNodePosi<T> lHeap = _root->lc; if (lHeap) lHeap->parent = NULL; 
    BinNodePosi<T> rHeap = _root->rc; if (rHeap) rHeap->parent = NULL; 
    T e = _root->data; 
    delete _root; _size--; 
    _root = merge( lHeap, rHeap ); 
    return e; 
}