文章目录
一、快速排序
1.轴点
1.1 分而治之
- 轴点(pivot):左侧/右侧的元素,均不比它更大/更小
- 以轴点为界,自然划分:max( [0, mi) ) ≤ min( (mi, hi) )
- 前缀、后缀各自(递归)排序之后,原序列自然有序
- sorted(S) = sorted(SL) + sorted(SR)
- 归并排序(mergesort)难点在于合,而快速排序(quicksort)在于分
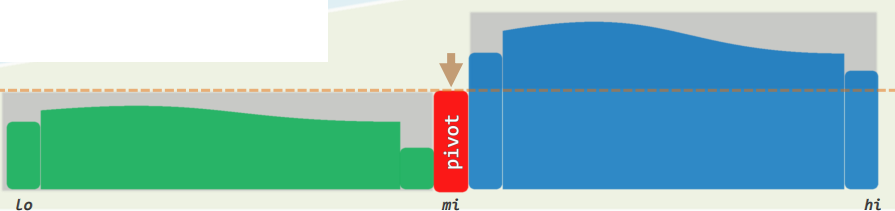
1.2 快速排序
template <typename T> void Vector<T>::quickSort( Rank lo, Rank hi ) {
if ( hi - lo < 2 ) return;
Rank mi = partition( lo, hi );
quickSort( lo, mi );
quickSort( mi + 1, hi );
}
1.3 轴点
- 必要条件: 轴点必定已然就位
- 特别地: 在有序序列中,所有元素皆为轴点,反之亦然
- 快速排序: 就是将所有元素逐个转换为轴点的过程
- 絮乱(derangement): 任何元素都不在原位。比如,顺序序列循环移位
- 不需很多交换,即可使任一元素转为轴点
2.快速划分:LUG版
2.1 减而治之,相向而行
-
任取一个候选者(如[0])
-
L + U + G
-
交替地向内移动lo和hi
-
逐个检查当前元素: 若更小/大,则转移归入L/G
-
当lo = hi时,只需 将候选者嵌入于L、G之间,即成轴点
-
各元素最多移动一次(候选者两次) ——累计O(n)时间、O(1)辅助空间
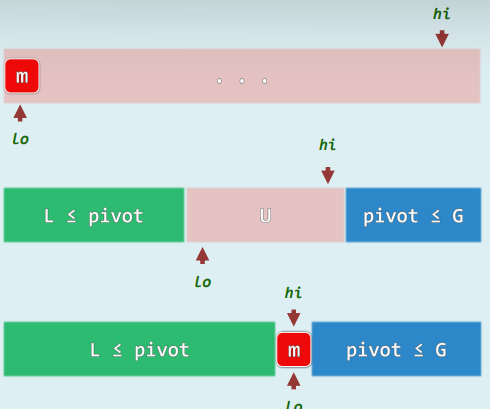
2.2 快速划分:LUG版
template <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi)
swap( _elem[ lo ], _elem[ lo + rand() % ( hi - lo ) ] ); //随机交换
hi--; T pivot = _elem[ lo ]; //经以上交换,等效于随机选取候选轴点
while ( lo < hi ) { //从两端交替地向中间扫描,彼此靠拢
while ( lo < hi && pivot <= _elem[ hi ] ) hi--; //向左拓展G
_elem[ lo ] = _elem[ hi ]; //凡小于轴点者,皆归入L
while ( lo < hi && _elem[ lo ] <= pivot ) lo++; //向右拓展L
_elem[ hi ] = _elem[ lo ]; //凡大于轴点者,皆归入G
} //assert: lo == hi
_elem[ lo ] = pivot; return lo; //候选轴点归位;返回其秩
}
2.3 不变性 + 单调性:L ≤ pivot ≤ G; U = [lo, hi]中,[lo]和[hi]交替空闲
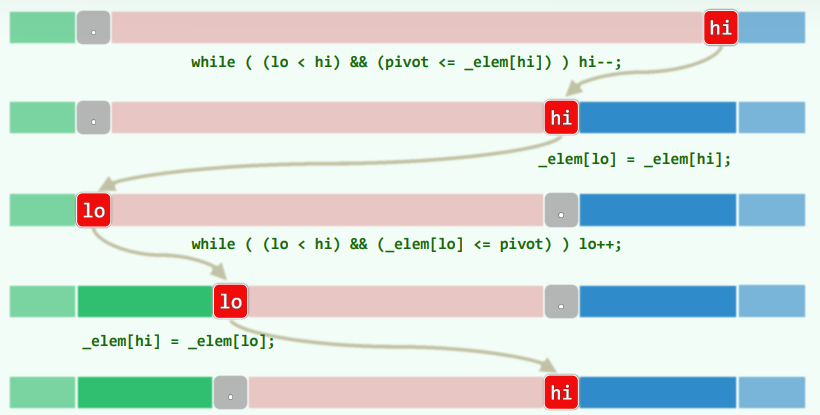
2.4 实例
- 线性时间:尽管lo、hi交替移动,累计移动距离不过O(n)
- in-place只需O(1)附加空间
- unstable
- lo/hi的移动方向相反
- 左/右侧的大/小重复元素可能前/后颠倒

3.迭代、贪心与随机
3.1 空间复杂度 ~ 递归深度
- 最好:划分总均衡 O ( log n ) O(\log n) O(logn)
- 最差:划分皆偏侧 O ( n ) O(n) O(n)
- 平均:均衡不致太少 O ( log n ) O(\log n) O(logn)
3.2 非递归 + 贪心
#define Put( K, s, t ) { if ( 1 < (t) - (s) ) { K.push(s); K.push(t); } }
#define Get( K, s, t ) { t = K.pop(); s = K.pop(); }
template <typename T> void Vector<T>::quickSort( Rank lo, Rank hi ) {
Stack<Rank> Task; Put( Task, lo, hi ); //等效于对递归树的先序遍历
while ( ! Task.empty() ) {
Get( Task, lo, hi ); Rank mi = partition( lo, hi );
if ( mi-lo < hi-mi ) { Put( Task, mi+1, hi ); Put( Task, lo, mi ); }
else { Put( Task, lo, mi ); Put( Task, mi+1, hi ); }
} //大|小任务优先入|出栈,可保证(辅助栈)空间不过O(logn) 非递归
}
3.3 时间性能 + 随机
- 最好情况:每次划分都(接近)平均,轴点总是(接近)中央 —— 到达下界
- T ( n ) = 2 ⋅ T ( ( n − 1 ) / 2 ) + O ( n ) = O ( n ⋅ log n ) T(n)=2·T((n-1)/2)+O(n)=O(n·\log n) T(n)=2⋅T((n−1)/2)+O(n)=O(n⋅logn)
- 最坏情况:每次划分都极不均衡(比如,轴点总是最小/大元素) —— 与起泡排序相当
- T ( n ) = T ( n − 1 ) + T ( 0 ) + O ( n ) = O ( n 2 ) T(n)=T(n-1)+T(0)+O(n)=O(n^2) T(n)=T(n−1)+T(0)+O(n)=O(n2)
- 采用随机选取(Randomization)、三者取中(Sampling)之类的策略,只能降低最坏情况的概率,而无法杜绝
4.递归深度
4.1 居中 + 偏侧
- 最坏情况( Ω ( n ) Ω(n) Ω(n)递归深度),概率极低
- 平均情况( O ( log n ) O(\log n) O(logn)递归深度),概率极高

- 实际上:除非过于侧偏的pivot,都会有效地缩短递归深度
- 准居中:pivot落在宽度为λ·n的居中区间 (λ也是这种情况出现的概率)
- 每一递归路径上,至多出现 log 2 / ( 1 + λ ) n \log_{2/(1+λ)}n log2/(1+λ)n个准居中的pivots
4.2 期望深度
- 每递归一层,都有λ(1-λ)的概率准居中(准偏侧)
- 深入 ( 1 / λ ) ⋅ log 2 / ( 1 + λ ) n (1/λ)·\log_{2/(1+λ)}n (1/λ)⋅log2/(1+λ)n层后,即可期望出现 log 2 / ( 1 + λ ) n \log_{2/(1+λ)}n log2/(1+λ)n次准居中,且有极高的概率出现
- 相反情况的概率 < ( 1 − λ ) ( 1 / λ − 1 ) ⋅ log 2 / ( 1 + λ ) n = n ( 1 / λ − 1 ) ⋅ log 2 / ( 1 + λ ) ( 1 − λ ) <(1-λ)^{(1/λ -1)·\log_{2/(1+λ)}n}=n^{(1/λ -1)·\log_{2/(1+λ)}(1-λ)} <(1−λ)(1/λ−1)⋅log2/(1+λ)n=n(1/λ−1)⋅log2/(1+λ)(1−λ),且随着λ增加而下降,比如λ>1/3之后,即至少有 1 − n 2 ⋅ log 3 / 2 ( 2 / 3 ) = 1 − n − 2 1-n^{2·\log_{3/2}(2/3)}=1-n^{-2} 1−n2⋅log3/2(2/3)=1−n−2的概率,使得递归深度不超过 ( 1 / λ ) ⋅ log 2 / ( 1 + λ ) n = 3 ⋅ log 3 / 2 n ≈ 5.129 ⋅ log n (1/λ)·\log_{2/(1+λ)}n=3·\log_{3/2}n≈5.129·\log n (1/λ)⋅log2/(1+λ)n=3⋅log3/2n≈5.129⋅logn
5.比较次数
5.1 递推分析
- 记期望的比较次数为T(n):T(1)=0,T(2)=1

T ( n ) = ( n − 1 ) + ( 1 / n ) ⋅ ∑ k = 0 n − 1 [ T ( k ) + T ( n − k − 1 ) ] = ( n − 1 ) + ( 2 / n ) ⋅ ∑ k = 0 n − 1 T ( k ) T(n)=(n-1)+(1/n)·\sum_{k=0}^{n-1}[T(k)+T(n-k-1)]=(n-1)+(2/n)·\sum_{k=0}^{n-1}T(k) T(n)=(n−1)+(1/n)⋅∑k=0n−1[T(k)+T(n−k−1)]=(n−1)+(2/n)⋅∑k=0n−1T(k)
n ⋅ T ( n ) = n ⋅ ( n − 1 ) + 2 ⋅ ∑ k = 0 n − 1 T ( k ) n·T(n)=n·(n-1)+2·\sum_{k=0}^{n-1}T(k) n⋅T(n)=n⋅(n−1)+2⋅∑k=0n−1T(k)
( n − 1 ) ⋅ T ( n − 1 ) = ( n − 2 ) ⋅ ( n − 1 ) + 2 ⋅ ∑ k = 0 n − 2 T ( k ) (n-1)·T(n-1)=(n-2)·(n-1)+2·\sum_{k=0}^{n-2}T(k) (n−1)⋅T(n−1)=(n−2)⋅(n−1)+2⋅∑k=0n−2T(k)
n ⋅ T ( n ) − ( n + 1 ) ⋅ T ( n − 1 ) = 2 ⋅ ( n − 1 ) n·T(n)-(n+1)·T(n-1)=2·(n-1) n⋅T(n)−(n+1)⋅T(n−1)=2⋅(n−1)
T ( n ) / ( n + 1 ) − T ( n − 1 ) / n = 4 / ( n + 1 ) − 2 / n T(n)/(n+1)-T(n-1)/n=4/(n+1)-2/n T(n)/(n+1)−T(n−1)/n=4/(n+1)−2/n
T ( n ) / ( n + 1 ) = T ( n ) / ( n + 1 ) − T ( 1 ) / 2 = 4 ⋅ ∑ k = 2 n 1 / ( k + 1 ) − 2 ⋅ ∑ k = 2 n 1 / k = 2 ⋅ ∑ k = 2 n + 1 1 / k + 2 / ( n + 1 ) − 4 ≈ 2 ⋅ ln n T(n)/(n+1)=T(n)/(n+1)-T(1)/2=4·\sum_{k=2}^n1/(k+1)-2·\sum_{k=2}^n1/k=2·\sum_{k=2}^{n+1}1/k+2/(n+1)-4≈2·\ln n T(n)/(n+1)=T(n)/(n+1)−T(1)/2=4⋅∑k=2n1/(k+1)−2⋅∑k=2n1/k=2⋅∑k=2n+11/k+2/(n+1)−4≈2⋅lnn
T ( n ) ≈ 2 ⋅ n ⋅ ln n = ( 2 ⋅ ln 2 ) ⋅ n log n ≈ 1.386 ⋅ n log n T(n)≈2·n·\ln n=(2·\ln 2)·n\log n≈1.386 ·n\log n T(n)≈2⋅n⋅lnn=(2⋅ln2)⋅nlogn≈1.386⋅nlogn
5.2 后向分析(Backward Analysis)
-
设经排序后得到的输出序列为: { a 0 , a 1 , . . . , a i , . . . , a j , . . . , a n − 1 } \{a_0,a_1,...,a_i,...,a_j,...,a_{n-1}\} {a0,a1,...,ai,...,aj,...,an−1}
-
这一输出与具体使用何种算法无关,故可使用Backward Analysis
-
比较操作的期望次数应为 T ( n ) = ∑ i = 0 n − 2 ∑ j = i + 1 n − 1 P r ( i , j ) T(n)=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}Pr(i,j) T(n)=∑i=0n−2∑j=i+1n−1Pr(i,j),亦即,每一对 < a i , a j > <a_i,a_j> <ai,aj>在排序过程中接受比较之概率的总和
-
quickSort的过程及结果,可理解为:按某种次序,将各元素逐个确认为pivot
-
若 k ∈ [ 0 , i ) ∪ ( j , n ) k∈[0,i)∪(j,n) k∈[0,i)∪(j,n),则 a k a_k ak早于或晚于 a i a_i ai和 a j a_j aj被确认,均与Pr(i,j)无关
-
实际上, < a i , a j > <a_i,a_j> <ai,aj>接受比较,当且仅当在 { a i , a i + 1 , . . . , a j − 1 , a j } \{a_i,a_{i+1},...,a_{j-1},a_j\} {ai,ai+1,...,aj−1,aj} 中, a i a_i ai或 a j a_j aj率先被确认
T ( n ) = ∑ i = 0 n − 2 ∑ j = i + 1 n − 1 P r ( i , j ) = ∑ j = 1 n − 1 ∑ i = 0 j − 1 P r ( i , j ) = s u m j = 1 n − 1 ∑ d = 0 j 2 / ( d + 1 ) ≈ ∑ j = 1 n − 1 2 ⋅ ( ln j − 1 ) ≤ 2 ⋅ n ln n T(n)=\sum_{i=0}^{n-2}\sum_{j=i+1}^{n-1}Pr(i,j)=\sum_{j=1}^{n-1}\sum_{i=0}^{j-1}Pr(i,j)=sum_{j=1}^{n-1}\sum_{d=0}^{j}2/(d+1)≈\sum_{j=1}^{n-1}2·(\ln j-1)≤2·n\ln n T(n)=∑i=0n−2∑j=i+1n−1Pr(i,j)=∑j=1n−1∑i=0j−1Pr(i,j)=sumj=1n−1∑d=0j2/(d+1)≈∑j=1n−12⋅(lnj−1)≤2⋅nlnn
5.3 对比
| #compare | #move (对实际性能影响更大) | in-placed | |
|---|---|---|---|
| Quicksort | 平均 O ( 1.386 ∗ n log n ) O(1.386*n\log n) O(1.386∗nlogn) 且高概率接近 | 平均不超过 O ( 1.386 ∗ n log n ) O(1.386*n\log n) O(1.386∗nlogn) 且实际更少 | ✓ |
| Mergesort | 严格 O ( 1.00 ∗ n log n ) O(1.00*n\log n) O(1.00∗nlogn) | 严格 O ( 1.00 ∗ n log n ) O(1.00*n\log n) O(1.00∗nlogn) 实际往往加倍 | ✗ |
6.快速划分:DUP版
6.1 重复元素
-
大量甚至全部元素重复时
- 轴点位置总是接近于lo
- 子序列的划分极度失衡
- 二分递归退化为线性递归
- 递归深度接近于O(n)
- 运行时间接近于O(n2)
-
移动lo和hi的过程中,同时比较相邻元素,若属于相邻的重复元素,则不再深入递归
-
但一般情况下,如此计算量反而增加,得不偿失
6.2 算法
template <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi)
swap( _elem[ lo ], _elem[ lo + rand() % ( hi – lo ) ] ); //随机交换
hi--; T pivot = _elem[ lo ]; //经以上交换,等效于随机选取候选轴点
while ( lo < hi ) { //从两端交替地向中间扫描,彼此靠拢
while ( lo < hi )
if ( pivot < _elem[ hi ] ) hi--; //向左拓展G,直至遇到不大于轴点者
else { _elem[ lo++ ] = _elem[ hi ]; break; } //将其归入L
while ( lo < hi )
if ( _elem[ lo ] < pivot ) lo++; //向右拓展L,直至遇到不小于轴点者
else { _elem[ hi-- ] = _elem[ lo ]; break; } //将其归入G
} //assert: lo == hi
_elem[ lo ] = pivot; return lo; //候选轴点归位;返回其秩
}
6.3 性能
-
可以正确地处理一般情况,同时复杂度并未实质增高
-
处理重复元素时
- lo和hi会交替移动
- 二者移动的距离大致相当,轴点最终被安置于(lo+hi)/2处
-
由LUG版的勤于拓展、懒于交换,转为懒于拓展、勤于交换
-
交换操作有所增加,更不稳定
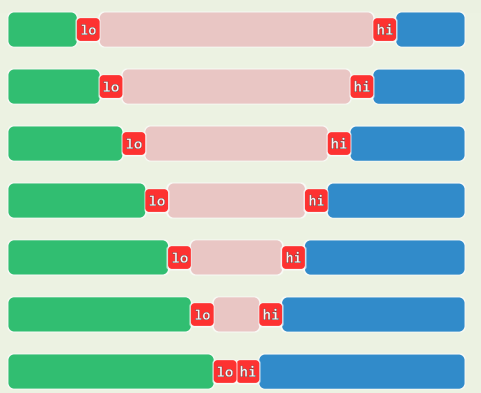
7.快速划分:LGU版
7.1 不变性
- S = [ l o , h i ) = [ l o ] + ( l o , m i ] + ( m i , k ) + [ k , h i ) = p i v o t + L + G + U , L < p i v o t < G S=[lo,hi)=[lo]+(lo,mi]+(mi,k)+[k,hi)=pivot+L+G+U,L<pivot<G S=[lo,hi)=[lo]+(lo,mi]+(mi,k)+[k,hi)=pivot+L+G+U,L<pivot<G

7.2 单调性
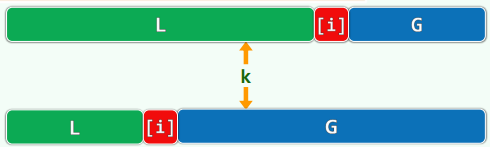
pivot <= S[ k ] ? k++ : swap( S[ ++mi ], S[ k++ ] )[k]不小于轴点 ? 直接 G 拓展 : G 滚动后移, L 拓展
7.3 算法
template <typename T> Rank Vector<T>::partition( Rank lo, Rank hi ) { //[lo, hi)
swap( _elem[ lo ], _elem[ lo + rand() % ( hi – lo ) ] ); //随机交换
T pivot = _elem[ lo ]; int mi = lo;
for ( Rank k = lo + 1; k < hi; k++ ) //自左向右考查每个[k]
if ( _elem[ k ] < pivot ) //若[k]小于轴点,则将其
swap( _elem[ ++mi ], _elem[ k ]); //与[mi]交换,L向右扩展
swap( _elem[ lo ], _elem[ mi ] ); //候选轴点归位(从而名副其实)
return mi; //返回轴点的秩
}
7.4 实例
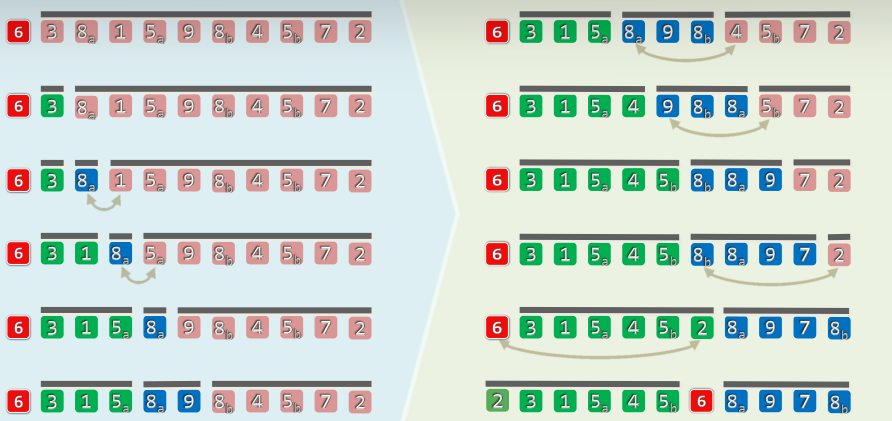
二、选取
1.众数
1.1 选取 + 中位数
- 中位数(median):长度为n的有序序列S中,元素 S [ ⌊ n / 2 ⌋ ] S[\lfloor n/2 \rfloor] S[⌊n/2⌋]称作中位数

- 中位数是k-选取的一个特例,也是其中难度最大者
1.2 众数(Majority)
- 无序向量中,若有一半以上元素同为m,则称之为众数
- 必要性:众数若存在,则亦必中位数
- 事实上,只要能够找出中位数,即不难验证它是否众数
template <typename T> bool majority( Vector<T> A, T & maj ) {
return majEleCheck( A, maj = median( A ) );
}
1.3 必要条件
- mode():众数若存在,则亦必频繁数
template <typename T> bool majority( Vector<T> A, T & maj ) {
return majEleCheck( A, maj = mode( A ) );
}
- 同样地,mode()算法难以兼顾时间、空间的高效
- 可行思路:借助更弱但计算成本更优的必要条件,选出唯一的候选者
template <typename T> bool majority( Vector<T> A, T & maj ) {
return majEleCheck( A, maj = majEleCandiate( A ) );
}
1.4 减而治之
- 若在向量A的前缀P(|P|为偶数)中,元素 x 出现的次数恰占半数,则A有众数,仅当对应的后缀 A − P 有众数m,且m就是 A 的众数

- 既然最终总要花费O(n)时间做验证,故而只需考虑A的确含有众数的两种情况:
- 若x = m,则在排除前缀 P 之后,m与其它元素在数量上的差距保持不变
- 若x ≠ m,则在排除前缀 P 之后,m与其它元素在数量上的差距不致缩小
1.5 算法
template <typename T> T majCandidate( Vector<T> A ) {
T maj;
for ( int c = 0, i = 0; i < A.size(); i++ )
if ( 0 == c ) {
maj = A[i]; c = 1;
} else maj == A[i] ? c++ : c--;
return maj;
}
2.中位数
2.1 归并向量的中位数
- 任给有序向量 S 1 S_1 S1和 S 2 S_2 S2,长度 n 1 n_1 n1和 n 2 n_2 n2
- 蛮力: 经归并得到有序向量S取 S [ ( n 1 + n 2 ) / 2 ] S[(n_1+n_2)/2] S[(n1+n2)/2]即是
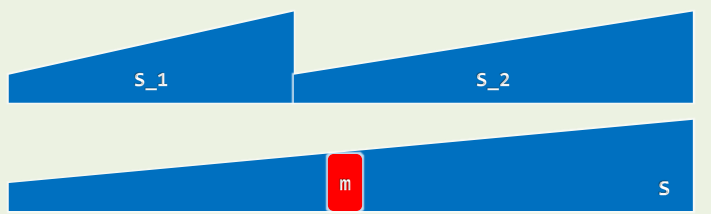
- 如此,共需 O ( n 1 + n 2 ) O(n_1+n_2) O(n1+n2)时间,但毕竟未能充分利用 S 1 S_1 S1和 S 2 S_2 S2的有序性
- 以下,先解决 n 1 = n 2 n_1=n_2 n1=n2的情况,依然采用减而治之策略
2.2 等长子向量

- 考查: m 1 = S 1 [ ⌊ n / 2 ⌋ ] m_1=S_1[\lfloor n/2 \rfloor] m1=S1[⌊n/2⌋]和 m 2 = S 2 [ ⌊ n / 2 ⌋ − 1 ] = S 2 [ ⌊ ( n − 1 ) / 2 ⌋ ] m_2=S_2[\lfloor n/2 \rfloor-1]=S_2[\lfloor (n-1)/2 \rfloor] m2=S2[⌊n/2⌋−1]=S2[⌊(n−1)/2⌋]
- 若 m 1 = m 2 m_1=m_2 m1=m2,则它们同为 S 1 S_1 S1、 S 2 S_2 S2和 S S S的中位数
- 若 m 1 < m 2 m_1<m_2 m1<m2,则n无论偶奇,必有: m e d i a n ( S 1 ∪ S 2 ) = , m e d i a n ( S 1 . s u f f i x ( ⌈ n / 2 ⌉ ) ∪ S 2 . p r e f i x ( ⌈ n / 2 ⌉ ) ) median(S_1∪S_2)=,median(S_1.suffix(\lceil n/2 \rceil)∪S_2.prefix(\lceil n/2 \rceil)) median(S1∪S2)=,median(S1.suffix(⌈n/2⌉)∪S2.prefix(⌈n/2⌉)),这意味着,如此减除(一半规模)之后,中位数不变
- m 1 > m 2 m_1>m_2 m1>m2时同理
template <typename T> //尾递归,可改写为迭代形式
T median( Vector<T> & S1, int lo1, Vector<T> & S2, int lo2, int n ) {
if ( n < 3 ) return trivialMedian( S1, lo1, n, S2, lo2, n ); //递归基
int mi1 = lo1 + n/2, mi2 = lo2 + (n - 1)/2; //长度减半
if ( S1[ mi1 ] < S2[ mi2 ] ) //取S1右半、S2左半
return median( S1, mi1, S2, lo2, n + lo1 - mi1 );
else if ( S1[ mi1 ] > S2[ mi2 ] ) //取S1左半、S2右半
return median( S1, lo1, S2, mi2, n + lo2 - mi2 );
else
return S1[ mi1 ];
}
2.3 任意子向量
template <typename T>
T median ( Vector<T> & S1, int lo1, int n1, Vector<T> & S2, int lo2, int n2 ) {
if ( n1 > n2 )
return median( S2, lo2, n2, S1, lo1, n1 ); //确保n1 <= n2
if ( n2 < 6 )
return trivialMedian( S1, lo1, n1, S2, lo2, n2 ); //递归基
if ( 2 * n1 < n2 )
return median( S1, lo1, n1, S2, lo2 + (n2-n1-1)/2, n1+2-(n2-n1)%2 );
int mi1 = lo1 + n1/2, mi2a = lo2 + (n1 - 1)/2, mi2b = lo2 + n2 - 1 - n1/2;
if ( S1[ mi1 ] > S2[ mi2b ] ) //取S1左半、S2右半
return median( S1, lo1, n1 / 2 + 1, S2, mi2a, n2 - (n1 - 1) / 2 );
else if ( S1[ mi1 ] < S2[ mi2a ] ) //取S1右半、S2左半
return median( S1, mi1, (n1 + 1) / 2, S2, lo2, n2 - n1 / 2 );
else //S1保留,S2左右同时缩短
return median( S1, lo1, n1, S2, mi2a, n2 - (n1 - 1) / 2 * 2 );
} //O( log(min(n1,n2)) )——可见,实际上等长版本才是难度最大的
3.快速选取(QuickSelect)
3.1 尝试:蛮力
- 对A排序( O ( n log n ) O(n\log n) O(nlogn)),从首元素开始,向后行进k步( O ( k ) = O ( n ) O(k) = O(n) O(k)=O(n))

3.2 尝试:堆(A)
- 将所有元素组织为小顶堆( O ( n ) O(n) O(n)),连续调用k+1次delMin() ( O ( k log n ) O(k\log n) O(klogn))

3.3 尝试:堆(B)
L = heapify( A[0, k] ) //任选 k+1 个元素,组织为大顶堆:O(k)
for each i in (k, n) //O(n - k)
L.insert( A[i] ) //O(logk)
L.delMax() //O(logk)
return L.getMax()
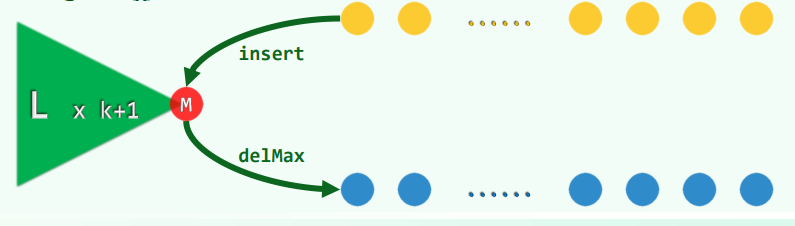
3.4 尝试:堆(C)
- 将输入任意划分为规模为k、n-k的子集,分别组织为大、小顶堆 //O(k + (n-k)) = O(n)
while ( m < M ) //O(min(k, n – k))
swap( m, M )
L.percolateDown() //O(logk)
G.percolateDown() //O(log(n - k))
return m = G.getMin()

3.5 下界与最优
- 所谓第k小,是相对于序列整体而言,所以在访问每个元素至少一次之前,绝无可能确定

3.6 算法
template <typename T> void quickSelect( Vector<T> & A, Rank k ) {
for ( Rank lo = 0, hi = A.size() - 1; lo < hi; ) {
Rank i = lo, j = hi; T pivot = A[lo]; //大胆猜测
while ( i < j ) { //小心求证:O(hi - lo + 1) = O(n)
while ( i < j && pivot <= A[j] ) j--; A[i] = A[j];
while ( i < j && A[i] <= pivot ) i++; A[j] = A[i];
} //assert: quit with i == j
A[i] = pivot;
if ( k <= i ) hi = i - 1;
if ( i <= k ) lo = i + 1;
} //A[k] is now a pivot
}
3.7 期望性能
- 记期望的比较次数为T(n)
- T(1)=0,T(2)=1,…
- 可以证明: T ( n ) = ( n − 1 ) + ( 1 / n ) ⋅ ∑ k = 0 n − 1 m a x { T ( k ) , T ( n − k − 1 ) } ≤ ( n − 1 ) + ( 2 / n ) ⋅ ∑ k = n / 2 n − 1 T ( k ) T(n)=(n-1)+(1/n)·\sum_{k=0}^{n-1}max\{T(k),T(n-k-1)\}≤(n-1)+(2/n)·\sum_{k=n/2}^{n-1}T(k) T(n)=(n−1)+(1/n)⋅∑k=0n−1max{T(k),T(n−k−1)}≤(n−1)+(2/n)⋅∑k=n/2n−1T(k)
- 事实上,不难验证: T ( n ) ≤ ( n − 1 ) + ( 2 / n ) ⋅ ∑ k = n / 2 n − 1 4 k ≤ ( n − 1 ) + 3 n ≤ 4 n T(n)≤(n-1)+(2/n)·\sum_{k=n/2}^{n-1}4k≤(n-1)+3n≤4n T(n)≤(n−1)+(2/n)⋅∑k=n/2n−14k≤(n−1)+3n≤4n
4.线性排序(LinearSelect)
4.1 linearSelect( A, n, k )
-
设Q为小常数
-
if ( n = |A| < Q ) return trivialSelect( A, n, k )递归基:序列长度|A| ≤ Q -> O ( 1 ) = O ( Q log Q ) O(1) = O(Q\log Q) O(1)=O(QlogQ) -
else divide A evenly into n/Q subsequences (each of size Q)子序列划分 -> O ( n ) O(n) O(n) -
Sort each subsequence and determine n/Q medians子序列各自排序,并找到中位数 -> O ( n ) = Q 2 ⋅ n / Q O(n)=Q^2·n/Q O(n)=Q2⋅n/Q -
Call linearSelect() to find M, median of the medians从n/Q个中位数中,递归地找到全局中位数 -> T ( n / Q ) T(n/Q) T(n/Q) -
Let L/E/G = { x</=/>M | x ∈ A }划分子集L/E/G,并分别计数 —— 一趟扫描足矣 -> O ( n ) O(n) O(n) -
if (k < |L|) return linearSelect(A, |L|, k)if (k < |L|+|E|) return Mreturn linearSelect(A+|L|+|E|, |G|, k-|L|-|E|)-> T(3n/4)
4.2 复杂度
-
T ( n ) = c ⋅ n + T ( n / Q ) + T ( 3 n / 4 ) T(n)=c·n+T(n/Q)+T(3n/4) T(n)=c⋅n+T(n/Q)+T(3n/4)
- m i n ( ∣ L ∣ , ∣ G ∣ ) + ∣ E ∣ ≥ n / 4 min(|L|,|G|)+|E|≥n/4 min(∣L∣,∣G∣)+∣E∣≥n/4
- m a x ( ∣ L ∣ , ∣ G ∣ ) ≤ 3 n / 4 max(|L|,|G|)≤3n/4 max(∣L∣,∣G∣)≤3n/4
-
当 1 / Q + 3 / 4 < 1 1/Q+3/4<1 1/Q+3/4<1时, T ( n ) = O ( n ) T(n)=O(n) T(n)=O(n)
三、希尔排序
1.框架+实例
1.1 希尔排序(Shellsort)
-
将整个序列视作一个矩阵,逐列各自排序
-
递减增量(diminishing increment)
- 由粗到细:重排矩阵,使其更窄,再次逐列排序(h-sorting/h-sorted)
- 逐步求精:如此往复,直至矩阵变成一列(1-sorting/1-sorted)
-
步长序列(step sequence):由各矩阵宽度逆向排列而成的序列
- H = { h 1 = 1 , h 2 , . . . , h k , . . . } H=\{h_1=1,h_2,...,h_k,...\} H={h1=1,h2,...,hk,...}
-
正确性:最后一次迭代,等同于全排序
- 1-sorted = ordered
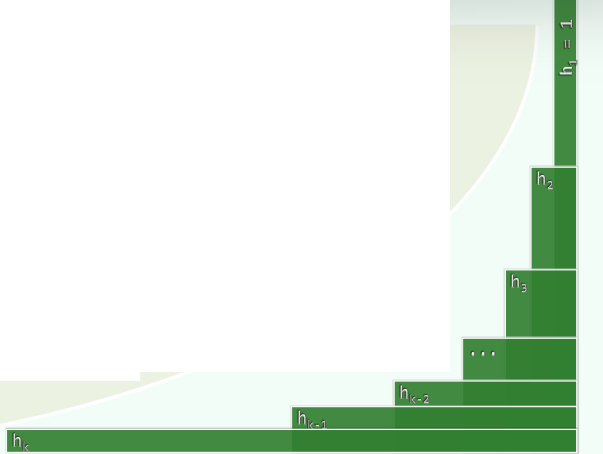
1.2 实例
- h 5 = 8 h_5=8 h5=8
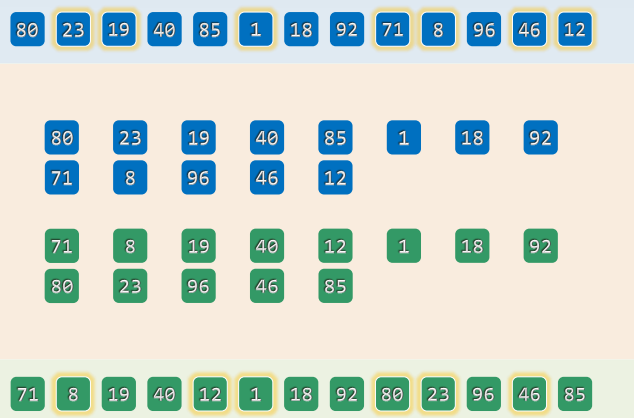
- h 4 = 5 h_4=5 h4=5
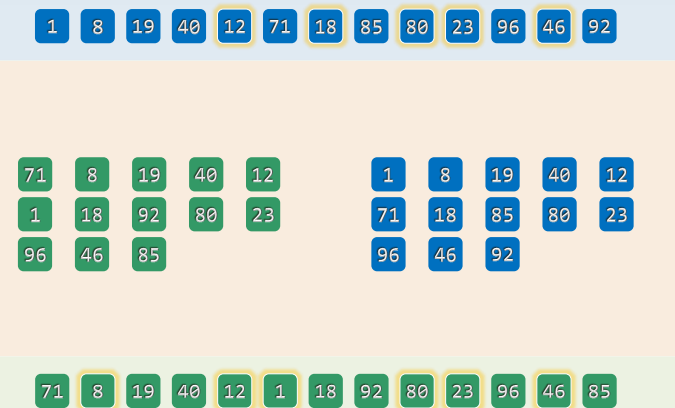
- h 3 = 3 h_3=3 h3=3

- h 2 = 2 h_2=2 h2=2

- h 1 = 1 h_1=1 h1=1

1.3 循秩访问
- 借助一维向量足以实现矩阵重排
- 在每步迭代中,若当前的矩阵宽度为,则 B [ i ] [ j ] = A [ i ⋅ h + j ] B[i][j]=A[i·h+j] B[i][j]=A[i⋅h+j]或 A [ k ] = B [ k / h ] [ k % h ] A[k]=B[k/h][k\%h] A[k]=B[k/h][k%h]
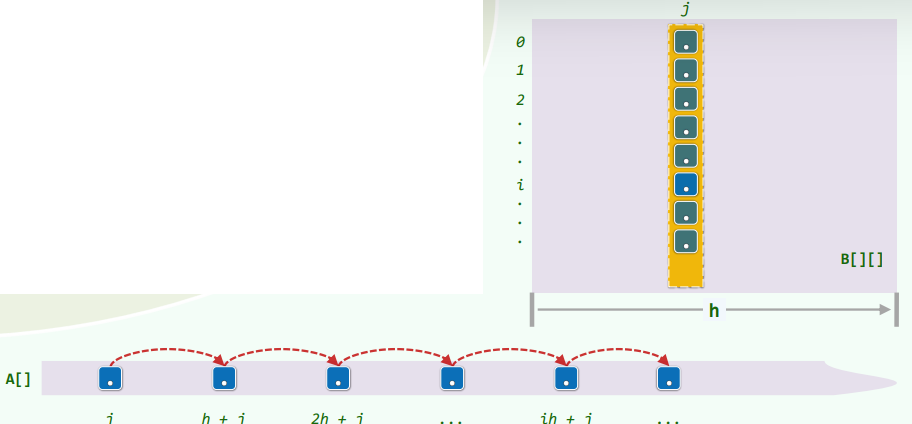
1.4 实现
template <typename T> void Vector<T>::shellSort( Rank lo, Rank hi ) {
// Using PS Sequence { 1, 3, 7, 15, 31, 63, 127, ..., 1073741823, ... }
for ( Rank d = 0x3FFFFFFF; 0 < d; d >>= 1 )
for ( Rank j = lo + d; j < hi; j++ ) { //for each j in [lo+d, hi)
T x = _elem[j]; Rank i = j - d;
while ( lo <= i && _elem[i] > x )
{ _elem[i + d] = _elem[i]; i -= d; }
_elem[i + d] = x; //insert [j] into its subsequence
}
} //0 <= lo < hi <= size <= 2^30





















 4491
4491











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








