【AutoCAD导出多线段为csv文件】【Abaqus拓扑仿真教程链接】【Transform .csv to .gcode】

Vaticann

已于 2025-03-30 14:50:09 修改

阅读量1.5k

点赞数 10

文章标签： lisp

于 2024-03-25 14:43:17 首次发布

本文链接：https://blog.csdn.net/Vaticann/article/details/137013196

版权

本文介绍了如何使用AutoCAD的AutoLisp和VisualLISP编辑器，编写一个LISP函数，自动从多线段提取坐标并保存为CSV文件，以简化3D打印路径规划过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

背景

【2024.3.25】我自己规划3D打印的路径时，使用AutoCAD进行具体的路径规划，但是苦于其多线段的坐标难以直接导出，摸索多日未得善终。
而后在ChatGPT4的建议下使用AutoCAD自带的代码语言AutoLisp，及其编辑器 Visual Lisp，实现选取多线段自动导出其所有坐标点为csv文件的功能。
具体代码由ChatGPT4生成，这里放在最后。
【2025.3.30】鉴于有学弟要重复我的工作，于是将这篇博文详实一些。

具体操作方式

这个操作方式可以实现点几下就能将Autocad里的多线段直接变成可以运行的Gcode文件。

将[线段]转成[多线段]然后合并，或者将多个[多线段]合并在一起
参考文章： AutoCAD多条线合并为一个整体即一条多段线方法
实际上就是使用在【命令行】输入”PE“，然后根据它的按钮指引就能完成线段合并。
使用的语言和编辑器 ：AutoLisp和Visual LISP 编辑器

编辑器打开的位置

autolisp代码片段

; 定义一个新的LISP函数
(defun c:GetPolylinePointsCSV ()
  ; 获取当前文档的名称
  (setq doc (vla-get-ActiveDocument (vlax-get-acad-object)))
  (setq filename (vla-get-Name doc))

  ; 提取文件名（无扩展名）
  (setq filetitle (vl-filename-base filename))

  ; 设置输出CSV文件的路径和文件名
  (setq csvpath (strcat filetitle "_polyline_points.csv"))

  ; 提示用户选择一个多项段
  (setq ss (ssget "_:S" '((0 . "LWPOLYLINE"))))
  (if ss
    (progn
      ; 如果用户成功选择了一个多项段
      (setq pline (ssname ss 0))
      ; 打开或创建一个CSV文件来保存坐标
      (setq f (open csvpath "w"))
      ; 写入CSV头部（如果需要）
      ; (write-line "X, Y" f)
      ; 初始化顶点索引
      (setq vtx 0)
      ; 循环遍历多项段的所有顶点
      (while (setq pt (vlax-curve-getPointAtParam pline vtx))
        ; 将每个顶点的坐标写入文件，格式为CSV
        (write-line (strcat (rtos (car pt) 2 2) ", " (rtos (cadr pt) 2 2)) f)
        ; 移至下一个顶点
        (setq vtx (+ vtx 1))
      )
      ; 关闭文件
      (close f)
      (princ (strcat "\n顶点坐标已成功保存至" csvpath "。"))
    )
    (princ "\n操作取消或未选择多项段。")
  )
  ; 清理并结束函数
  (princ)
)

; 在脚本末尾调用函数，使其在加载时自动执行
; 注意：这将立即执行函数，而不等待用户输入
(c:GetPolylinePointsCSV)

; 启动消息
(princ "\n'GetPolylinePointsCSV' 函数已自动运行。")
(princ)

编辑器中操作；

①在【文件】其中新建文件，将上述代码复制进去保存
②首次加载的话，点击下方图片上对应的按钮，然后回到cad绘图界面，接着选择多线段即可。
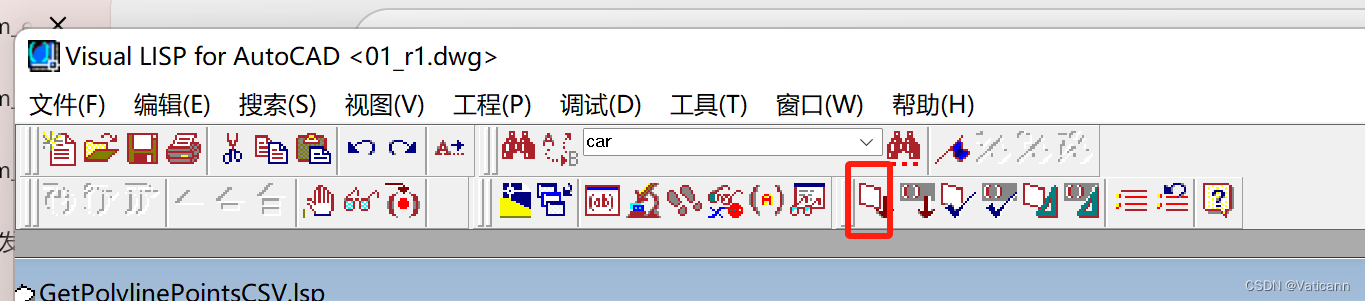
在这里插入图片描述
加载过的话，可以在【autocad的命令行】输入”GetPolylinePointsCSV“，这样就可以重复使用选取多线段的功能了，如下图所示：

③然后就会在dwg文件夹下生成一个csv文件。

可能要注意的事项；
如果不知道Lisp编辑器具体怎么使用，可以去B站上面查，几分钟就能学会。

Abaqus拓扑优化仿真链接

我是跟这个up主学习的：机械臂拓扑优化
这个up主的其他视频也有介绍其他限制条件（比如纯平面）的拓扑优化仿真
总之很酷！
拓扑优化结果实例

csv文件经由Python生成Gcode

其实我想过用autolisp一步到位，但是那个编程语言不太好使，还是用python转变成Gcode比较合适。
也考虑过用Python启动选取AutoCAD中的多线段直接导出想要的gcode文件，这样可以减少autolisp的步骤，但是python与autocad之间的连接一直不太稳定，这样反而更费功夫，于是不再使用这个方法。

import math
# import os
import pandas as pd
# import numpy as np

    # height：层高， X0 Y0 Z0：整体路径的对应坐标会加上这些值，F：打印的速度（开始和结束代码在本文件开头处修改），layer_num:层高，
    # symmetry: 0，每层打印完从初始点开始打印回去；1，每层打印完后从最后打印的一个点沿着原路径打印回去。    对称开启意味着你规划的路径同一层内首尾不相接
    # save_index: 给生成的gcode文件名上自动添加的后缀
    # Ex：每个点的E值 = E * Ex，所以Ex是调整E值的倍率因子
    # T：喷头（T0或T1），如只有一个喷头，请置空（T=“”）
def generate_path(height=0.35, X0=100.0, Y0=100.0, Z0=0.0,F=600, layer_num=6, symmetry=0,
                  filepath='', filename='', save_index='',Ex = 1.0, T=""):
    # 输入层高
    # height = 0.35
    # 输入中心坐标：X0,Y0
    # X0 = 100    # 大黑机,树脂打印头的初始点为（0,0），连续纤维打印头的初始点为（74，-28）
    # Y0 = 100    # 重置初始点，保证同一位置，两个打印头都能打印到。
    # Z0 = 0

    # symmetry = 1 # 是否对称
    # layer_num = 6  # 打印层数
    E = 0

    # 输入开始的默认代码
    original_code = f''';【【path{save_index}】】
{T}
M109 S220
M82 
G28
G90
G21
    
G92 
    
M106 S155
    '''
# 输入结束的默认代码
    final_code = '''
G1 Z30


M107
M104 S0
M140 S0
    '''

    speed = F
    X_location = 0  # X坐标所在列   第A、B、C列为 0，1，2
    Y_location = 1  # Y坐标所在列

    # 读取坐标,文件是csv类型
    data_firstlayer = pd.read_csv(filepath + filename + ".csv", header=None, index_col=None)
    len = data_firstlayer.shape[0]  # 一层的点的数量
    Gcode_txt = open(filepath + filename + save_index + "_2gcode.gcode", 'w')

    # 写入开始代码
    Gcode_txt.write(original_code)

    # 处理并写入坐标
    z_value = 0 + Z0  # 层高初始化
    # 打入初始点，初始点不参与循环

    # txt1 = "G1 X" + str(round(data_firstlayer.iat[2, X_location] + X0, 3)) + " Y" + str(
    #     round(data_firstlayer.iat[2, Y_location] + Y0, 3)) + ' E2.00' + '\n'
    # print(txt1)
    # Gcode_txt.write(txt1)

    # 设定初始点，并将初始点写入代码，初始点是有效打印线段的第一个点，方便计算E值
    xx_1 = float(data_firstlayer[X_location][0])
    yy_1 = float(data_firstlayer[Y_location][0])
    txt1 = f"""
G1 X{xx_1 + X0}  Y{yy_1 + Y0} Z3 F2500 \nG1 F{speed}\n"""

    # print(txt1)
    Gcode_txt.write(txt1)

    sym_open = 0
    data = data_firstlayer
    data_firstlayer_reversed = data_firstlayer[::-1]
    i = 0

    # 开始生成打印路径的gcode代码，并且写入
    while i != layer_num:  # 打印完最后一层就停止了

        i += 1
        z_value += height
        txt1 = "G1" + " Z" + str(z_value) + '\n'
        # print(txt1)
        Gcode_txt.write(txt1)

        if symmetry == 1:
            if sym_open == 0:
                data = data_firstlayer
                sym_open = 1
            else:
                data = data_firstlayer_reversed
                sym_open = 0

        for j in range(0, len):
            # 赋值点，方便后继调取
            xx = data.iat[j, X_location]
            yy = data.iat[j, Y_location]
            xx = float(xx)
            yy = float(yy)

            # 计算E值，E值是累积的，Ex是倍率
            Add_E = math.sqrt((xx - xx_1) * (xx - xx_1) + (yy - yy_1) * (yy - yy_1))
            E += Add_E * Ex

            # 生成Gcode指令行，并输入Gcode
            txt1 = f"G1 X{xx + X0} Y{yy + Y0} E{E} \n"

            # 保存本行的点，方便下一行计算E值
            xx_1 = float(data.iat[j, X_location])
            yy_1 = float(data.iat[j, Y_location])

            # 将gcode代码写入文本文件里
            # print(txt1)
            Gcode_txt.write(txt1)

    # 写入结束代码
    Gcode_txt.write(f'G1 Z{z_value}')
    # print(f'G1 Z{z_value}')
    Gcode_txt.write(final_code)
    Gcode_txt.close()

    print_time = (E/Ex)/F

    print(f" 【【{save_index}】】 Transformed successfully; \n final_Z: {z_value} height: {height}; \n layer_number: {layer_num}, symmetry: {symmetry}; "
          f"\n filename: {filename}; \n filepath: {filepath}; \n print_time: {print_time}min")
    print()

    return 1


if __name__ == "__main__":
    # excel文件请保存为csv类型
    # 路径和名称
    filepath = r"C:/Users/"
    filename = 'honeycomb3_polyline_points'

    # Xr = 0  # 树脂打印头的初始位置
    # Yr = 0
    # Xf = 0  # 纤维打印头的初始位置 # 73.5,24
    # Yf = 0


#根据需要生成不同的树脂
    # resin = generate_path(height=0.2, X0=100 + Xr, Y0=100 + Yr, Z0=0, layer_num=1, symmetry=0, filepath=filepath,
    #                       filename=filename, save_index='_resin', Ex=0.0665*2, T="T0")  # 生成树脂层路径
    fiber = generate_path(height=0.35, X0=100, Y0=100, Z0=0, F=300,layer_num=300, symmetry=0, filepath=filepath,
                          filename=filename, save_index='_fiber', Ex=1,T="T1")  # 生成连续纤维路径
    # little_black = generate_path(height=0.2, X0=100 , Y0=100 , Z0=0, F=300, layer_num=10, symmetry=0, filepath=filepath,
    #                       filename=filename, save_index="little_black")