傅里叶变换 - Fourier Transform

傅里叶级数

傅里叶在他的专著《热的解析理论》中提出，任何一个周期函数都可以表示为若干个正弦函数的和，即：

$$f(t)=a_0+\sum_{n=1}^{\infty}(a_ncos(n\omega t)+b_nsin(n\omega t))$$ 其中 $\omega=\dfrac{2\pi}{T}$， $T$为函数的周期。$a_n/b_n$和 $n$分别控制了正弦波的振幅与频率。这就是傅里叶级数的三角形式。
我们还可以用复指数形式1和积分2来表示傅里叶级数：
$$f(t)=\sum_{n=-\infty}^{\infty}F_ne^{in\omega t}$$ $$F_n=\frac{1}{T}\int_0^T f(t)e^{-in\omega t} dt$$ 其中 $F$就是周期函数$f$的 傅里叶级数(Fourier Series, FS)。
如果说$f$是某段信号在时域上的表现，$F$就是其在频域上的表现。傅里叶变换实现的就是从时域到频域的变换。

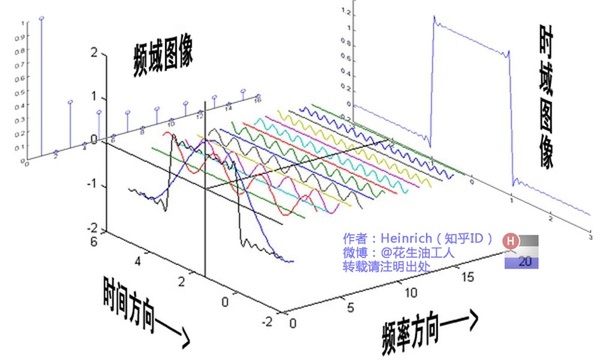
傅里叶变换

对于非周期函数，我们可以将其视为一个以$(-\infty,\infty)$为一个周期的周期函数。
经过数学推导，得到：

$$F(\omega)=\int_{-\infty}^\infty f(t)e^{-i\omega t} dt$$ $$f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)e^{i\omega t} d\omega$$ 这叫做 傅里叶变换(Fouier Transform, FT)及 傅里叶逆变换(IFT)。
注意，其结果都可能是复数。
这时， $F$不再是离散的级数，而是一个连续的函数了。
与傅里叶级数的比较：
- 傅里叶级数：周期信号，离散频率，频率分量的值
- 傅里叶变换：非周期信号，连续频率，频率分量的密度

卷积定理

卷积定理有两个：

$$FT[f_1(t)*f_2(t)]=FT[f_1(t)]\cdot FT[f_2(t)]$$ $$IFT[F_1(\omega)*F_2(\omega)]=\frac{1}{2\pi}IFT[F_1(\omega)]\cdot IFT[F_2(\omega)]$$ 分别称为 时域卷积定理和 频域卷积定理。

下面对时域卷积定理进行证明。

$$\begin{align} FT[f_1(t)*f_2(t)] &= FT[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau) d\tau] \\ &= \int_{-\infty}^\infty[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau) d\tau]e^{-i\omega t} dt \\ &= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t-\tau)e^{-i\omega t} dt]d\tau \\ &= \int_{-\infty}^\infty f_1(\tau)[\int_{-\infty}^\infty f_2(t)e^{-i\omega (t+\tau)} dt]d\tau \\ &= \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau}[\int_{-\infty}^\infty f_2(t)e^{-i\omega t} dt]d\tau \\ &= \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau}F_2(\omega) d\tau \\ &= F_2(\omega) \int_{-\infty}^\infty f_1(\tau)e^{-i\omega\tau} d\tau \\ &= F_1(\omega)F_2(\omega) \end{align}$$ 其实基本上就是直接展开啦。频域卷积定理的证明也是类似的。

可以观察到，在一个域上进行卷积，相当于在另一个域上进行点积。这启发我们用复杂度低的点积运算来代替复杂度高的卷积运算。

离散时间傅里叶变换

以上的内容都是针对连续信息/连续函数的。但是，计算机是无法存储连续的信息的，只能每隔时间$T$对信息进行采样。也就是说，计算机把连续的函数转化为了离散的序列。对于这样一个序列进行的傅里叶变换就称为离散时间傅里叶变换(Discrete Time Fouier Transform, DTFT)。

$$F(\omega)=\sum_{n=-\infty}^\infty f(nT)e^{-i\omega nT }$$ 我们其实是用离散的采样点$nT$代替了FT中连续的时间$t$。进一步，由于采样的结果本质上是一个序列，那么我们可以把序列中连续两项的间隔，也就是采样频率$T$看做单位“1”。我们用$x(n)$表示采样结果序列，那么有：

$$X(\omega)=\sum_{n=-\infty}^\infty x(n)e^{-i\omega n}$$ 事实上，这个将 $T$转化为“1”的过程，就是模拟信号转化为数字信号的过程。
其逆变换IDTFT的表达式为：
$$x(n)=\int_{-\pi}^\pi X(\omega)e^{i\omega n} d\omega$$

离散傅里叶变换

通过DTFT，我们已经能够处理离散的采样信号了。但由于采样结果序列依然是无限长的，计算机还是无法进行处理。从DTFT的式子中可以看出，$X(\omega)$是以$2\pi$为周期的，那么解决的方法很简单：我们只从时域$(0,2\pi)$上均匀地取$N$个点，用这$N$个点计算出频域上的$N$个点，这$N$个点就可以作为频域上的一个周期。

$$X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (k=0,1,2...,N-1)$$ 其中 $W_N=e^{-i\frac{2\pi}{N}}$，也就是n次单位根。
其实DFT就是将DTFT中的对 $\omega$积分替换为对 $\frac{2k\pi}{N}$求和 3。
这样，我们就得到了一个 $N$点信号到$N$点频域的离散变换，这个变换就叫做 离散傅里叶变换(Discrete Fourier Transform, DFT)。
其逆变换的表达式为：
$$x(n)=\frac{1}{N} \sum_{k=0}^{N-1}X(k)W_N^{-nk} \quad (n=0,1,2...,N-1)$$

FS, FT, DTFT, DFT的比较

变换	特点
傅里叶级数FS	周期信号，离散频率，频率分量的值
傅里叶变换FT	非周期信号，连续频率，频率分量的密度
离散时间傅里叶变换DTFT	非周期采样信号，连续频率，频率分量的密度
离散傅里叶变换DFT	有限长度非周期采样信号，离散频率，对于DTFT频谱频率分量的密度

快速傅里叶变换

朴素进行DFT的复杂度是$O(n^2)$，这可以从其表达式中看出。事实上我们有一种利用分治进行DFT的$O(nlogn)$算法，这就是常常被应用在OI中的快速傅里叶变换(Fast Fourier Transform, FFT)。
为了方便，以下若不做特殊说明，$N$均是$2$的整数次幂，这可以通过在原来的序列后补若干个$0$至有$2$的整数次幂项来实现。

$$\begin{align} X(k) &= \sum_{n=0}^{N-1}x(n)W_N^{nk} \\ &= \sum_{n=0,n+=2}^{N-2}x(n)W_N^{nk} + \sum_{n=1,n+=2}^{N-1}x(n)W_N^{nk} \\ &= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_N^{2nk} + \sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_N^{(2n+1)k} \\ &= \sum_{n=0}^{\frac{N}{2}-1}x(2n)W_{\frac{N}{2}}^{nk} + W_N\sum_{n=0}^{\frac{N}{2}-1}x(2n+1)W_{\frac{N}{2}}^{nk} \end{align}$$ 通过以上变形，原问题变成了两个规模减半的子问题。合并两个子问题的复杂度是 $O(1)$，分治层数为 $O(logn)$，所以计算一项的复杂度是 $O(logn)$，计算 $n$项的复杂度是$O(nlogn)$。

例题：多项式乘法

设$n$次多项式$f_1(x)=\sum_{i=0}^{n}a_ix^i$和$m$次多项式$f_2(x)=\sum_{i=0}^{m}b_ix^i$的积为$n+m$次多项式$f_3(x)=\sum_{i=0}^{n+m}c_ix^i$。给出序列$a,b$，求序列$c$。

容易知道$c_k=\sum_{i=0}^{k}a_ib_{k-i}$，事实上序列$c$就是序列$a$和序列$b$的离散卷积。
那么根据卷积定理，$c_k=IDFT[DFT[c_k]]=IDFT[DFT[a_k*b_k]]=IDFT[DFT[a_k]\cdot DFT[b_k]]$
所以我们只要将序列$a$和$b$DTFT到频域，点积后再IDTFT回时域，就可以得到序列$c$啦。

时间复杂度$O((n+m)log(n+m))$。

快速数论变换

在我们进行DTFT的过程中，使用的是复数。如果精度要求很高（比如求方案数），用复数来进行FFT就会出现误差。所以我们需要找到一个与复数单位根有相似性质的替代。
注意到FFT能够进行的根本因素就是复数单位根具有$W_N^2=W_{\frac{N}{2}}$这一性质。事实上，模意义域下的原根4就是复数单位根的一个很好的替代。
定义$W_N=g^{\frac{P-1}{N}}(mod \ P)$，则有：

$$X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad (mod \ P)$$ 这就是 快速数论变换(Number Theory Transform, NTT)。
进行NTT时，最常用的模数就是998244353，其原根 $g=3$。

---

1. $e^{i\theta}=cos\theta+isin\theta$ ↩
2. $\int_a^b f(x)dx$表示对$x\in(a,b)$的$f(x)$进行积分。 ↩
3. 把这个式子转化成类似DTFT的形式：
   $$X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk}=\sum_{n=0}^{N-1} x(n)e^{-i \frac{2k\pi}{N}n}$$ $\frac{2k\pi}{N}$代替的就是DTFT中$\omega$的位置。 ↩
4. 在模P意义下，如果有$g^{P-1}\equiv 1$，那么称$g$为$P$的原根。 ↩