【LeetCode解题报告】《算法基础010_因子分解和枚举》- Java

一、1492.n的第k个因子

1.题目

给你两个正整数 n 和 k 。
如果正整数 i 满足 n % i == 0 ，那么我们就说正整数 i 是整数 n 的因子。
考虑整数 n 的所有因子，将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ，请返回 -1 。
1 <= k <= n <= 1000

2.分析

看完题目，第一时间想的是：将找到的因子全都存到一个数组中，然后通过 k 来定位数组的下标获取因子。
刚开始觉得这个方法挺不错的，但是，再仔细想一下：

1. 这道题只求一个因子，同时 n 的范围又小。
2. 每个因子前后之间并没有太复杂的联系。
3. 那我还用个锤子的数组！

思路：

1. 定义计数的变量 int count = 0;
2. 遍历1 到 n，每遍历到一个能整除 n 的数，count 就自增。
3. 当计数变量 count 和 k 相等时，说明当前遍历到的数就是第 k 个因子。

3.代码

    public int kthFactor(int n, int k) {
        int i,count = 0;
        for (i = 1;i <= n;i++){
            if (n % i == 0){
                count++;
                if (count == k){
                    return i;
                }
            }
        }
        return -1;
    }

二、1362.最接近的质数

1.题目

1362.最接近的质数

给你一个整数 num，请你找出同时满足下面全部要求的两个整数：
两数乘积等于 num + 1 或 num + 2
以绝对差进行度量，两数大小最接近
你可以按任意顺序返回这两个整数。
1 <= num <= 10⁹

2.分析

方法一、

1. 得到 num +1 和 +2 后的两个数，分别从 Math.sqrt(num+1) 和 Math.sqrt(num+2)
   开始遍历，直到第一个能整除的数，然后比较两者的绝对值，小的那一组存入数组返回。

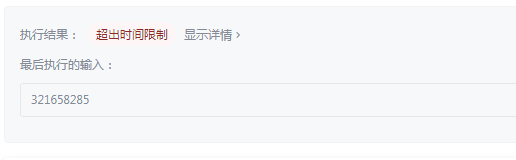
题目看似简单，但是，在运行到 num = 321658285 时，超出时间限制了。。。。

后来，在方法一的基础上，进行了改进：

方法二、

1. 首先，逻辑是没有问题的，从 num + 1 和 num + 2 的平方根开始遍历，第一个整除的数对就是绝对差最小的。
2. 把内层的for循环换成 while(true) 死循环，取到第一个整除的数对就跳出循环，这样不用像for循环那样每次都判断自增后的值是否超出范围，可以在数据比较大的时候节省比较多的时间。

方法三、

看题解发现了一个更高效的方法，值得学习：

1. 从较大数 num + 2 的平方根开始遍历，找最接近的小因子。
2. (num + 2) % i == 1，也就是 (num + 1) % i == 0，所以 (num + 2) % i = 0或1时都满足条件
3. 当余数为0时，大因子为 (num + 2) / i；
4. 当余数为1时，大因子为 (num + 1) / i，同时，当 i 不为 1 时，有 (num + 1) / i == (num + 2) / i
   因为(num + 2) % i == 1 的情况，在求另一个因子 (num + 2) / i 时，虽然不能整除，但小数部分会在强转成 int 类型时忽略掉，所以结果等同于 (num + 1) / i
5. 这里需要考虑一种特殊情况，当 num = 1 时，即 num + 1 和 num + 2 分别为 2 和 3，由于两个数都是质数，所以最后都会除到1，这时候应该返回 1 和 num + 1 ，绝对差最小（即：[1,2]）
6. Q：为什么num = 1才考虑特殊情况，num 大于1之后就没有这种情况了吗？
   A：是的，因为 2 是唯一一个偶数的质数，其他的质数都是奇数。当num > 1，即使其中一个数是质数，也必定会有另一个数是偶数，所以至少也会返回 [ 2 , num + 2 / i ]

3.代码

方法一、（超出时间限制）

    public int[] closestDivisors(int num) {
        int[] n = new int[2];
        int i,j;
        int abs = -1;
        for (i = num + 1;i <= num + 2;i++){
            for (j = (int) (Math.sqrt(i) + 1e-6);j >= 1;j--){
                //整除的第一对因子，就是最接近的
                if (i % j == 0){
                    if (abs == -1 || Math.abs(i / j - j) < abs){
                        abs = Math.abs(i / j - j);
                        n[0] = j;
                        n[1] = i / j;
                        break;
                    }
                }
            }
        }
        return n;
    }

方法二、

    public int[] closestDivisors(int num) {
        int[] n = new int[2];
        int i,j;
        int abs = -1;
        for (i = num + 1;i <= num + 2;i++){
            j = (int) (Math.sqrt(i));
            while (true){
                if (i % j == 0){
                    if (abs == -1 || Math.abs(i / j - j) < abs){
                        abs = Math.abs(i / j - j);
                        n[0] = j;
                        n[1] = i / j;
                    }
                    break;
                } else {
                    j--;
                }
            }
        }
        return n;
    }

方法三、

    public int[] closestDivisors(int num) {
        int divisor = num == 1 ? num + 1 : num + 2;
        int i = (int) Math.sqrt(divisor);
        while (divisor % i > 1) {
            i--;
        }
        return new int[]{i, divisor / i};
    }

三、1808.好因子的最大数目

1.题目

1808.好因子的最大数目

给你一个正整数 primeFactors 。你需要构造一个正整数 n ，它满足以下条件：
（1）n 质因数（质因数需要考虑重复的情况）的数目 不超过 primeFactors 个。
（2）n 好因子的数目最大化。如果 n 的一个因子可以被 n 的每一个质因数整除，我们称这个因子是 好因子 。比方说，如果 n = 12 ，那么它的质因数为 [2,2,3] ，那么 6 和 12 是好因子，但 3 和 4 不是。

请你返回 n 的好因子的数目。由于答案可能会很大，请返回答案对 10⁹ + 7 取余 的结果。
请注意，一个质数的定义是大于 1 ，且不能被分解为两个小于该数的自然数相乘。一个数 n 的质因子
是将 n 分解为若干个质因子，且它们的乘积为 n 。
1 <= primeFactors <= 10⁹

2.分析

这道题说实话没有思路，看了题解后自己再理解：

1. 根据题意，设要构造的数为num，其质因数数目不超过primeFactors。
2. 不妨将num进行质因数分解：num = a1^k1×a2^k2×…×an^kn，其中a1,a2,…,an是不同的质数，k1+k2+…+kn <= primeFactors
3. num的好因子，要能被所有a1,a2,a3,…,an整除，因为a1,…,an互质，因此，好因子必须含有a1×a2…×an作为因数。
4. 显然，好因子的个数 k = k1×k2×…×kn。 题目是要求k最大化，并返回k。

现在问题转化为：

正整数 k1+k2+…+kn <= primeFactors（1<=primeFactors<=10^9）
求k1×k2×…×kn的最大值。
很显然，为了让k1k2…*kn尽可能大，k1+k2+…+kn自身先要尽可能的大，最大到输入的primeFactors。

• 这就是 [343. 整数拆分] 原题，将一个正整数拆分成多个正整数的和，要求拆出来的数的乘积最大。
  之前是说尽可能拆成3，即让primeFactors=3+3+3…+3+(0/1/2)。

注意细节：

• 如果拆出来余数是1：将最后一个3和1合并为4，拆成2+2，这样能得到更大的乘积4。（详见代码实现）
• 注意primeFactors<=3时，特殊处理。

为何是3？

• 解释1：

根据均值不等式

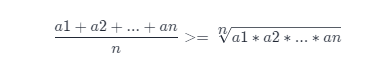
上式仅当a1=a2=…=an时取得等号。

对一个和尽可能进行等值拆分，拆分出来的数乘积最大。

如果对n进行x份等值拆分，得到的乘积

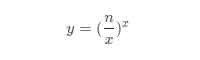
上式当x=e(2.71828…)时，取得最大值。如果只算整数，最接近e的整数3会使得y最大。

• 解释2：

Q：为什么不拆分成更小的2+2+…，或者更大的4+4+…呢？
A：拆成1肯定不行，最后得到的乘积是1。

• 关于2，可以举个例子：6=2+2+2=3+3，显然3×3比2×2×2更大。
• 关于4及以上的情况，如果x>=4，那么还可将x继续拆为 x-2 + 2，因为(x-2)×2>=x，也就是说将大于等于4的x继续拆能得到更大的乘积。

3.代码

	public int maxNiceDivisors(int n) {
	    int N = 10_0000_0007;
	    if (n <= 3) {
	        return n;
	    }
	    int a = n / 3, b = n % 3;
	    if (b == 1) {
	        return (int) (quickPow(3, a - 1, N) * 4 % N);
	    } else if (b == 2) {
	        return (int) (quickPow(3, a, N) * 2 % N);
	    } else {
	        return (int) quickPow(3, a, N);
	    }
	}

	/**
	 * 快速求幂：
	 * p^q，计算中防止溢出，对MOD求余
	 */
	public long quickPow(int p, int q, int MOD) {
	    long ans = 1L;
	    long base = p;
	    while (q != 0) {
	        if ((q & 1) == 1) {
	            ans = ans * base % MOD;
	        }
	        base = base * base % MOD;
	        q >>>= 1;
	    }
	    return ans;
	}