第二章补充：定积分（B站：一高数）_定积分」一课通!概念+性质一站式到位!-CSDN博客

本文链接：https://blog.csdn.net/Vincent_Zhang233/article/details/144174503

视频1：「定积分」一课通！概念+性质一站式到位！

一、概念导入与深度理解

在这个部分，我们将像数学家一样，从实际问题中探索出定积分的严格定义，同时读懂和欣赏伟大的定积分符号。

首先，我们像数学家一样，从实际问题中把定积分的定义设想出来。

如下图👇，作为一名老司机，你的车速曲线是随意变化的，请问，该如何计算你开过的路程呢？也就是如何计算蓝色不规则图形的面积呢？

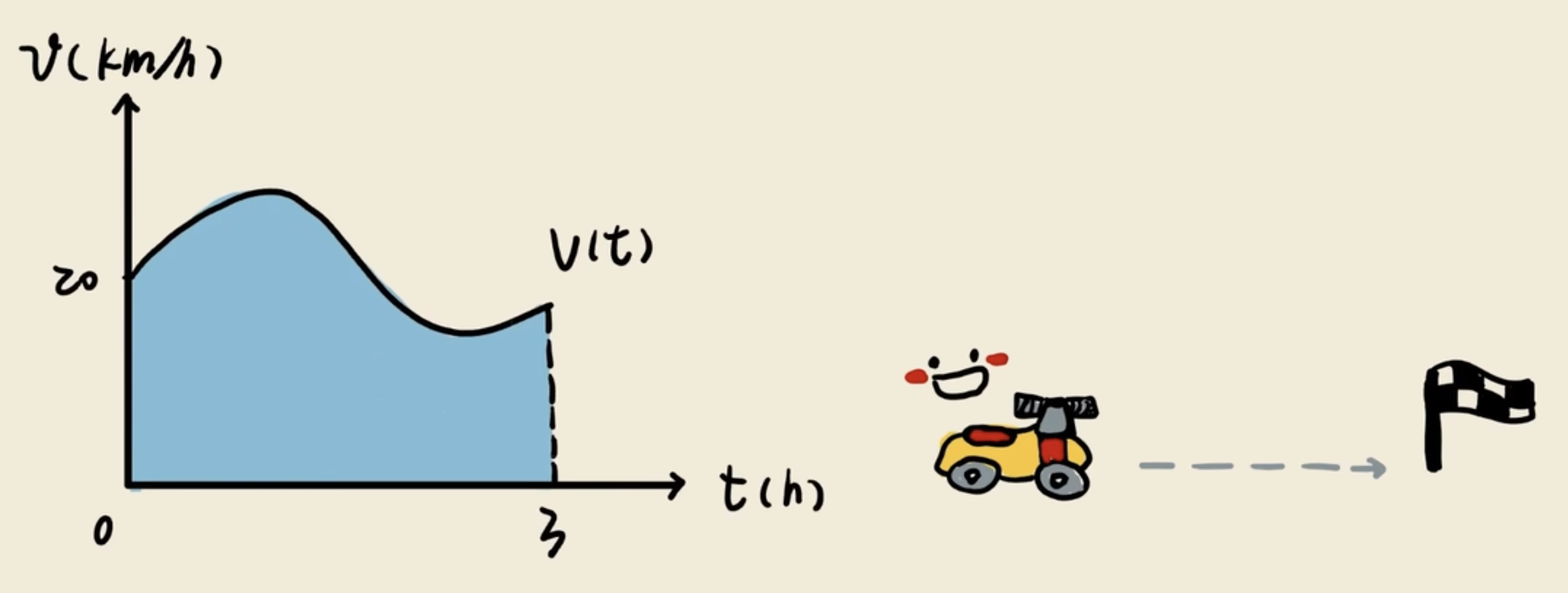
如果我把总时长随意拆分成5段，每一段都取速度的中间值作为高度画矩形。如下图👇

当然，这些小矩形越多，分割越细，近似效果就越好。比如，我们分割出n个小区间，每个小区间上我们都取某一点的函数值 $v(\xi)$ 作为它的高度，这样 $v(\xi_{i})\Delta t_{i}$ 就可以得到第 $i$ 个小矩形的面积。再把从1到n所有小矩形面积求和，就可以约定于曲线下方蓝色部分的面积 $S$ 了，而这个求和，就是传说中的“黎曼和”。如下图所示👇

如果想让这个“逼近”变得更加精确，我们再加一点点极限思维，让每一个区间的长度都很小很小，即最大区间长度趋近于0（ $\lambda \rightarrow 0$ ），再求刚才黎曼和的极限，这个极限值就应当是我们要求的面积 $S$ ，也就是总路程。即： $S=\lim_{\lambda \rightarrow 0}\sum_{i=1}^{n}v(\xi _{i})\Delta t_{i}$

巧了，数学家们也是这个想法，并且最终抽象出了定积分的严格定义。这个定义非常的长，你可以把它拆解为4个动作。如下图👇

用元素法（微元法）理解定积分符号👇这是用微分解决实际问题的核心方法

定积分能让我们在密度不均匀的情况下依然能游刃有余地求出质量，这就是它的厉害之处。把定积分利用在科学和生活的方方面面，就能解开宇宙变化之谜，甚至预测未来。

注：一般国内的考试和考研都默认面积是大于等于0的，但是由于上图的定积分 $S_{2}$ 应该是小于0的，所以就用 $-S_{2}$ 使其符合实际情况。

二、可积函数

总结：

学完上面的内容后，在本部分，我们将要知道哪些函数是可积的，并解决一类重难点问题——用定积分求n项和数列极限。

三、n项和数列极限

略

四、定积分的基本性质（5个）

最后，在本部分我们将串讲定积分重要性质，包括估值、比大小、中值定理等等。实现从0基础小白，到理解定积分的升级。

视频2：牛莱公式的发现之旅？变限积分+微积分基本定理！

原视频：牛莱公式的发现之旅？变限积分+微积分基本定理！_哔哩哔哩_bilibili

在这个视频中，我们要讲整个微积分当中最重要的一个公式——牛顿-莱布尼茨公式（也叫微积分基本定理）。我们将继续探索定积分中的一些隐藏关系，从而引入“变现积分”这个重要概念，从而给出微积分基本定理（也就是牛顿-莱布尼茨公式），正式完成定积分计算的入门

一、探索探索微分积分的关系

如上图所示👆，在上次视频中，我们用定积分分割、近似、求和、取极限的定义，硬核算出了 $x^{2}$ 在[0,1]上的积分。但是我们也发现了，如果题目再复杂一些，无论是从求和公式，还是从整套极限的计算都会非常复杂。所以我们急需一套不做分割近似求和取极限也能求定积分的方法。

如上图👆，当物体沿着某个方向做变速直线运动的时候，我想求 $t_{1}$ 到 $t_{2}$ 时刻走的总路程。

我们把这个事情推广到更加一般化的情况：在 $a$ 到 $b$ 上对函数 $f(x)$ 积分，结果就等于它的原函数（逆向求导） $F(b)-F(a)$

二、变限积分引入

由上图可知，其实 $f(x)$ 就是面积的导数，而且我们也能直观感觉到，当 $f(x)$ 的值大时，面积增加得也大（ $f(x)$ 那么高，面积增加的也就多）

下面，我们正式来看理论部分的总结：

牛顿-布莱尼次公式就是从下面👇这个“变限积分”这里被引出来的

上图中👆，由于由于微分中值定理， $\xi$ 是位于区间 $[x,x+\Delta x]$ 上的一个值，使 $f(\xi )\Delta x=\int_{x}^{x+\Delta x}f(x)dx=\Delta \Phi ' (x)$ 成立。当 $\Delta x\rightarrow 0$ 时，区间 $[x,x+\Delta x]$ 无限接近于 $x$ ，所以 $\xi \rightarrow x$ ，即： $f(\xi )=f(x)$

在知道变限积分求导的结论之后，我们想到一件事情👇：

那么下面我们就正式练一个例题：

其实铺垫到这里，对我们推出微积分基本定理已经够用了。但是考虑到大家考试要解决的题型，我们再围绕变限积分开两个支线任务👇（变限积分求导题型、变限积分的天然连续性）。

三、变限积分求导题型

略

四、变限积分F(x)的天然连续性

上面这个证明过程就比较硬核了，是给好奇宝宝看的，就是那些想知道为什么可积必连续的人看的。同时，也提供了一些证明题的方向。

五、牛顿-莱布尼茨公式

下面，我们回到主线任务——微积分基本定理（牛顿-莱布尼茨公式）

从名字来看，它非常基本，它是整个定积分乃至整个微积分这个数学学科的最最核心的公式之一。其实就是我们最开始发现的那个规律：如果一个连续的函数 $f(x)$ 在 $[a,b]$ 区间上有一个原函数 $F(x)$ （当然这个原函数肯定是有的），那么你对 $f(x)$ 在 $[a,b]$ 上定积分就等于原函数 $F(b)-F(a)$