朴素贝叶斯分类算法
一 算法基本内容
朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类算法。对于给定的数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布。然后基于此模型,对给定的输入,利用贝叶斯定理求出后验概率最大。
朴素贝叶斯分类属于生成模型,生成模型由数据学习联合概率分布P(X,Y),然后求出条件概率分布P(Y/X)作为预测的模型,即生成模型:
P(Y/X)=P(X,Y)/P(X)
最小化分类错误的贝叶斯最优分类器为
h(x)= arg max P(c/x)
对于生成模型,必然考虑:
P(c/x) = P(x,c)/P(x)
基于朴素贝叶斯定理,P(c/x)可以写为:
P(c/x) = P(c)P(x/c)/P(x)
其中,P(c)是先验概率,P(x/c)是样本x相对于类标记c的类条件概率,或者称为似然。对于参数C,所有的想都是相同的,因此
分类取值: C=arg max P(c)P(x/c)
朴素贝叶斯算法流程:
(1)根据数据计算先验概率与条件概率
(2)计算后验概率
(3)求出最大的后验概率估计
对类条件概率P(x/c)来说,由于它涉及关于x所有属性的联合概率,直接根据样本出现的频率来估计将会遇到更严重的困难。例如,假设样本的d个属性都是二值的,则样本空间将有2^d(指数形式)种可能的取值,在现实应用中,这个值远远大于训练样本数吗,也就是说,很多样本取值在训练集中根本没有出现,直接使用频率来估计P(x/c)显然不可行,因为未被观测到与出现概率为零通常是不同的。
解决这一问题,在估计概率值时,通常要进行平滑,常用“拉普拉斯修正”。拉普拉斯修正就是保证分子分母不为0.即相当于保证所有特征取值都出现过。
朴素贝叶斯的主要优点有:
1)朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
3)对缺失数据不太敏感,算法也比较简单,常用于文本分类。
朴素贝叶斯的主要缺点有:
1) 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2)需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3)由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
4)对输入数据的表达形式很敏感。即适用于标称性数据。
(1)极大似然估计:最大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。简单而言,假设我们要统计全国人口的身高,首先假设这个身高服从服从正态分布,但是该分布的均值与方差未知。我们没有人力与物力去统计全国每个人的身高,但是可以通过采样,获取部分人的身高,然后通过最大似然估计来获取上述假设中的正态分布的均值与方差。
二 算法拓展
(1) 最大似然估计中采样需满足一个很重要的假设,就是所有的采样都是独立同分布的。
求解似然函数的过程。
(a)写出似然函数;
(b)对似然函数取对数,并整理;
(c)求导数 ;
(d)解似然方程
(2)最大后验概率估计:最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似,但是最大的不同时,最大后验估计的融入了要估计量的先验分布在其中。故最大后验估计可以看做规则化的最大似然估计。
具体两种估计形式推导如下:








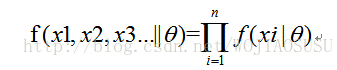
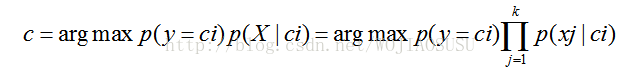

















 5377
5377

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








