在学习随机梯度下降法时,首先再了解一下几个简单的知识点。
(1) 知识点1:可导,可微,连续
对于多元函数,如果每个偏导都存在且连续(单单存在偏导数是不够的一定也要连续)那么就可以得到该函数可微,可微就可以推出该函数连续。而连续不可以反推。在一元函数中,可导和可微是等价的。可导必连续,连续不一定可导。
(2) 知识点2:方向导数与梯度
偏导数反映的是函数沿坐标轴方向的变化率。但是许多物理现象表明,只考虑沿坐标轴方向的变化率是不够的。于是引入函数沿某一方向的变化率,即方向导数。如果函数在某点可微,那么函数在该点沿任一方向L的方向导数存在。
举个例子说明一下:
已知F(x,y,z)=xy+yz+zx,求F在点(1,1,2)沿方向l的方向导数,其中l的方向角分别为60,45,60
解析:l的单位方向向量为e=(cos60,cos45,cos60)
因为函数可微分,且Fx(1,1,2)=(y+z)=3 Fy(1,1,2)=(x+z)=3 Fz(1,1,2)=(y+x)=2
那么方向导数为:3*cos60+3*cos45+2*cos60
可以发现最后方向导数出来的是一个具体的数值,而不是一个向量。这一点非常重要。
那么方向导数的作用呢?
(a)方向导数正负决定了函数升降;
(b)升降速度的快慢由方向导数绝对值大小来决定,绝对值越大升降速度越大;
设函数F(x,y)在平面区域D内具有一阶连续偏导数,则对于每一点P0(X0,Y0),都可以定出一个向量:Fx(X0,Y0)*i+Fy(X0,Y0)*j
这个向量称为函数F(x,y)在某点的梯度。即梯度是一个向量。
还是原先的例子:已知F(x,y,z)=xy+yz+zx,求F在点(1,1,2)的梯度。
解析:梯度为(3,3,2)
梯度与方向导数的关系:
方向导数=Fx(X0,Y0)*cosa+Fy(Xo,Y0)*cosb = grad F(X0,Y0)*e = |gradF(X0,Y0)|*cosA
通过公式可以可以发现:当方向导数沿梯度方向时,方向导数取得最大值。最大值就是梯度的模。
(3) 知识点3:线性规划的一半形式
如果目标函数是求最大值,那么可以变成:min –f.
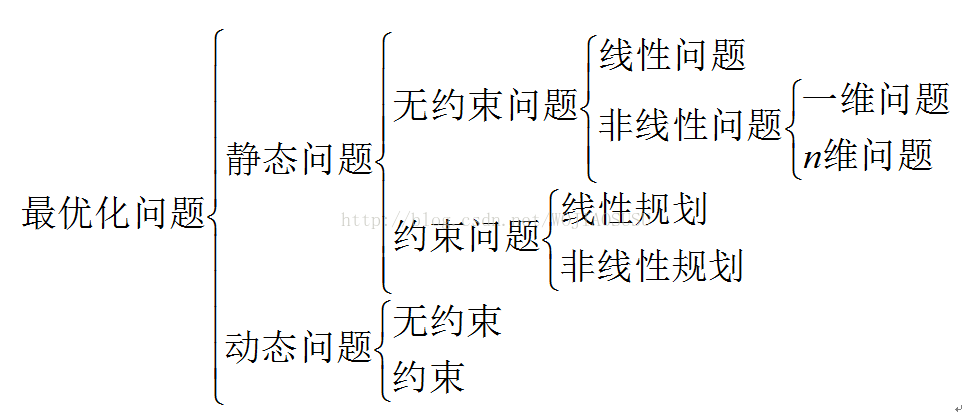
优化问题分类:
(1) 按照有没有约束条件,可以分为无约束优化与约束优化问题。
(2) 按照函数类型,可以分为
(a) 线性规划:目标与约束都是线性函数。
(b) 二次规划:目标是二次函数,约束是线性函数
(c) 非线性规划:目标函数不是一次、二次函数,或者约束条件不是线性函数
(4)知识点4:梯度相关性质
如果函数在某点可微,那么梯度存在。对多元函数来说,只要在某点偏导数都存在即可。如果偏导数存在且连续,那么梯度也是连续的。此时梯度具有以下两条性质:
(1) 函数在某点的梯度不为零,则必与过该点的等值面垂直
(2) 梯度方向是函数具有最大变化率的方向。
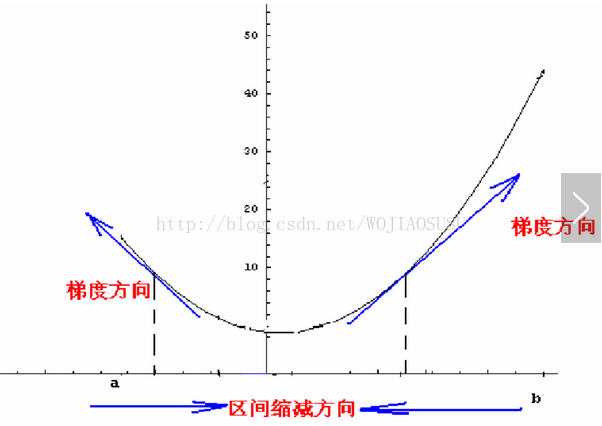
梯度最重要的性质:
梯度方向即为函数的最速上升方向。负梯度方向即为最速下降方向。下图可以清晰的说明这条性质。
几个常用的梯度方向:
(5)知识点5:海塞矩阵
基础点讲了之后,接下来就是梯度下降法
梯度下降法或者最速下降法是求解无约束条件的一种常用的方法。
算法思想就是:梯度下降法是一种迭代算法,选取适当的初值之后,不断迭代,进行目标函数的最小化,直到收敛,由于负梯度方向是下降最快的方向,在迭代的每一步,以负梯度方向更新x的值,从而减少函数值的目的。
特点:
(1) 因为使用了精确一维搜索,所以相邻两次的迭代方向互相垂直。
(2) 因为使用了精确以为搜索,所以最速下降法收敛速度慢。
最速下降法的优缺点:
优点:理论明确,结构简单,每次计算量少,所需的存储量少,对初始点要求不严格。
缺点:收敛速度慢。一般情况下,不保证最优解,只有目标函数是凸函数时,才会保证最优解。
改进:
(1) 选择不同的初始点
(2) 采用不精确的一维搜索。有时为了减少计算量,直接固定步长
(3) 采用加速梯度法。
随机梯度下降法主要原理(手写版):








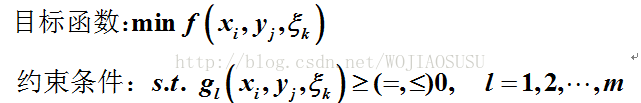

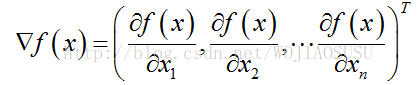
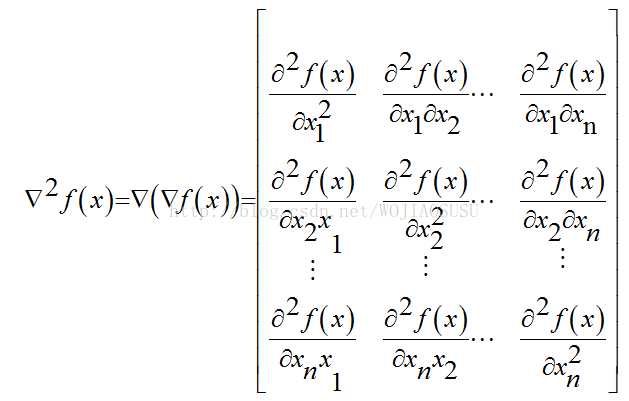
















 1051
1051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








