关于OCSVM与SVDD的理解

文章参考链接：
关于OCSVM
1、通俗易懂的理解：什么是一类支持向量机（one class SVM），是指分两类的支持向量机吗？
2、异常检测（一）——OneClassSVM
3、无监督︱异常、离群点检测 一分类——OneClassSVM
关于SVDD
1、SVDD(Support Vector Domain Description) 支持向量数据域描述

两者的比较
1、SVDD和OCSVM的比较
2、One Class SVM, SVDD（Support Vector Domain Description）

一、OCSVM

1、原理引入
OCSVM（one class support vector machine）即单类支持向量机， 该模型将数据样本通过核函数映射到高维特征空间，使其具有更良好的聚集性，在特征空间中求解一个最优超平面实现目标数据与坐标原点的最大分离，如图1：

坐标原点被假设为唯一的一个异常样本，最优超平面与坐标原点最大距离为, 并允许少部分样本在坐标原点与分界面之间，与分类超平面的距离为。

2、通俗理解单分类与多分类
我们知道，classification问题一般都是2类及2类以上的，典型的2类问题比如识别一封邮件是不是垃圾邮件，这里就只有2类，“是”或者“不是”，典型的多类classification问题比如说人脸识别，每个人对应的脸就是一个类，然后把待识别的脸分到对应的类去。

那么one class classification是什么呢？它只有一个类，然后识别的结果就是：“是”或者“不是”这个类。咦？听起来和2类classification问题貌似几乎一样，它们有什么区别呢？区别在于，在2类classification问题中，training set中有2个类，通常称为正例和负例，例如对于垃圾邮件识别问题，正例就是垃圾邮件，负例就是正常邮件，而在one class classification中，就只有一个类。听着好像有点神奇，什么情况下会出现training set中只有一个类的情况？一般是在的确手头上只有一类样本数据的情况下，或者是别的类数据不好确定的情况下，什么叫不好确定呢？举个例子，比如现在有一堆某产品的历史销售数据，记录着买该产品的用户的各种信息（这些信息在特征提取时会用到），然后还有些没买过该产品的用户的数据，想通过2类classification预测他们是否会买该产品，也就是弄2个类，一类是“买”，另一类是“不买”。这时候问题就来了，如果把买了该产品的用户看成正例，没买该产品的用户看成负例，就会出现（1）已经买了的用户，可以明确知道他已经买了，而没买的用户，却不知道他是的确对该产品不感兴趣，还是说想买但由于种种原因暂时没买成。（2）一般来说，没买的用户数会远远大于已经买了的用户数，这会造成training set中正负样本不均衡，使train出来的model有bias。这个时候，就可以使用one class classification的方法来解决，即training set中只有已经买过该产品的用户数据，在识别一个新用户是否会买该产品时，识别结果就是“会”或者“不会”。

one class classification这如何实现呢？多类classification我们都很熟悉了，方法也很多，比如像SVM去寻找一个最优超平面把正负样本分开，总之都涉及到不止一个类的样本，相当于告诉算法这种东西长什么样（这里的长什么样指的是特征提取方法所提取到的提取），那种东西长什么样，于是训练出一个模型能够区分这些东西。问题是在one class classification只有一个类，这该怎么办呢？给大家介绍一个方法：SVDD（support vector domain description）

3、sklearn实现：OneClassSVM

sklearn之中有该算法，叫OneClassSVM

（1）参考案例：http://scikit-learn.org/stable/auto_examples/svm/plot_oneclass.html
（2）相关代码块
参数：

      kernel：核函数（一般用高斯核）
      nu：设定训练误差（0， 1]

方法：

      fit(x)：训练，根据训练样本和上面两个参数探测边界。（注意是无监督哦！）
      predict(x)：返回预测值，+1就是正常样本，-1为异常样本。
     decision_function(X)：返回各样本点到超平面的函数距离（signed distance）,正的为正常样本，
     负的为异常样本。

代码块

print(__doc__)

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.font_manager
from sklearn import svm

xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))
# Generate train data
X = 0.3 * np.random.randn(100, 2)
X_train = np.r_[X + 2, X - 2]
# Generate some regular novel observations
X = 0.3 * np.random.randn(20, 2)
X_test = np.r_[X + 2, X - 2]
# Generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))

# fit the model
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
n_error_train = y_pred_train[y_pred_train == -1].size
n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

# plot the line, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title("Novelty Detection")
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')

s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s)
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s)
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s)
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
           ["learned frontier", "training observations",
            "new regular observations", "new abnormal observations"],
           loc="upper left",
           prop=matplotlib.font_manager.FontProperties(size=11))
plt.xlabel(
    "error train: %d/200 ; errors novel regular: %d/40 ; "
    "errors novel abnormal: %d/40"
    % (n_error_train, n_error_test, n_error_outliers))
plt.show()

结果输出：

.

二、SVDD

0、SVM引入
在写SVDD之前，需要有SVM的相关基础，因为SVDD和SVM在公式推导上是很相像的。
SVM的核心是找一个有着最大间距的超平面实现二分类

1、原理引入
SVDD（（Support Vector Data Description）即支持向量数据描述，其基本思想是通过在映射到高维的特征空间中找出一个包围目标样本点的超球体，并通过最小化该超球体所包围的体积让目标样本点尽可能地被包围在超球体中，而非目标样本点尽可能地排除在超球体中，从而达到两类之间划分的目的。该方法目标是求出能够包含正常数据样本的最小超球体的中心a和半径R。

2、通俗理解
它的基本思想是，既然只有一个class，那么我就训练出一个最小的超球面（超球面是指3维以上的空间中的球面，对应的2维空间中就是曲线，3维空间中就是球面，3维以上的称为超球面），把这堆数据全都包起来，识别一个新的数据点时，如果这个数据点落在超球面内，就是这个类，否则不是。例如对于2维（维数依据特征提取而定，提取的特征多，维数就高，为方便展示，举2维的例子，实际用时不可能维数这么低）数据，大概像下面这个样子：

有人可能会说：图上的曲线并没有把点全都包住嘛~为什么会这样呢？看原理就懂了，下面给大家讲SVDD的原理，SVDD是叫support vector domain description，想必你第一反应就是想到support vector machine(SVM)，的确，它的原理和SVM很像，可以用来做one class svm，如果之前你看过SVM原理，那么下面的讲解你将会感到很熟悉。凡是讲模型，都会有一个优化目标，SVDD的优化目标就是，求一个中心为a，半径为R的最小球面：

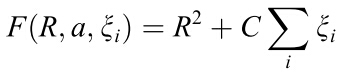
使得这个球面满足：

满足这个条件就是说要把training set中的数据点都包在球面里。
这里的 是什么东西？如果你看过SVM的话，想必你已经能猜出来它的含义了，它是松弛变量，和经典SVM中的松弛变量的作用相同 ，它的作用就是，使得模型不会被个别极端的数据点给“破坏”了，想象一下，如果大多数的数据都在一个小区域内，只有少数几个异常数据在离它们很远的地方，如果要找一个超球面把它们包住，这个超球面会很大，因为要包住那几个很远的点，这样就使模型对离群点很敏感，说得通俗一点就是，那几个异常的点，虽然没法判定它是否真的是噪声数据，它是因为大数点都在一起，就少数几个不在这里，宁愿把那几个少数的数据点看成是异常的，以免模型为了迎合那几个少数的数据点会做出过大的牺牲，这就是所谓的过拟合（overfitting）。所以容忍一些不满足硬性约束的数据点，给它们一些弹性，同时又要保证training set中的每个数据点都要满足约束，这样在后面才能用Lagrange乘子法来求解，因为Lagrange乘子法中是要包含约束条件的，如果你的数据都不满足约束条件，那就没法用了。注意松弛变量是带有下标i的，也就是说它是和每个数据点有关的，每个数据点都有对应的松弛变量，可以理解为：对于每个数据点来说，那个超球面可以是不一样的，根据松弛变量来控制，如果松弛变量的值一样，那超球面就一样。那个C嘛，就是调节松弛变量的影响大小，说得通俗一点就是，给那些需要松弛的数据点多少松弛的空间，如果C很大的话，那么在cost function中，由松弛变量带来的cost就大，那么training的时候会把松弛变量调小，这样的结果就是不怎么容忍那些离群点，硬是要把它们包起来，反之如果C比较小，那会给离群点较大的弹性，使得它们可以不被包含进来。现在你明白上面那个图为什么并没有把点全都包住了么？下图展示两张图，第一样图是C较小时的情形，第二张图是C较大时的情形：

现在有了要求解的目标，又有了约束，接下来的求解方法和SVM几乎一样，用的是Lagrangian乘子法:

注意此时，其中是由，和共同推出来的。上面的向量内积也可以像SVM那样用核函数解决：

之后的求解步骤就和SVM中的一样了，挺复杂的，具体请参考SVM原理。
训练结束后，判断一个新的数据点z是否是这个类，那么就看这个数据点是否在训练出来的超球面里面，如果在里面 ，即，则判定为属于这个类。将超球面的中心用支持向量来表示，那么判定新数据是否属于这个类的判定条件就是：

三、OCSVM与SVDD的比较