数值计算方法(Numerical Methods)MATLAB实现(1)---Gauss消元法、Doolittle分解

（1）—高斯消元法
       1.1 消去阶段
   假设系数矩阵前k行已被转化为上三角矩阵形式。当前枢轴方程(作为被减量的方程) 是第K行的方程，其下所有方程都待转换为下三角形式。

    假设现要消去第i行的方程，也即系数A_ik要被消去。将这行减去A_kk×λ(A_ik/A_kk)，即可实现。对应的改变为：
A_ij ← A_ij − λA_kj , j = k, k + 1, … , n
b_i ← b_i − λb_k

     为将全部系数矩阵转化为上三角形，k的范围应为1，2，…，n-1（用来选择被减行）；i的范围应为k+1，k+2，…，n(用来选择要转化的行)。对应MATLAB程序如下：

for k = 1:n-1
    for i = k+1 :n
        if A(i,k) ~= 0
            lambda = A(i,k)/A(k,k);
            A(i,k+1:n) = A(i,k+1:n) - lameda * A(k,k+1:n);
            b(i) = b(i) - lambda *b(k);
        end
    end
end

为了避免冗余操作，以上算法作出了如下改进：
     如果A_ik恰好为0，就忽略第i行转换
     下标j始于k+1而不是k。所以，A_ik并不为0，而是维持原始值。因为后续求解过程没有用到系数矩阵下三角部分，所以这些位置的元素与求解无关。

      1.2 回代阶段
      高斯消去后的增广矩阵格式如下。

     考虑回代过程中x_n,x_n-1,x_n-2,…,x_k+1已被解出的阶段，要从第K个方程中找出x_k的解。
A_kk x_k + A_k,k+1x_k+1 +···+ A_knx_n = b_k

这个问题的解是

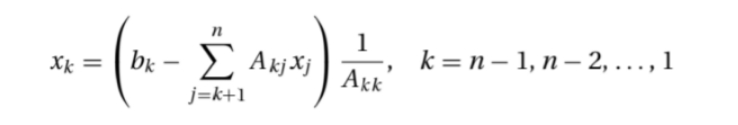
对应的MATLAB程序是：

for k = n:-1:-1
    b(k) = (b(k)-A(k,k+1:n)*b(k+1:n))/A(k,k)
end

      算法复杂度分析：
      强烈依赖于乘除操作。消元阶段大约有n³/2次操作，回代阶段约有n²/2次。可见，大多数算力用在了消元阶段。

      完整程序

function [x,det] = gauss(A,b)

    if size(b,2) > 1; b = b';
    end % b must be column vector
    n = length(b)
    for k = 1:n-1
        for i = k+1 :n
            if A(i,k) ~= 0
                lambda = A(i,k)/A(k,k);
                A(i,k+1:n) = A(i,k+1:n) - lameda * A(k,k+1:n);
                b(i) = b(i) - lambda *b(k);
            end
        end
    end
    if nargout == 2;det = prod(diag(A));   
    end
    for k = n:-1:-1
        b(k) = (b(k)-A(k,k+1:n)*b(k+1:n))/A(k,k);
    end
    x = b;
end

      举例
      使用高斯消元法解系数矩阵为MATLAB由v = [0 1 0 1 0 1]^T生成的范德蒙矩阵,常量矩阵为[0 1 0 1 0 1]^T方程。

%在上述程序基础上
A = vander(1:0.2:2);
b = [0 1 0 1 0 1]';

format long
[x,det] = gauss(A,b)

     解得

x =

1.0e+04 *

0.041666666667010
-0.312500000002465
0.925000000006972
-1.350000000009722
0.970933333340017
-0.275100000001813
反代A*x验证正确性
ans =

-0.000000000000909
0.999999999997726
-0.000000000005912
0.999999999984084
-0.000000000054115
0.999999999949978
在允许的舍入误差范围内，x的解是精确的。
（2）- LU分解
      2.1 杜丽特分解
     考虑一3*3矩阵，假设存在三角矩阵L,U，使得A = LU。

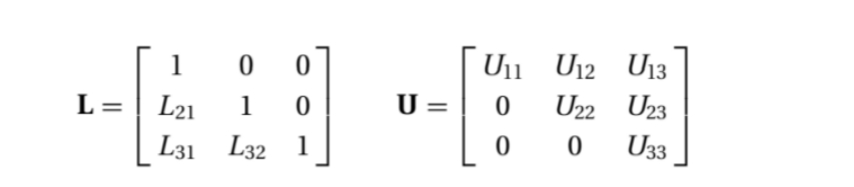
        将LU相乘，得到

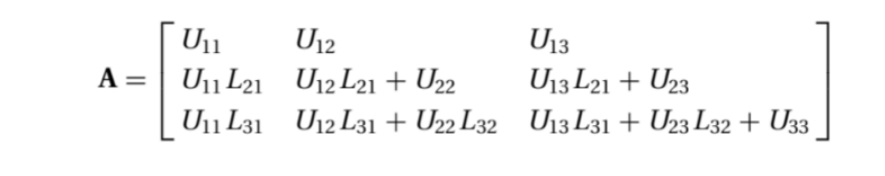
       对上式进行高斯消元。先选取第一行为被减行，第二行减去L₂₁×第一行，第三行减去L₃₁×第一行，得到

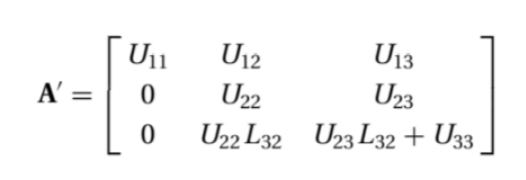
     以此类推，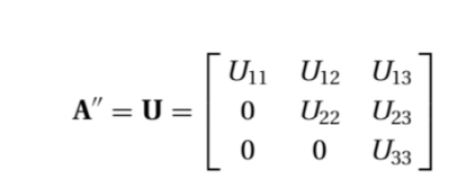
     容易看出，通常在系数矩阵下三角部分存储乘数，代替被消去的系数。L的对角线元素程序默认是1，不用被存储。所以L、U通常合并表示成

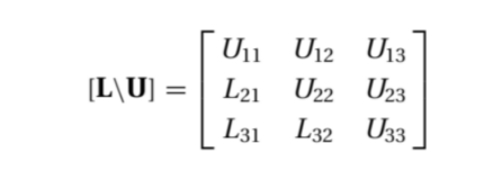
      书写程序时，在高斯消元法的基础上，只需将乘数λ存储到对应下三角矩阵位置。
      LU分解算法上与高斯消元法一致，即长操作次数约为n³/3。
      如下给出LU分解过程代码：

function A = lu_decomposition(A)
    n = size(A,1);
    for k = 1:n-1
        for i = k+1 :n
            if A(i,k) ~= 0.0
                lambda = A(i,k)/A(k,k);
                A(i,k+1:n) = A(i,k+1:n) - lambda * A(k,k+1:n);
                A(i,k) = lambda;
            end
        end
    end
end

      求解阶段，从前向后依次代入即可求出Ly = b中的y。得到y，便可由Ux = y求出x。为求y_k，解第k个方程，得出

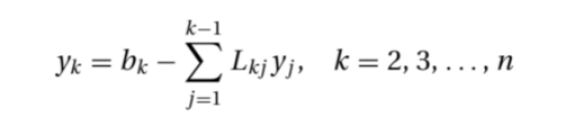
for k = 2:n
b(k)= b(k) - A(k,1:k-1)*y(1:k-1);
end

      Ux = y求出x的过程与高斯消元法相同。如下是求解阶段代码。

function x = LUsol(A,b)%used to solve L*U*x = b, A contains L and U
    if size(b,2) > 1; b = b'; end
    n = length(b);
    for k = 2:n
        b(k) = b(k) - A(k,1:k-1)*b(1:k-1);
    end
    for k = n:-1:1
        b(k) = (b(k) - A(k,k+1:n)*b(k+1:n))/A(k,k);
    end
    x = b;
end

      例子：使用杜丽特分解法解方程Ax = b，并计算|A|

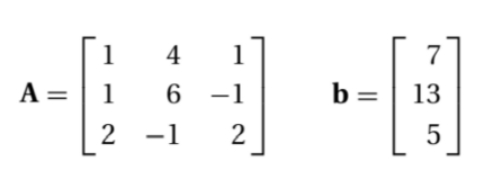
function A = lu_decomposition(A)
    n = size(A,1);
    for k = 1:n-1
        for i = k+1 :n
            if A(i,k) ~= 0.0
                lambda = A(i,k)/A(k,k);
                A(i,k+1:n) = A(i,k+1:n) - lambda * A(k,k+1:n);
                A(i,k) = lambda;
            end
        end
    end
end

function x = LUsol(A,b)

    if size(b,2) > 1; b = b'; end
    n = length(b);
    for k = 2:n
        b(k) = b(k) - A(k,1:k-1)*b(1:k-1);
    end
    for k = n:-1:1
        b(k) = (b(k) - A(k,k+1:n)*b(k+1:n))/A(k,k);
    end
    x = b;
end

在命令行中输入：

A = [3 -1 4; -2 0 5; 7 2 -2];
B = [6 -4; 3 2; 7 -5];
A = lu_decomposition(A);
det = prod(diag(A))
for i = 1:size(B,2)
X(:,i) = LUsol(A,B(:,i));
end

得到