数据结构之红黑树插入案例详解

目录

一、概述

二、红黑树插入案例

三、总结

---

一、概述

前面一篇文章介绍了红黑树插入的几种情况以及怎么自平衡操作，但是理论知识比较多，不好理解，今天我们用一个简单的示例总结一下前面的一些自平衡操作，包括变色、左旋、右旋等。

二、红黑树插入案例

【a】首先我们先准备一颗已经平衡的红黑树，如下图：

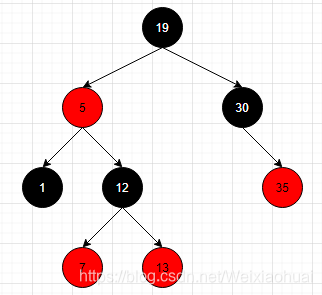
可见，已经满足红黑树五大特性：

• 性质1：节点是红色或黑色；
• 性质2：根节点是黑色；
• 性质3：每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)；
• 性质4：从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点；
• 性质5：每个叶子的节点都是黑色的空节点（NULL）；

【b】下面我们插入节点6

大家都知道，插入包括查找插入位置和插入操作两个步骤，首先我们根据红黑树左子树节点值比跟节点小，右子树节点值比跟节点大的特性，挨个比较，找到插入位置，大体流程：

1. 比较6和19，因为6<19，所以到19的左子树继续查找；
2. 比较6和5，因为6>5，所以到5的右子树继续查找；
3. 比较6和12，因为6<12，所以到12的左子树进行查找；
4. 比较6和7，因为6<7，所以到7的左子树进行查找；
5. 因为节点7已经是叶子节点，所以直接在7的左子树位置直接插入；

插入后的红黑树如下图：

观察上面的红黑树，因为新插入的元素都是红色节点，所以节点6和7两个红色节点连在一起了，不满足平衡特性，所以需要进行变色。

【c】变色

满足变色的条件：当前节点的父亲节点是红色，并且当前节点的叔叔节点也是红色，那么这个时候就需要进行变色了。

怎么变色：

1. 把父节点变为黑色；
2. 把叔叔节点也变为黑色；
3. 把祖父节点（爷爷节点）设置为红色；
4. 设置当前节点为爷爷节点；

根据上面说的变色规则，我们对上面的红黑树进行变色：

 注意：上图底下的备注信息：叔叔节点【13】应该是变为黑色，当时笔误打错字。 

变颜色之后还是存在问题：5和12两个红色节点又相连，但是此时已经不满足变颜色的条件，所以不能通过变颜色来解决，只能依靠旋转来处理了。

【d】左旋

满足左旋的条件：当前节点的父亲节点为红色，叔叔节点是黑色的时候，并且当前节点是父亲节点的右子树，则满足左旋条件。

• 怎么左旋：以当前节点的父亲节点为旋转点进行左旋。

根据上面左旋的条件，我们对上面红黑树中当前节点12的父亲节点5为旋转点进行左旋，左旋后的红黑树如下图：

 

 

存在问题：5和12两个红色节点还是连接在一起

【e】右旋

虽然当前节点5的父亲节点12是红色，叔叔节点是黑色，但是5在父亲节点12的左子树，所以不满足左旋条件，那么我们就需要考虑右旋。

满足右旋的条件：当前节点的父亲节点是红色，叔叔节点是黑色，并且当前节点在父亲节点的左子树，则需要进行右旋。

怎么右旋：

1. 把父亲节点变为黑色【12变黑色】
2. 把爷爷节点变为红色【19变红色】
3. 以当前节点的爷爷节点（祖父节点）为旋转点进行右旋操作【以19节点右旋】

可见， 右旋比左旋多了一个变颜色的步骤，根据上面描述的右旋条件，我们对上面的红黑树进行右旋，右旋后的红黑树如下图：

 

至此，经过变色、左旋、右旋后的红黑树已经平衡，以上就是红黑树插入元素后并且自平衡的详细过程。

三、总结

上述仅仅只是一个稍微简单的红黑树插入示例，整个过程图总结如下：