均方误差损失（MSE loss）—最常用的回归（Regression）损失

均方误差损失（MSE loss）—最常用的回归（Regression）损失

什么是均方误差损失？

假设我们有真实值：

$$y\_\text{true}=y=\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]$$

和预测值：

$$y\_\text{pred}=\hat{y}=\left[\begin{array}{c}\widehat{y_1}\\ \widehat{y_2}\\ \widehat{y_3}\end{array}\right]$$

均方误差（Mean Square Error）损失可以写为：

$$\begin{array}{rl}MSE& =\frac{1}{N}\sum _{i=1}^{i=N}(y\_{\text{true}}_i-y\_{\text{pred}}_i{)}^2\\ MSE& =\frac{1}{N}\sum _{i=1}^{i=N}(y_i-\widehat{y_i}{)}^2\\ ⟹MSE& =\frac{1}{3}[(y_1-\widehat{y_1}{)}^2+(y_2-\widehat{y_2}{)}^2+(y_3-\widehat{y_3}{)}^2]\end{array}$$

在Python中，利用Numpy，均方误差损失可以写为：

import numpy as np
np.random.seed(2001716)

# defining MSE
def mse(y_true, y_pred):
    return np.mean((y_true - y_pred) ** 2)

如何计算MSE的梯度？

真实值$y\_\text{true}$固定，MSE的值与$y\_\text{pred}$有关，也即与$(\widehat{y_1},\widehat{y_2},\widehat{y_3})$有关。

$$MSE=f(\widehat{y_1},\widehat{y_2},\widehat{y_3})$$

MSE的Jacobian矩阵（函数的一阶偏导数以一定方式排列而成的矩阵）为：

$$J=\frac{\partial (MSE)}{(\widehat{y_1},\widehat{y_2},\widehat{y_3})}=\left[\begin{array}{c}\frac{\partial (MSE)}{\partial (\widehat{y_1})}\\ \\ \frac{\partial (MSE)}{\partial (\widehat{y_2})}\\ \\ \frac{\partial (MSE)}{\partial (\widehat{y_3})}\end{array}\right]$$

分别计算Jacobian矩阵中的每一个元素得到：

$$\begin{array}{rl}& ⟹J=\left[\begin{array}{c}\frac{-2(y_1-\widehat{y_1})}{3}\\ \\ \frac{-2(y_2-\widehat{y_2})}{3}\\ \\ \frac{-2(y_3-\widehat{y_3})}{3}\end{array}\right]\\ & ⟹J=-\frac{2}{3}(\left[\begin{array}{c}{y}_1-\widehat{y_1}\\ \\ y_2-\widehat{y_2}\\ \\ y_3-\widehat{y_3}\end{array}\right])\\ & ⟹J=-\frac{2}{3}(\left[\begin{array}{c}{y}_1\\ \\ y_2\\ \\ y_3\end{array}\right]-\left[\begin{array}{c}\widehat{y_1}\\ \\ \widehat{y_2}\\ \\ \widehat{y_3}\end{array}\right])\\ & ⟹J=-\frac{2}{3}(y\_\text{true}-y\_\text{pred})\end{array}$$

其中，‘3’代表$y\_\text{true}$和$y\_\text{pred}$中标量元素的个数。

在Python中，利用Numpy，均方误差损失的Jacobian矩阵可以写为：

# defining MSE gradients

def mse_grad(y_true, y_pred):
    N = y_true.shape[0]
    return -2 * (y_true - y_pred) / N

MSE的优缺点

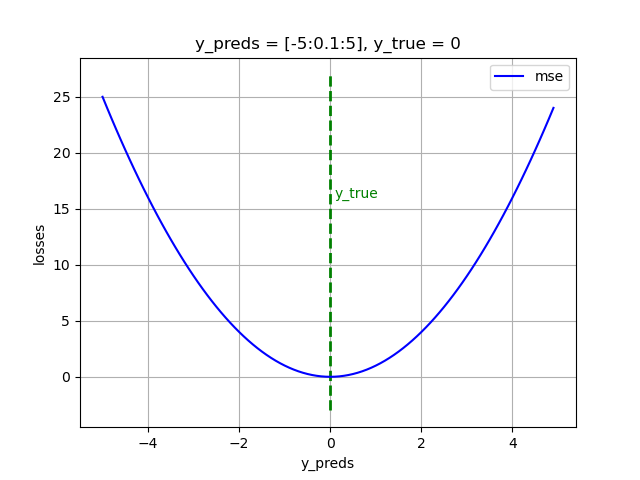
😀优点：MSE由于存在(y_true - y_pred)平方项，能够保证被训练的模型不会产生具有较大误差的预测；同时使用MSE训练的模型收敛速度快。

☹️缺点：MSE使得被训练的模型容易受到训练数据中局外点（outliers）的影响，模型的某一个无关紧要的小错误都会被MSE的平方项放大，造成对模型本身严重的影响。在现实应用中，我们不需要关心那些局外点，只需要关心模型在数据集的主要部分上的性能。

MSE loss over.