spss——主成分分析详解

概念

• 一个非监督学习的降维方法
• 只需要特征值分解，就可以对数据进行压缩，去噪
• 旨在利用降维思想，把多指标转化为少数几个的综合指标
• 每个主成分都能够反映原始变量的大部分信息，且信息不重复

应用场景

在一个图像矩阵中，有些元素特征不明显，很难用来做识别，而有些元素特征很明显，表明其方差很大（元素的方差可以度量其相对整个样本的离散度），这些元素就可以作为图像识别的主要依据，

PCA的作用就是，去除那些方差小，特征不明显的维，保留方差大，特征明显的维

优缺点

优点

仅仅需要以方差衡量信息量，不受数据集其他因素的影响

各主成分正交，

计算方法简单，主要运算是特征值分解，易于实现

缺点

主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强

方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响

spss实例

1、如果有缺失值，要先对数据进行处理

2、将处理好后的数据导入spss

3、找到主成分分析

4、将除分类列外其他导入，我的这个案例中，有一列考核列，也不需要放入，因为不属于影响因素

5、勾选系数：因为要生成成分得分系数矩阵进行最后的得分计算

6、勾选碎石图：可以更直观的主成分分布，点击确定


点击确认后经过计算。导出结果为

7、观察总方差解释图：提取提取载荷平方和的个数，就是主成分个数，最后一个主成分的占比就是选取的所有的主成分的占比总和

8、将原始特征数据进行标准化

勾选：将被抓另存变量


9，通过系数得分矩阵和标准化数据进行对应相乘

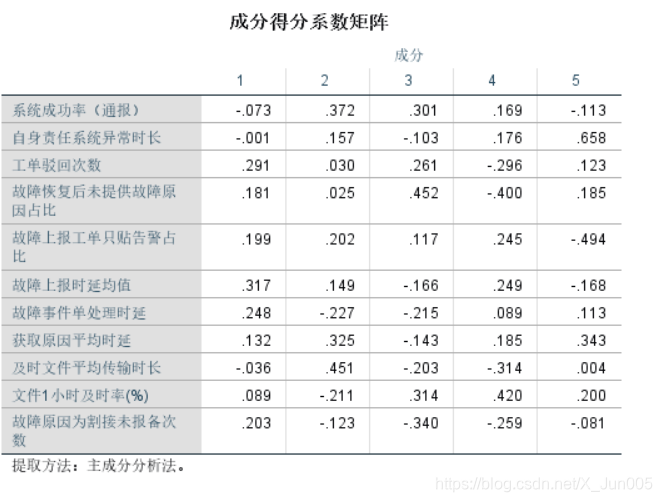
计算过程

x就是所有的特征变量

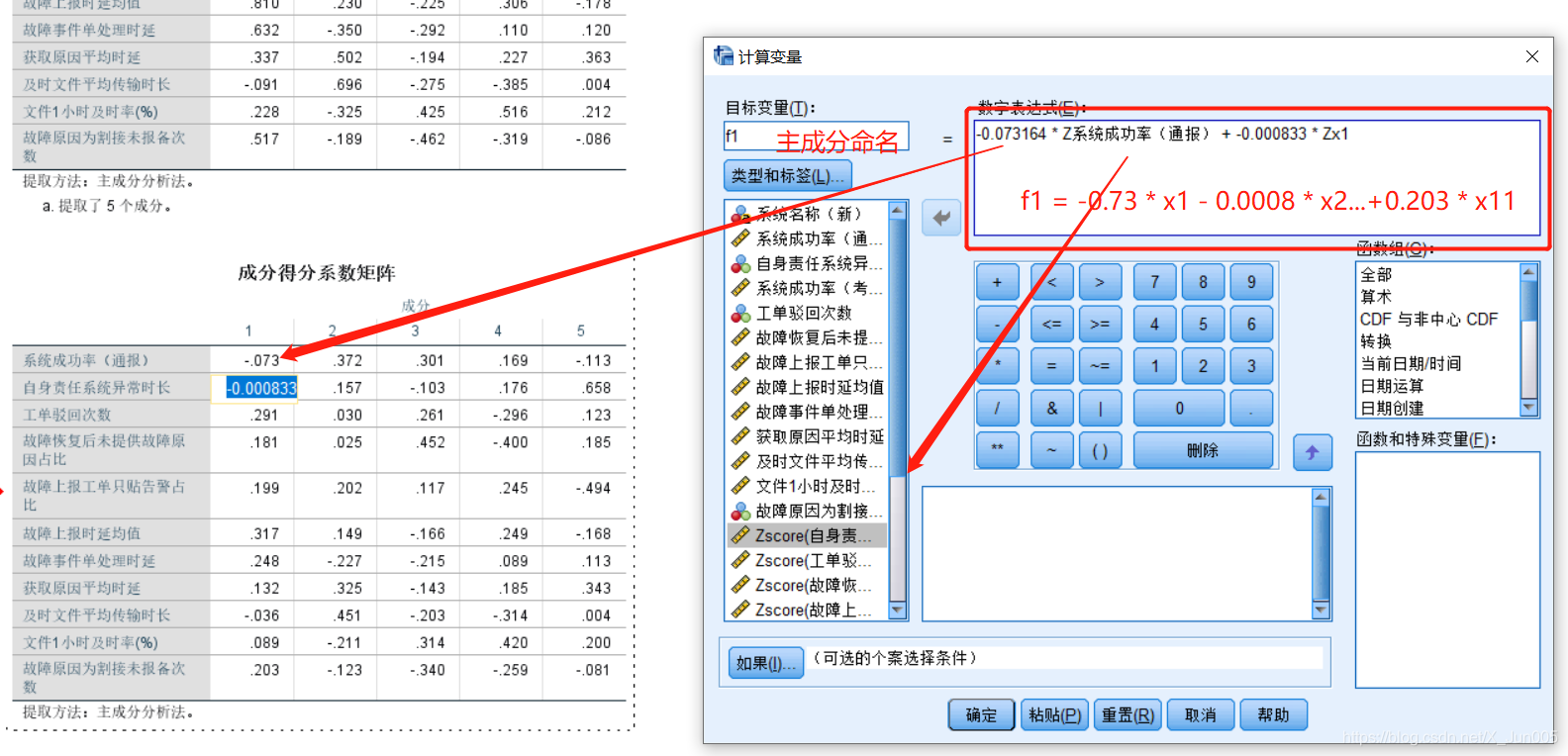
$$f1=-0.073\ast X1+-0.0008\ast X2）...+0.203\ast X11$$
$$f2=-0.372\ast X1+-0.157\ast X2）...-0.123\ast X11$$
$$F=（23.2/70.3）f1+(14.0/70.3)f2...$$