时间复杂度与空间复杂度

算法（Algorithm）是指用来操作数据、解决程序问题的一组方法。对于同一个问题，使用不同的算法，也许最终得到的结果是一样的，但在过程中消耗的资源和时间却会有很大的区别。

那么我们应该如何去衡量不同算法之间的优劣呢？

主要还是从算法所占用的「时间」和「空间」两个维度去考量。

• 时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。
• 空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述。

一、时间复杂度

对于时间复杂度的计算，业内有一种特殊的方法——大O表示法

大O表示法（Big O notation）是一种用于描述算法复杂度和性能的数学符号表示方法。在计算机科学中，算法的效率取决于输入规模的增长速度，而大O表示法就是用来描述算法在最坏情况下的时间复杂度。大O表示法中的O是“order of magnitude”的缩写，表示算法运行时间的数量级。

【O(1)】

int a = 123;
int b = 423;
int c = 231
int sum = a+b+c;

这是一个较为复杂的计算，但是无论代码执行了多少行，无论加减多少个数字，只要是没有循环等复杂结构，那这个代码的时间复杂度就都是O(1)，即常数阶。

【O(n)】

for(i=1; i<=n; ++i)
{
   k++;
}

这是一个循环语句，总共执行n次，故时间复杂度记作O(n)。在大O表示法中，时间复杂度的公式是： T(n) = O( f(n) )，其中f(n) 表示每行代码执行次数之和，而 O 表示正比例关系，这个公式的全称是：算法的渐进时间复杂度。

下图展示了上述两种复杂度，从图中可以看出，O(N)呈现为一条对角线。当数据增加一个单位时，算法也随之增加一步。 也就是说，数据越多，算法所需的步数就越多。O(N)也被称为线性时间。

【O(n²)】

for(i=1; i<=n; i++)
{
   for(j=1; j<=n; j++)
    {
       k++;
    }
}

在O(n)的基础上又套了一层循环结构，i每加一，j则进行n次循环，则内部的代码(k++)被执行了n²次，故记作O(n²)。

假设这里的i与j循环次数不相同，如下：

for(i=1; i<=m; i++)
{
   for(j=1; j<=n; j++)
    {
       k++;
    }
}

此时的i共循环m次，每执行一次循环，i循环n次，共计m*n次，则时间复杂度为O(m*n)，同样是二次阶，仍记作O(n²)。

【O()】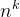

与O(n²)大同小异，O(n³)相当于三层n循环，O()相当于k层n循环，其它的类似。

【O(logn)】

int i = 1;
while(i<n)
{
    i = i * 2;
}

从上面代码可以看到，在while循环里面，每次都将 i 乘以 2，乘完之后，i 距离 n 就越来越近了。我们试着求解一下，假设循环n次之后，i 就大于 2 了，此时这个循环就退出了，也就是说 2 的 m 次方等于 n，那么 m = 
也就是说当循环 次以后，这个代码就结束了。因此这个代码的时间复杂度为：O()，称作对数阶。常见的算法二分查找的时间复杂度就是O()。

【O(nlogn)】

for(m=1; m<n; m++)
{
    i = 1;
    while(i<n)
    {
        i = i * 2;
    }
}

线性对数阶O(nlogN) 非常容易理解，将时间复杂度为O(logn)的代码循环n次的话，那么它的时间复杂度就是O(nlogN)，即线性对数阶。

【总结】

将上述几种复杂度放在一张图中观察，发现当n(即下图中的x)趋于无穷时，O(n²)>O(n)>O(1)>O(logn)，但是在n很小时却不符合这个规律，这是因为算法考虑的是最坏情况下的最优解，在需要处理的数据很大时，需要考虑复杂度的大小。

二、空间复杂度

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，我们用 S(n) 来定义。

除了时间复杂度，大O表示法还可以用来描述算法的空间复杂度，即算法所需的额外空间与输入规模之间的关系。同样地，空间复杂度也可以用O(n)等形式来表示。空间复杂度比较常用的有：O(1)、O(n)、O(n²)

【空间复杂度 O(1)】

如果算法执行所需要的临时空间不随着某个变量n的大小而变化，即此算法空间复杂度为一个常量，可表示为 O(1)

int a = 1;
int b = 2;
int sum = a + b;

代码中的 a,b,sum 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)。

【空间复杂度 O(n)】

int* a = new int(n); //在堆上动态分配了一个包含 n 个整数元素的数组
                     //new 运算符返回分配的内存块的第一个元素的指针，并将其赋值给指针变量 a
for (int i = 0; i < n; i++) 
{
    a[i] = i;        //在循环内部，这行代码将 i 的值赋给数组 a 的第 i 个元素。由于数组是从零开始索引的，第一个元素是 a[0]，第二个元素是 a[1]，依此类推。
} 

首先在堆上动态分配了一个包含 n 个整数元素的数组，这个数据占用的大小为n，new 运算符返回分配的内存块的第一个元素的指针，并将其赋值给指针变量 a。在循环内部，这行代码将 i 的值赋给数组 a 的第 i 个元素。由于数组是从零开始索引的，第一个元素是 a[0]，第二个元素是 a[1]，依此类推。虽然有一个for循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行，即随着n的增大，开辟的内存大小呈线性增长，即 O(n)。

---

在C++中，有两种主要的内存分配方式：静态内存分配和动态内存分配。静态内存分配是在编译时分配内存，例如在函数中声明一个局部变量，或者在全局范围内声明一个变量。而动态内存分配是在程序运行时根据需要分配内存。

new 运算符用于动态分配单个对象或对象数组的内存。它在堆上分配内存，并返回指向分配的内存块的指针。语法上，new 后跟要分配的数据类型，可以是单个对象类型或数组类型，例如 new int 或 new int[10]。

需要注意的是，使用 new 分配的内存必须在不再需要时使用 delete 或 delete[ ] 运算符进行显式释放，以避免内存泄漏。delete 用于释放通过 new 分配的单个对象的内存，而 delete[ ] 用于释放通过 new 分配的对象数组的内存。

需要注意的是，从C++11开始，推荐使用智能指针（如 std::unique_ptr 或 std::shared_ptr）来管理动态分配的内存，以避免手动释放内存的复杂性和潜在的内存泄漏问题。