GDOI2016 之 GDSOI 第一题 互补约数

互补约数

题目大意

已知函数

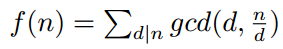
求它的前缀和函数

输入格式

输入包含一行，一个正整数 n。

输出格式

输出只有一行， F(n)。

样例输入

Sample Input 1
10

Sample Input 2
1000

输出格式

Sample Output 1
32

Sample Output 2
12776

数据范围

20分算法

虽然侥幸进了决赛，但还是只能想到20分的。
不难看出，题目让我们求的是

$\sum_{i=1}^{n}$$\sum_{j=1}^{\lfloor{n \over i}\rfloor}$$gcd(i,j)$。

这样子枚举一下$i$，$j$，再打个gcd，求一下和就可以了。
这样20分就弄到手了。

100分算法

100分算法要用到莫比乌斯反演。
想学的可以自已查一下。
这里简单介绍它的内容。
mu(i)表示莫比乌斯函数。
如果满足

$F_n=\sum_{d|n}G_d$

则满足

$G_n=\sum_{d|n}F_d*mu({n \over d})$

还有变式。
如果满足

$F_i=\sum_{d=1}^{\lfloor{n \over i}\rfloor}G_{i*d}$

则有

$G_i=\sum_{d=1}^{\lfloor{n \over i}\rfloor}F_{i*d}*mu(d)$

如果想学的可以看我写的博客，链接如下:
http://blog.csdn.net/xianhaoming/article/details/51519100

好，介绍完了，现在进入正题。
我们设$f_k$表示$gcd(i,j)=k$的对数，$g_k$表示$k|gcd(i,j)$的对数。其中一定满足题目$gcd(i,j)≤\sqrt{n}$。
则现在满足

$g_k$=$\sum_{i=1}^{\lfloor{\sqrt{n} \over k}\rfloor}$$f_{k*i}$

根据莫比乌斯反演，得

$f_k$=$\sum_{i=1}^{\lfloor{\sqrt{n} \over k}\rfloor}$$g_{k*i}*mu(i)$

那这样我们要求的答案就变成了

Ans=$\sum_{k=1}^{\sqrt{n}}$$k$*$f_k$

=$\sum_{k=1}^{\sqrt{n}}$ $k$*$\sum_{l=1}^{\lfloor{\sqrt{n} \over k}\rfloor}$$g_{k*l}*mu(l)$

我们设

$s$=$l$*$k$

则

Ans=$\sum_{s=1}^{\sqrt{n}}$ $g_s$*($\sum_{d|s}$ $mu(d)*{s\over d}$)

我们发现$\sum_{d|s}$ $mu(d)*{s\over d}$这一段只跟$s$有关，所以我们把此式子换成$W_s$，则

Ans=$\sum_{s=1}^{\sqrt{n}}$ $g_s$*$W_s$

我们先说一下$W$数组怎么预处理。
我们发现很多$mu(i)$的值为0，对$W$没有贡献。
于是我们可以这么处理：

    E:=trunc(sqrt(N));
    for i:=1 to E do
    if mu[i]<>0 then
    for l:=1 to E div i do
    M[i*l]:=M[i*l]+mu[i]*l;

现在我们看一下$g_s$怎么求。
易得

$g_s$=$\sum_{i=1}^{{n} \over {s^2}}$$\lfloor{n\over {i*s^2}}\rfloor$

现在我们尝试优化这个式子的时间复杂度。
我们发现对于多对（i，j），存在

$\lfloor{n\over {i*s^2}}\rfloor$=$\lfloor{n\over {j*s^2}}\rfloor$

这是我们可以分块，把一段$\lfloor{n\over {i*s^2}}\rfloor$的值相等的一段一次求完，这样就可以大大降低时间复杂度。详细做法见程序。

Code (pascal)

var
    bz:array[0..400000] of boolean;
    mu,jh,ss:array[0..400000] of int64;
    j,k,l,i:longint;
    cqy:extended;
    n,m,lj,P,O,bj,le,r,ans,pp:int64;
function min(a,b:INT64):INT64;
    begin
        if a<b then exit(a)
        else exit(b);
    end;
begin
    assign(input,'gcd.in'); reset(input);
    assign(output,'gcd.out'); rewrite(output);
    readln(n);
    m:=trunc(sqrt(n));
    mu[1]:=1;
    for i:=2 to m+1 do
    begin
        if bz[i]=false then
        begin
            inc(o);
            ss[o]:=i;
            mu[i]:=-1;
        end;
        for l:=1 to o do
        begin
            if ss[l]*i>m then break;
            bz[ss[l]*i]:=true;
            mu[ss[l]*i]:=-mu[i];
            if i mod ss[l]=0 then
            begin
                mu[ss[l]*i]:=0;
                break;
            end;
        end;
    end;
    for i:=1 to m+1 do
    if mu[i]<>0 then
    for l:=1 to m div i do
    jh[i*l]:=jh[i*l]+mu[i]*l;
    for i:=1 to m do
    begin
        le:=1;
        lj:=0;
        cqy:=n/i/i;
        bj:=n div i+1;
        while le<=bj do
        begin
            pp:=trunc(cqy/le);
            if pp<=0 then break;
            r:=min(bj,trunc(cqy/pp));
            lj:=lj+(r-le+1)*pp;
            le:=r+1;
        end;
        ans:=ans+lj*jh[i];
    end;
    writeln(ans);
    close(input);
    close(output);
end.