最大化
题目大意
给你一个n*m的网格,每个格子有一个数a_{i,j},现在要求一个面积最大的矩形,使得这个矩形内的平均值大于0,求最大面积。
数据范围
题解
先转化题目,平均值大于
0
也就意味着总和大于
首先枚举这个矩形的上下边界,对于每种情况分开做。
定义
Si
表示右边界为第
i
列,左边界为第
在上下边界已经确定的情况下,对于以第
j
列为右边界,我们需要找一个最小的
那我们怎么找
k
的值呢?
考虑二分这个值,假设当前枚举的二分值为
常数卡的好就可以过了。
Code(Pascal)
var
n,m,j,k,l,i:longint;
o,ans,le,ri,mid,u:int64;
wz:array[-1..500] of int64;
a,qz:array[0..300,0..300] of int64;
function min(a,b:int64):int64;
begin
if a<b then exit(a)
else exit(b);
end;
function max(a,b:int64):int64;
begin
if a>b then exit(a)
else exit(b);
end;
begin
readln(n,m);
for i:=1 to n do
begin
o:=0;
for l:=1 to m do
begin
read(a[i,l]);
o:=o+a[i,l];
qz[i,l]:=qz[i-1,l]+o;
end;
readln;
end;
for i:=1 to n do
for l:=i to n do
if (l-i+1)*m>ans then
begin
wz[0]:=0;
wz[1]:=min(qz[l,1]-qz[i-1,1],0);
if qz[l,1]-qz[i-1,1]>0 then u:=1
else u:=0;
for j:=2 to m do
begin
wz[j]:=qz[l,j]-qz[i-1,j];
le:=-1;
ri:=j-u-1;
while le+1<ri do
begin
mid:=(le+ri) div 2;
if wz[mid]<wz[j] then ri:=mid
else le:=mid;
end;
if wz[j]>wz[ri] then
u:=max(u,j-ri);
wz[j]:=min(wz[j],wz[j-1]);
end;
ans:=max(ans,u*(l-i+1));
end;
writeln(ans);
end.








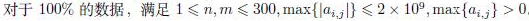














 114
114

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








