Python 算法之 求素数、质数

Python 如何求素数、质数

---

素数、质数(重点)

先明白什么是素数😣

质数，英文名：Prime number，又称为素数，指的是值大于1的 自然数中，除了1和该数自身外，无法被其他自然数整除的数，大于1的自然数若不是素数，则称之为合数，注意1既不是质数也不是合数。

题目
统计所有小于非负整数 n 的质数的数量。

示例	输入	输出	描述
一	n=10	4	小于 10 的质数有 [ 2, 3, 5, 7 ]，一共 4 个
二	n=20	8	小于 20 的质数有 [2, 3, 5, 7, 11, 13, 17, 19]，一共 8 个
三	n=1	0	素数指的是值大于1的自然数中
四	n=0	0	指的是值大于1的 自然数中

---

方法一：枚举

这种方法简单粗暴，我喜欢称之为暴力法

直接循环

def countprimes(n: int) -> int:
    res = 0
    for i in range(2, n):
        for k in range(2, int(i ** 0.5)+1):  # 求根，向下取整再+1
            if i % k == 0:                   # 能整除余数必定为 0
                break
        else:                                # 循环正常结束，没有遇到中止即为素数
            res += 1
    return res

封装函数

def countprimes(n: int) -> int:
    def is_primes(x: int) -> bool:
        for i in range(2, int(x ** 0.5)+1):  # 求根，向下取整再+1
            if x % i == 0:					 # 能整除余数必定为 0
                return False
        return True

    res = 0
    for k in range(2, n):
        if is_primes(k):
            res += 1
    return res

执行效率

• 时间复杂度：
  检查单个数是否为素数时间复杂度为O(√n)，一共有O(n)个数需要检查
  
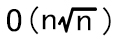
• 十分不推荐这种算法，给定的 n 数值较小时或许还可以，可一但数值大起来，那执行花费时间会很久，在 算法题 中容易造成超时🙄

---

方法二：厄拉多塞筛法【埃氏筛】

def countprimes(n: int) -> int:
    isprimes = [True] * n              # n 长度的布尔数组
    res = 0
    for i in range(2, n):
        if isprimes[i]:             
            res += 1                   # 数组值为True时 +1
            j = i
            while j * i < n:           # 被选中数的倍数不大于 n
                isprimes[j*i] = False  # 将素数的倍数都给排除
                j += 1
    return res

基于此方法，再进行优化

• 省去计数(res)操作，把布尔数值改成只有 1 和 0 的数组，根据索引 将不是素数改为0，最后统计此数组和，但要注意把 代表数值0和数值1 的索引值提前改成0，且在 n < 2时 直接返回0，否则提前改数组值时会报错

• 厄拉多塞筛法的最主要目标是，把素数的倍数都给排除掉，那么仔细想想，在循环超过一半的时候，剩下一半数的倍数还在 n 的范围内吗？举个例子，当n = 10, 循环到 6 的时候 6 x 2 > 10 ，这是没有意义的

• 精髓：在排除素数的倍数时，用到了 while 循环进行操作，那么能不能采用 列表 切片+步长 的方式 进行代替呢？

  def countprimes(n):
      if n < 2:
          return 0
      isprimes = [1] * n
      isprimes[0], isprimes[1] = 0, 0     # 只有在 n > 2时，索引0和1才存在
      for i in range(2, int(n ** 0.5)+1):
          if isprimes[i]:
              isprimes[i*i:n:i] = [0] * len(isprimes[i*i:n:i])    # 利用切片+步长方式 排除
      return sum(isprimes)
  

---

方法三：线性筛

使用厄拉多塞筛法时，其实会存在冗余的标记操作，同一个被排除的合数会被标记多次，比如18可以 2 * 9 = 18 又可以 3 * 6 = 18，造成两次标记，使用 线性筛 的目的就是让每个合数只被标记一次

差别：

• 厄拉多塞筛法是对质数的倍数进行排除
• 线性筛是对 所有整数 与 已获得的质数 相乘的值 进行排除，以发现此整数能够被 已获得的质数 整除时中止，即遇到自身的第一个质因数

def countprimes(n):
    isprime = [True] * n
    prime_arr = []					# 存储已经获得的素数
    for i in range(2, n):       
        if isprime[i]:
            prime_arr.append(i)     # 添加素数到数组中
        for k in prime_arr:         # 
            index = i * k           # 被筛选值
            if index >= n:          # 被筛选值不能大于 n
                break
            isprime[index] = False  # 将被筛选值排除
            if i % k == 0:          # 保证每个合数只会被第一个质因数筛选
                break
    return len(prime_arr)           # 统计素数数量并返回

执行效率

• 时间复杂度： O(n)

---

相关博客😏