做题计划3

[ROI 2017] 学习轨迹 (Day 2)

很牛的题，首先我们考虑暴力，枚举 $A$ 或者 $B$ 序列的一个区间，然后看另一序列中没有出现过选的区间中最大连续段的和。

图例：

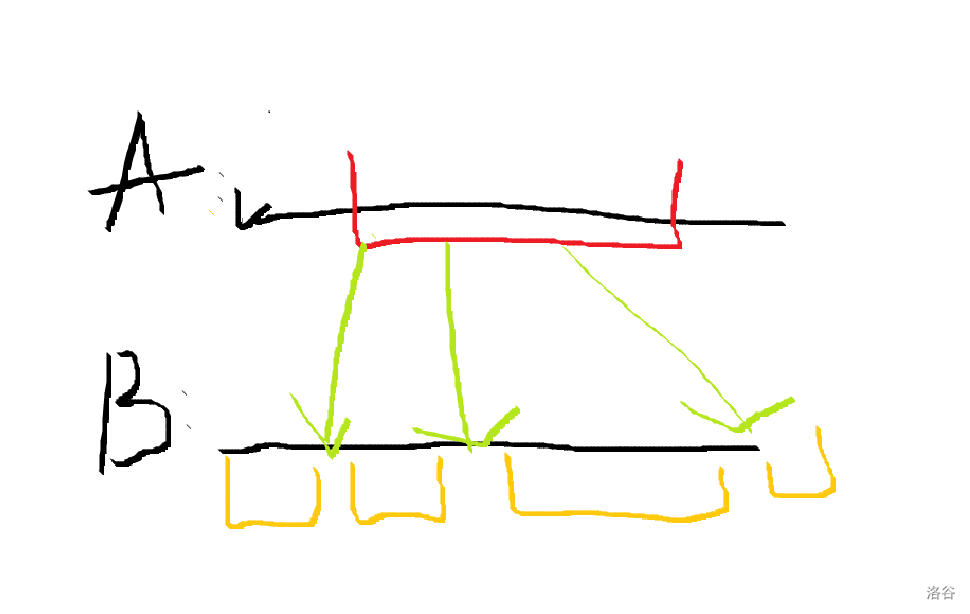
解释：假设我们选了 $A$ 中红色部分的点，然后绿线表示 $A$ 中那些数在 $B$ 中出现过，这个时候我们只能选每两个绿点之间的点(不能包括绿点)这样才能满足题意，这个东西可以通过一些预处理得到每个数 $A$ 在 $B$ 中出现的位置，然后每次一个区间，右移右端点的时候，把绿线原来所对应的区间劈开分成两半重编号可以实现，然后放到一个堆或者集合里面取最大值得到，复杂度 $O(n^2\log n)$ 理论有50。

思考一个问题，我们选的线段肯定至少有一个过某个区间的和的中点处，注意不是下标的中点，是和的中点，证明：

• 首先可以不去某个地方上课，这样可以获得某一边所有的乐趣，因为某个学校所有课程两两不同。
• 我们假设 $A$ 学校的和大于 $B$ 学校的和，假如去 $A$ 学校和去 $B$ 学校上课的区间为 $[l1,r1],[l2,r2]$ 其中满足 $[l1,r1],[l2,r2]$ 均不跨过和的中点处，那么也就是说 ${\sum }_{i=l1}^{r1}<\frac{\sum A}{2},{\sum }_{i=l2}^{r2}<\frac{\sum B}{2}$ 那加起来因为 $\sum A>\sum B$ 所以原式的和小于 $\sum A$ 不如直接全选 $A$，如果是 $\sum B>\sum A$ 同理，不予证明。

此时，再结合我们刚才说的暴力，显然我们如果枚举一个区间的话，记另一个的中点所在的绿段是 $k$ 那么一定会选另一个绿色的那一段的和加上当前区间的和，当然这里我们是假设我们此时选的区间不经过这个区间的和的中点处的。

然后我们发现了什么，扫描线啊，我们当我们固定区间右端点 $r$ 时，我们把线段树第 $i$ 个端点表示我们在这个序列选 $[i,r]$ 区间，在另一个区间选的左右端点(也就是绿色所在的段)左右端点分别是多少记为 $[L^{\prime },R^{\prime }]$，但是这样每次加入还是要遍历左端点啊，复杂度仍然是 $O(n^2\log n)$ 的。

但是我们注意到：每次加入一个点值为 $x$ 其在另一个序列中的小于值的中点位置的最大位置是 $L_x$ 大于值的中点位置的最小位置是 $R_x$ 然后实际上就是把线段树中 $[1,r]$ 中所有位置的 $L^{\prime }\leftarrow \max (L^{\prime },L_x),R^{\prime }\leftarrow \min (R^{\prime },R_x)$ 难道是吉司线段树？发现不好维护区间最大值。

但是，我们这里有个惊奇的发现就是，线段树中假设我们当前是 $[i,r]$ 那么 $[j,r],j<i$ 中 $L^{\prime }$ 的值是单调不降的，也就是越往做，线段树实际的值是越来越大的，因为限制越来越多了，也就让绿线越来越靠近那个和的中点了嘛，然后 $R^{\prime }$ 的值单调递减和上面同理，然后这样就阔以进行单调栈进行区间修改了，每个数只会进栈一次，时间复杂度很对啊。

时间复杂度 $O(n\log n)$ 的，常数有点大，因为得把 $A$ 和 $B$ 分别做一遍，看看钦定哪个作为和的中点。

代码

ARC169E

这是一个好题。

首先考虑无解，如果原串中 $R$ 的个数大于 $B$ 的个数显然无解，根据鸽巢原理可知第一层就会产生两个 $R$ 串组成一组，因为此时 $R$ 的数量至少比 $B$ 要多两个。

反正，如果 $B$ 的个数大于等于 $R$ 的个数一定有解。构造方法：

• BBBBBRRRR

这样可以把 $B$ 放到前面此时 $R$ 就没什么用了，当前也不会出现两个 $R$ 一伙，比较你 $B$ 都用不完对吧。

然后考虑一个贪心策略，我们发现如果存在一个 $B$ 他肯定是尽量匹配它后面第一个 $R$ 因为这样能够把障碍清除，并且能保留后面的 $B$。当前如果后面没有了 $R$ 那就匹配 $B$。

如果遇到了 $R$ 那么他肯定需要匹配一个 $B$ 此时匹配最后面的 $B$ 是最优的，这样能尽量保留前面的 $B$ 嘛。

我们定义一个串 $S$ 的大小表示它的字典序大小，这里我们钦定 $B$ 的字典序是小于 $R$ 的字典序的。

我们定义 $T(i)$ 表示长度为 $2^i$ 的串，满足限制下字典序最大的串，也就是尽量把 $B$ 往后放。

• 此时如果一个串 $S$ 满足 $S>T(i)$ 那这个 $S$ 肯定不合法，就相当于当前 $S$ 前面还有更多的 $R$。

我们把 $B$ 看成 1 把 $R$ 看成 -1 。记串 $S$ 的前缀和数组是 $A$ 。记 $T(i)$ 的前缀和记作 $B$ 数组。

那么 $S$ 是合法的当且仅当满足所有的 $i$ 均满足 $A_i\ge B_i$ 然后如果满足 $A_i<B_i$ 就移动过来，我们发现每移动一次，都会让前缀和大小改变 2 所以我们实际移动了前缀和的差量除以二。

代码

CF1515E

首先我们发现这很有 dp 的样子，这种 dp 不用按照特定的顺序去做，我们一般叫他连续段 dp 也叫线头 dp。

通常我们把原序列划分成若干的段，通过实现分裂，合并来计数。

比如我们设 $d{p}_{i,j}$ 表示当前序列中已经选了 $i$ 个数，组成了 $j$ 个段。

• 假如我们插入一个新的点，我们考虑以下情况：
  • 选择之前已经有的段的两段，也就是不增加新的连续段， $d{p}_{i,j}\times 2\times j\to d{p}_{i+1,j}$ 表示可以选以前已经有的连续段两端任意的一段。
  • 选择自己变成一个连续段，那么肯定在以前有的两个连续段中间或者是在第一个连续段前面或者最后一个连续段后面，那么有 $j+1$ 个空位嘛，转移自然是 $d{p}_{i,j}\times (j+1)\to d{p}_{i+1,j+1}$。
  • 要么就是合并两个连续段，就是以前两个连续段有一个间隔，然后恰好填上了，显然有 $j-1$ 个间隔，所以 $d{p}_{i,j}\times (j-1)\to d{p}_{i+1,j-1}$。

然后对于这个题来说，我们和刚刚一样，设 $d{p}_{i,j}$ 表示当前选了 $i$ 个点组成了 $j$ 个连续段，然后分为以下几种情况：

1. 插入，单独化成一个段， $d{p}_{i,j}\times (j+1)\to d{p}_{i+1,j+1}$。
2. 插入，选择之前已经有的段的两端， $d{p}_{i,j}\times 2\times j\to d{p}_{i+1,j}$。
3. 插入，选择之前已经有的段的两段，但是空出一个位置，选下一个，这样选的这个和某个端点中间就空出来一个空，根据题目定义，这个空满足左右都已经有了，所以也会出现，所以转移 $d{p}_{i,j}\times j\times 2\to d{p}_{i+2,j}$。
4. 插入，选择之前的两个段并且合并，这里分为两种不同的情况：
   • 首先就是假如两个段之间空距是 2 那么选择任意一个都能让另一个空也填上，所以每两个空之间有两种情况，转移 $d{p}_{i,j}\times 2\times (j-1)\to d{p}_{i+2,j-1}$。
   • 然后就是如果两个段之间空距是 3 那么这个时候只有选中间那个才能让这两段合并。转移 $d{p}_{i,j}\times (j-1)\to d{p}_{i+3,j-1}$。

然后这个题就通过这几种转移做完了，时间复杂度 $O(n^2)$ 空间 $O(n^2)$ 但是可以滚动数组做到 $O(n)$。

非滚动数组版本代码

滚动数组版本代码

P7967

再来道这种 dp 来练练手。

首先明确一点，假设我们最后选的磁铁其吸附范围是 $L$ 那么还剩下 $l-L$ 的长，我们把它每一个单位长度看成一个小球，并且这些小球可以放置到任意的位置，准确说是 $n+1$ 个位置，即任意两球之间或者第一个球之前，和最后一个球之后，根据插板法得到是有 $C_{l-L+n}^n$ 的情况的，于是贡献就是 $C_{l-L+n}^n\times $ 最终长度是 $k$ 的方案数了。

那么该怎么求这个方案数呢？

考虑连续段 dp，设 $f_{}$