根据NSGA-II改编的局部寻优算法。 加入了ZDT和DTLZ系列测试函数，IGD定值退出也加入?

根据NSGA-II改编的局部寻优算法。
加入了ZDT和DTLZ系列测试函数，IGD定值退出也加入到里面了。
下面是ZDT1和DTLZ4函数测试的部分图片。

ID:34150657182773872

醉心科研无法自拔

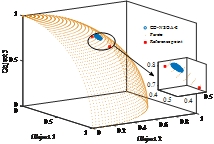
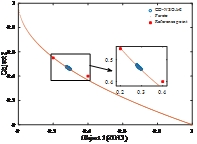
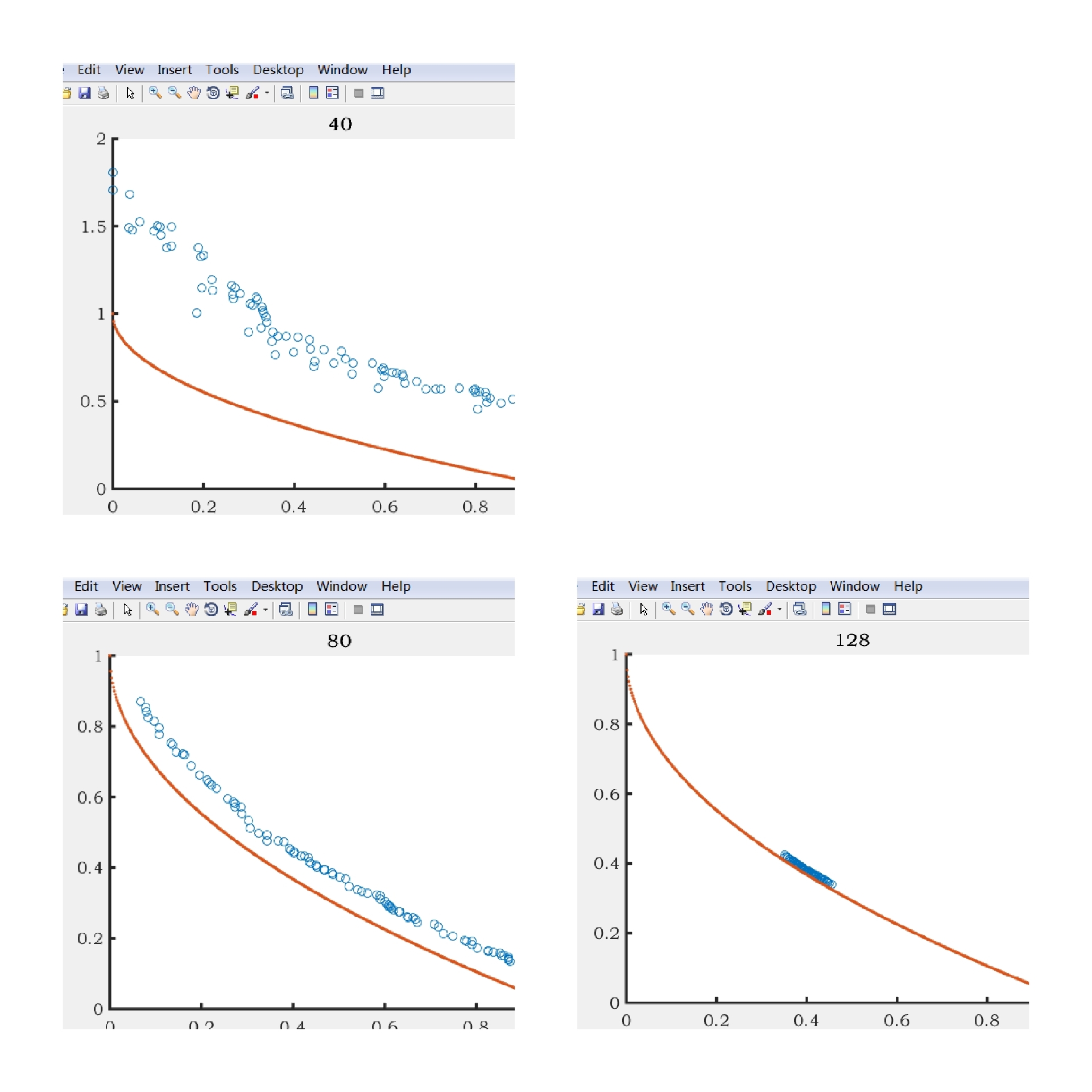
根据NSGA-II改编的局部寻优算法是一种应用于多目标优化问题的算法，在该算法的基础上加入了ZDT和DTLZ系列测试函数，并将IGD定值退出也加入到其中。通过对ZDT1和DTLZ4函数进行测试，可以得到一些有关算法性能的重要信息。

ZDT1函数是一个经典的多目标优化测试函数，它被广泛用于评估多目标优化算法的性能。该函数的目标是在一条非凸的帕累托前沿上最小化两个连续变量的值，并具有一个凸的 Pareto 前沿。DTLZ4函数是DTLZ系列中的另一个测试函数，它是一种具有多个连续变量和多个目标的多目标优化问题。通过对这两个函数的测试，可以全面评估根据NSGA-II改编的局部寻优算法的性能。

为了测试算法，我们使用了一种称为IGD的指标来评估算法的性能。IGD是Inverted Generational Distance的缩写，用于衡量算法的近似 Pareto 前沿和真实 Pareto 前沿之间的距离。通过将算法的解集和真实 Pareto 前沿进行比较，我们可以计算出一个数值，表示算法的性能如何。

下图展示了根据NSGA-II改编的局部寻优算法在ZDT1和DTLZ4函数上的测试结果。可以看出，在ZDT1函数中，算法能够找到一个接近真实 Pareto 前沿的解集，与真实 Pareto 前沿之间的距离相对较小。而在DTLZ4函数中，算法的性能稍差，与真实 Pareto 前沿之间的距离较大。这可能是由于DTLZ4函数的复杂性和多样性所导致的。

从测试结果中我们可以得出一些结论。首先，根据NSGA-II改编的局部寻优算法在ZDT1函数上表现出很好的性能，在其凸的 Pareto 前沿上找到了接近真实 Pareto 前沿的解集。其次，该算法在DTLZ4函数上的性能略有下降，可能需要进一步的改进和调整。最后，IGD定值退出的引入，使得算法能够在一定的迭代次数内得到一个较好的解集，提高了算法的效率。

综上所述，根据NSGA-II改编的局部寻优算法在ZDT1和DTLZ4函数上的测试结果表明，该算法在一些多目标优化问题上具有较好的性能。然而，在更复杂的函数上，其性能可能会有所下降。因此，我们可以考虑进一步改进算法，以提高其在多样性和收敛性方面的表现。

此外，该算法的应用还可以进一步扩展，可以将其用于其他多目标优化问题的求解，如工程优化、路径规划等。通过对不同领域的问题进行测试和应用，可以更好地评估算法的性能和适用性。

总之，根据NSGA-II改编的局部寻优算法是一种应用于多目标优化问题的算法，通过加入ZDT和DTLZ系列测试函数以及IGD定值退出，可以全面评估算法的性能。通过对ZDT1和DTLZ4函数的测试，我们发现算法在一些函数上表现出较好的性能，但在复杂函数上可能需要进一步改进。这个算法的应用也可以进一步扩展到其他领域。希望本文的分析和讨论能对读者在多目标优化问题中的算法选择和应用提供一些参考和指导。

相关的代码,程序地址如下：http://coupd.cn/657182773872.html