Information Theory in Data Mining & Decision Trees learning

最新推荐文章于 2022-02-26 15:14:23 发布

右点点

最新推荐文章于 2022-02-26 15:14:23 发布

阅读量1.1k

点赞数

Information Theory

IT provides a powerful framework for dealing withsymbolic data.(和numeric相对)

y : symbolic attribute of arity Ay
• Information content 信息含量of one of Ay values of y, yi:
I(yi) = -log2 p(yi) 负的yi概率的对数，
• It is expressed in bits
• 可以理解成“惊讶程度”。 Ay的概率越大，信息含量越小，越不值得一提

举例：

• 属性“颜色”有红绿蓝三种可能
• 一共1000条记录: 红350 绿450 蓝200

I(y=blue) = -log2(0.2)= -log(0.2)/log(2) = 2.322 bits

I(y=red) = -log2(0.35) = -log(0.35)/log(2) = 1.515 bits

I(y=green) = -log2(0.45) = -log(0.45)/log(2) = 1.152 bits

如果yi的概率是1，那么信息含量为零，因为，不要取样也知道，没什么新信息，没什么可以surprise的

信息含量不能小于零

熵：

如果有一枚理想的硬币，其出现正面和反面的机会相等，则抛硬币事件的熵等于其能够达到的最大值。我们无法知道下一个硬币抛掷的结果是什么，因此每一次抛硬币都是不可预测的。

另一个稍微复杂的例子是假设一个随机变量X，取三种可能值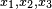 $\begin{smallmatrix} x_1, x_2, x_3 \end{smallmatrix}$ ，概率分别为 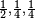$\begin{smallmatrix} \frac{1}{2}, \frac{1}{4}, \frac{1}{4} \end{smallmatrix}$ ，那么编码平均比特长度是： $\begin{smallmatrix} \frac{1}{2} \times 1 + \frac{1}{4} \times 2 + \frac{1}{4} \times 2 = \frac{3}{2} \end{smallmatrix}$ 。其熵为3/2。