【Matlab】遗传算法 程序结果

（1）针对前面的遗传算法部分，给出程序汇总如下：

%-------------函数说明----------------

%

%             主函数      

%---------------------------------------

function main()

clear

clc

popsize = 100;     %种群大小

chromlength = 10;  %二进制编码长度

pc = 0.6;          %交叉概率

pm = 0.001;        %变异概率

pop = initpop(popsize,chromlength);   %初始种群

 

  for i=1:100

     [objvalue] = cal_objvalue(pop);     %计算适应度值（函数值）

      fitvalue = objvalue;

     [newpop] = selection(pop,fitvalue);  %选择操作

     [newpop] = crossover(newpop,pc);     %交叉操作

     [newpop] = mutation(newpop,pm);      %变异操作

      pop = newpop;                %更新种群

      [bestindividual,bestfit]=best(pop,fitvalue);%寻找最优解

      x2 = binary2decimal(bestindividual);

   

      x1 = binary2decimal(newpop);

      [y1] = cal_objvalue(newpop);    

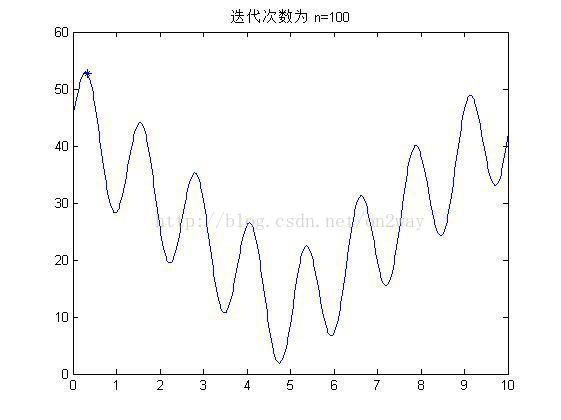
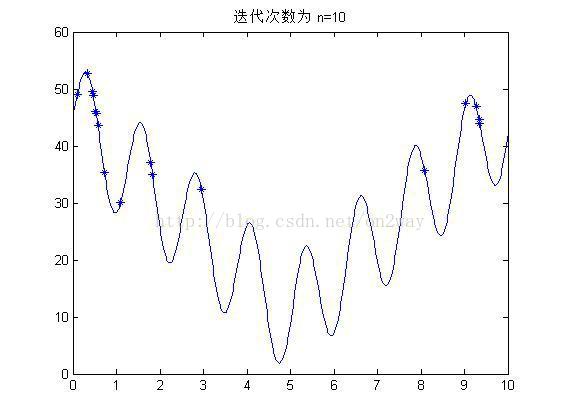
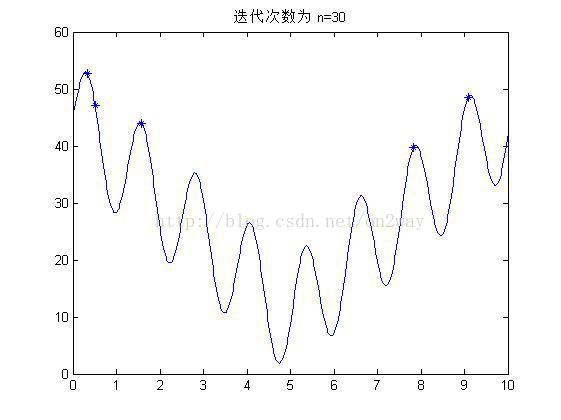
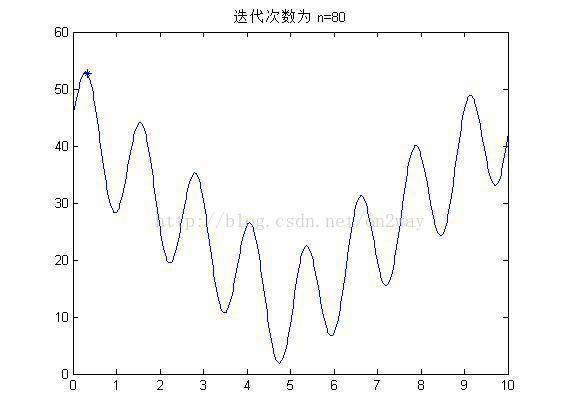
      if  mod(i,10)==0

      figure;

      

      fplot('10*sin(5*x)+7*abs(x-5)+10',[0 10]);

      hold on;

      title(['迭代次数为 n=' num2str(i)]);

      plot(x1,y1,'*');

      end

  end

      fprintf('the best X is  --->>%5.2f\n',x2);

      fprintf('the best Y is  --->>%5.2f\n',bestfit);

%-------------函数说明----------------

%    初始化种群大小

%       输入变量：

%               popsize:种群大小

%               chromlength：染色体长度--》转化的二进制长度

%       输出变量：

%               pop：种群

%---------------------------------------

function pop = initpop(popsize,chromlength)

pop = round(rand(popsize,chromlength));

 

%-------------函数说明----------------

%     二进制转化十进制函数

%       输入变量：

%               二进制种群

%       输出变量：

%               十进制数值

%---------------------------------------

function pop2 = binary2decimal(pop)

[px,py]=size(pop);

for i=1:py

    pop1(:,i) = 2.^(py-i).*pop(:,i);

end

%sum(.,2)对行求和，得到列的向量

temp = sum(pop1,2);

pop2 = temp*10/1023;

 

%-------------函数说明----------------

%     计算函数目标值

%       输入变量：

%              二进制数值 

%       输出变量：

%               目标函数值

%---------------------------------------

function [objvalue]=cal_objvalue(pop)

x = binary2decimal(pop);

%转化二进制数为x变量的变化域范围的数值

% x = temp*10/1023;

% objvalue = 10*sin(5*x)+7*cos(4*x);

% objvalue = 10*sin(x)+7*x+10

objvalue = 10*sin(5*x)+7*abs(x-5)+10;

 

%-------------函数说明----------------

%      

%       输入变量：

%                pop  ：  二进制种群

%                fitvalue  ：  适应度值

%       输出变量：

%                newpop：选择以后的二进制种群

%---------------------------------------

function [newpop] = selection(pop,fitvalue)

%构造轮盘

[px,py]=size(pop);

totalfit = sum(fitvalue);

p_fitvalue = fitvalue/totalfit; 

p_fitvalue = cumsum(p_fitvalue);%概率求和排序

%-------

ms = sort(rand(px,1));%从小到大排列

fitin = 1;

newin = 1;

while newin<=px

     if (ms(newin))<p_fitvalue(fitin)

         newpop(newin,:)=pop(fitin,:);

         newin=newin+1;

     else fitin=fitin+1;

     end

 end

 

%-------------函数说明----------------

%      

%       输入变量：

%             pop:二进制的父代种群数

%             pc：交叉的概率

%       输出变量：

%             newpop：交叉后的种群数   

%---------------------------------------

function [newpop]=crossover(pop,pc)

[px,py]=size(pop);

newpop = ones(size(pop));

for i=1:2:px-1

    if(rand<pc)

        cpoint = round(rand*py);

        newpop(i,:) = [pop(i,1:cpoint),pop(i+1,cpoint+1:py)];

        newpop(i+1,:) = [pop(i+1,1:cpoint),pop(i,cpoint+1:py)];

    else

        newpop(i,:)=pop(i,:);

        newpop(i+1,:)=pop(i+1,:);

    end

end

 

%-------------函数说明----------------

%      

%       输入变量：

%                 pop  ：  二进制种群

%                 pm  ：  变异概率

%       输出变量：

%                newpop  ：  变异以后的种群

%---------------------------------------

function [newpop] = mutation(pop,pm)

[px,py] = size(pop);

newpop = ones(size(pop));

for i=1:px

    if(rand<pm)

        mpoint = round(rand*py);

        if mpoint<=0

            mpoint=1;

        end

        newpop(i,:) = pop(i,:);

        if newpop(i,mpoint)==0

            newpop(i,mpoint)=1;

        else newpop(i,mpoint)=0;

        end

    else

        newpop(i,:)=pop(i,:);

    end

end

 

%-------------函数说明----------------

%      

%       输入变量：  

%                pop  :  种群

%                fitvalue  ：  种群适应度 

%

%       输出变量：

%                bestindividual  ： 最佳个体（二进制个体）

%                bestfit     ：   最佳适应度值

%---------------------------------------

function [bestindividual,bestfit]=best(pop,fitvalue)

[px,py]=size(pop);

bestindividual = pop(1,:);

bestfit = fitvalue(1);

for i=2:px

    if fitvalue(i)>bestfit

        bestindividual = pop(i,:);

        bestfit = fitvalue(i);

    end

end

（2）实验结果