原理:
----------------------------------------------------------------------------------------------------
给定n个权值作为n个叶子结点,构建一棵二叉树,若带权值路径长度达到最小,称这样的二叉树为哈夫曼树。
Huffman树是一种特殊的二叉树,其叶结点的编码是一种前缀码,同时,通过统计字符的频度,能够达到编码电文的最小化。
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。n个权值分别设为w1、w2、···、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、···、wn看成有n棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3) 将新树加入森林中;
(4) 重复(2)、(3)步,直到森林中的树都被比较过为止,该树即为所求得的哈夫曼树。
实现步骤:
----------------------------------------------------------------------------------------------------
1.建立哈夫曼树前先根据权值对结点进行从小到大的排序1...n;
2.哈夫曼树的总结点数为2*n-1,新节点下标从n+1到2*n-1新节点从小到大产生;
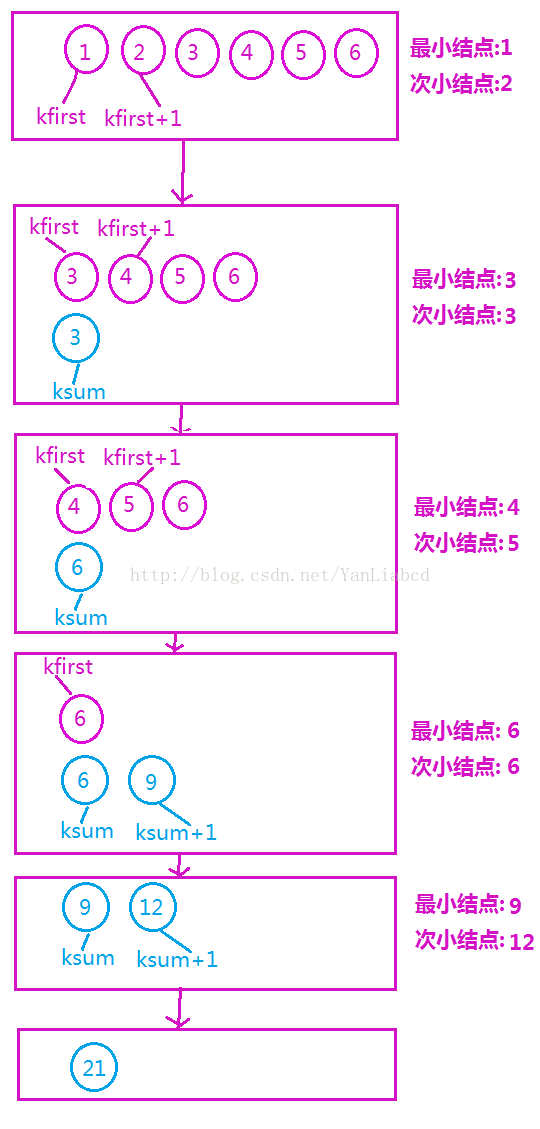
3.最小结点和次小结点在旧结点未加入树里的最小两个结点和新结点未被加入到树里的最小的两个结点总共四个结点中产生;设置旧结点未加入树里的最小结点的下标为kfirst,新节点未被加入到树里的最小结点的下标为ksum:
(1)当产生第一个新结点即下标为n+1的结点时,最小结点和次小结点的下标分别是1和2;
(2)当产生第二个新结点即下标为n+2的结点时,最小结点和次小结点的下标在3,4和n+1中产生;
(3)当产生新结点的下标大于n+2时,最小结点和次小结点的下标在kfirst,kfirst+1和ksum,ksum+1中产生;
画图显示蓝色表示新节点,红色表示旧结点:
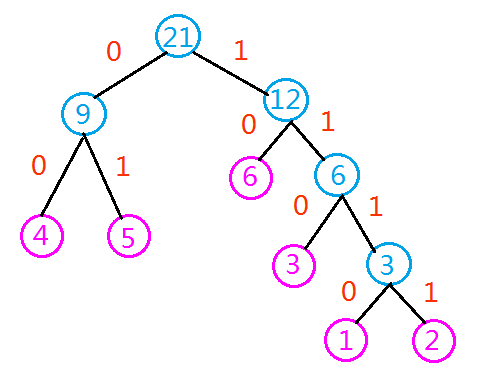
总流程图,红色表示旧结点:
C语言代码:
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<string.h>
typedef struct{
unsigned int weight;//权值
unsigned int parent, lchild,rchild;//父结点,左孩子,右孩子
}HTNode,*HuffmanTree;
typedef char ** HuffmanCode;
//旧结点根据权值由小到大排序
int sort(HuffmanTree t,int n)
{
int i,j,k;
for(i=1;i<n;i++){
for(j=1;j<=n-i;j++)
if(t[j].weight>t[j+1].weight)
{
k=t[j].weight;
t[j].weight=t[j+1].weight;
t[j+1].weight=k;
}
}
return 1;
}
//找出未被加入树里的最小结点和次小结点下标
int Select(HuffmanTree HT,int n,int *s1,int *s2,int i,int &kfirst,int &ksum)
{
if(i==n+1)
{
*s1=1;
*s2=2;
kfirst=3;
ksum=n+1;
}
else{
int b[4]={0,0,0,0};
int index[4];
int ii,j;
//把旧结点中未加入树中的最小和次小值加到b数组中
for(j=0, ii=kfirst;ii<kfirst+2&&ii<=n&&j<4;ii++,j++){
b[j]=HT[ii].weight;
index[j]=ii;
}
//把新结点中未加入树中的最小和次小值加到b数组中
for(j=j, ii=ksum;ii<ksum+2&&ii<=i-1&&j<4;ii++,j++){
b[j]=HT[ii].weight;
index[j]=ii;
}
//把最小值和次小值得下标分别放到index[0]和index[1]中
for(int aa=0;aa<2;aa++){
if(aa==0){
for(int k=1;k<4&&b[k]>0;k++){
if(b[0]>b[k]){
int temp=b[0];
int subtemp=index[0];
b[0]=b[k];
index[0]=index[k];
b[k]=temp;
index[k]=subtemp;
}
}
}
else{
for(int k=2;k<4&&b[k]>0;k++){
if(b[1]>b[k]){
int temp=b[1];
int subtemp=index[1];
b[1]=b[k];
index[1]=index[k];
b[k]=temp;
index[k]=subtemp;
}
}
}
}
*s1=index[0];
*s2=index[1];
//找出旧结点中未加入到树中的最小结点对应的下标kfirst和新结点中未加入到树中的最小结点对应的下标ksum
if(index[1]==kfirst+1&&kfirst+2<=n){
kfirst=kfirst+2;
}else if(index[1]==ksum+1&&ksum+2<=2*n-1){
ksum=ksum+2;
}
else{
kfirst=kfirst+1;
ksum=ksum+1;
}
}
return 1;
}
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n,int &kfirst,int &ksum)
{
int i,m,s1,s2,start;
char *cd;
unsigned int c,f;
if(n<=1) exit(1);
m=2*n-1;
for(i=n+1;i<=m;i++)
{
HT[i].parent=0;
}
//产生新节点
for(i=n+1;i<=m;i++)
{
Select(HT,n,&s1,&s2, i,kfirst,ksum);
HT[s1].parent=i;HT[s2].parent=i;
HT[i].lchild=s1;HT[i].rchild=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
HC=(HuffmanCode )malloc((n+1)*sizeof(char* ));
cd=(char *)malloc(n*sizeof(char ));
cd[n-1]='\0';
for(i=1;i<=n;i++)
{
HC[i]=(char*)malloc((n-start)*sizeof(char));
start=n-1;
for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)
{
if(HT[f].lchild==c)
{
cd[--start]='0';
}
else
{
cd[--start]='1';
}
strcpy(HC[i],&cd[start]);
}
}
free(cd);
}
void main()
{
HuffmanTree HT;
HuffmanCode HC;
int *w,n,j,K;
int i,m,s1,s2;//i为结点的下标,m为总结点数,s1为最小结点下标,s2为次小结点的下标
int kfirst=0,ksum=0;//旧结点未加入树里的最小结点的下标kfirst,新节点未被加入到树里的最小结点的下标ksum:
HuffmanTree p;
char *cd;
printf("结点的个数为:\n");
scanf("%d",&n);
w=(int *)malloc(n*sizeof(int));
for(i=1;i<=n;i++)
{
printf("第%d个结点的权值为:",i);
scanf("%d",w+i-1);
}
if(n<=1) exit(1);
m=2*n-1;//总结点数
HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
for(i=1;i<=n;i++,w++)
{
HT[i].weight=*w;
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
sort(HT, n);
HuffmanCoding(HT,HC,w, n,kfirst,ksum);
for(i=1;i<=n;i++)
{
printf("权值为%d结点的哈夫曼编码:",HT[i].weight);
puts(HC[i]);
}
for(i=1;i<=n;i++)
free(HC[i]);
free(HC);
free(HT);
}运行结果:
Java代码:
<pre name="code" class="java">package c;
import java.util.Scanner;
//结点类
class HTNode {
int weight;
int parent, lchild, rchild;
}
public class HuffmanDemo {
static int[] s = new int[3];
static int kfirst = 1;//旧结点未加入树里的最小结点的下标kfirst
static int ksum;//新节点未被加入到树里的最小结点的下标ksum:
public static void main(String[] args) {
HuffmanDemo hf = new HuffmanDemo();
int n;
System.out.println("结点的个数为:");
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
ksum = n + 1;
HTNode[] HT = new HTNode[2 * n];
for (int i = 0; i <= 2 * n - 1; i++) {
HT[i] = new HTNode();
}
hf.input(n, HT);
StringBuilder[] HC = new StringBuilder[n + 1];
hf.sort(HT, n);
StringBuilder[] hcret;
hcret = hf.HuffmanCoding(HT, HC, n);
for (int i = 1; i <= n; i++) {
System.out.print("权值为" + HT[i].weight + "结点的哈夫曼编码:");
System.out.println(hcret[i].reverse());
}
}
// 输入结点权值
void input(int n, HTNode[] HT) {
Scanner sc = new Scanner(System.in);
int[] w = new int[20];
int i;
for (i = 1; i <= n; i++) {
System.out.println("第" + i + "个结点的权值为:");
w[i] = sc.nextInt();
}
if (n <= 1)
System.exit(1);
for (i = 1; i <= n; i++) {
HT[i].weight = w[i];
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
}
// 结点根据权值由小到大排序
int sort(HTNode[] t, int n) {
int i, j, k;
for (i = 1; i < n; i++)
for (j = 1; j <= n - i; j++)
if (t[j].weight > t[j + 1].weight) {
k = t[j].weight;
t[j].weight = t[j + 1].weight;
t[j + 1].weight = k;
}
return 1;
}
// 找出未被加入树里的最小结点和次小结点下标
public int[] Select(HTNode[] HT, int n, int[] s, int i) {
if (i == n + 1) {
s[1] = 1;
s[2] = 2;
kfirst = 3;
ksum = n + 1;
} else {
int b[] = { 0, 0, 0, 0 };
int index[] = new int[4];
int ii, j;
// 把旧结点中未加入树中的最小和次小值加到b数组中
for (j = 0, ii = kfirst; ii < kfirst + 2 && ii <= n && j < 4; ii++, j++) {
b[j] = HT[ii].weight;
index[j] = ii;
}
// 把新结点中未加入树中的最小和次小值加到b数组中
for (ii = ksum, j = j; ii < ksum + 2 && ii <= i - 1 && j < 4; ii++, j++) {
b[j] = HT[ii].weight;
index[j] = ii;
}
// 把最小值和次小值得下标分别放到index[0]和index[1]中
for (int aa = 0; aa < 2; aa++) {
if (aa == 0) {
for (int k = 1; k < 4 && b[k] > 0; k++) {
if (b[0] > b[k]) {
int temp = b[0];
int subtemp = index[0];
b[0] = b[k];
index[0] = index[k];
b[k] = temp;
index[k] = subtemp;
}
}
} else {
for (int k = 2; k < 4 && b[k] > 0; k++) {
if (b[1] > b[k]) {
int temp = b[1];
int subtemp = index[1];
b[1] = b[k];
index[1] = index[k];
b[k] = temp;
index[k] = subtemp;
}
}
}
}
s[1] = index[0];
s[2] = index[1];
// 找出旧结点中未加入到树中的最小结点对应的下标kfirst和新结点中未加入到树中的最小结点对应的下标ksum
if (index[1] == kfirst + 1 && kfirst + 2 <= n) {
kfirst = kfirst + 2;
} else if (index[1] == ksum + 1 && ksum + 2 <= 2 * n - 1) {
ksum = ksum + 2;
} else {
kfirst = kfirst + 1;
ksum = ksum + 1;
}
}
return s;
}
// 编码
StringBuilder[] HuffmanCoding(HTNode[] HT, StringBuilder[] HC, int n) {
int i, m, start;
char[] cd = new char[100];
int c, f;
if (n <= 1)
System.exit(1);
m = 2 * n - 1;
for (i = n + 1; i <= m; i++) {
HT[i].parent = 0;
}
for (i = n + 1; i <= m; i++) {
int[] ss = new int[3];
int[] sa = new int[3];
sa = Select(HT, n, ss, i);
HT[sa[1]].parent = i;
HT[sa[2]].parent = i;
HT[i].lchild = sa[1];
HT[i].rchild = sa[2];
HT[i].weight = HT[sa[1]].weight + HT[sa[2]].weight;
}
cd[n - 1] = '\0';
for (i = 1; i <= n; i++) {
HC[i] = new StringBuilder();
start = n - 1;
for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent) {
if (HT[f].lchild == c) {
cd[--start] = '0';
} else {
cd[--start] = '1';
}
HC[i].append((char) cd[start]);
}
}
return HC;
}
}
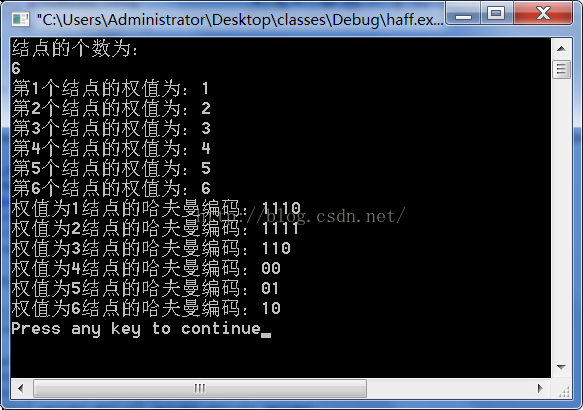
运行结果:


























 3847
3847

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








