HDU 1560 DNA sequence（IDA*）

DNA sequence

Time Limit: 15000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2666    Accepted Submission(s): 1299

Problem Description

The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

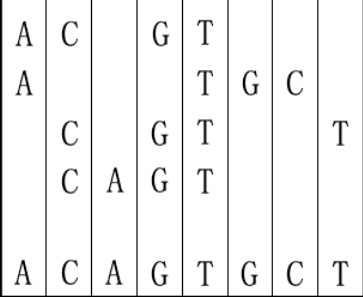
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

 

Input

The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

 

Output

For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

 

Sample Input

  
  

   
   1
4
ACGT
ATGC
CGTT
CAGT
  
  

 

Sample Output

  
  

   
   8
  
  

 

Author

LL

 

Source

HDU 2006-12 Programming Contest 

 

Recommend

LL

题目大意：

    给你几个字符串，按照如图所示方法合并，求最小长度。

解题思路：

    首先计算一下，状态数比较多，而且hash的效果不是很好，就考虑不用bfs。然后发现估值函数很好写，就可以用A*了，又是求最小值，就可以用IDA*了。

AC代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define mem(a,b) memset((a),(b),sizeof(a))

const int MAXN=8+3;
const int MAXL=5+3;
const char dna[]={'A','T','C','G'};

int N,len[MAXN],now[MAXN],deep;
char s[MAXN][MAXL];

bool fal()//检查是否到达终态
{
    for(int i=0;i<N;++i)
        if(now[i]!=len[i])
            return false;
    return true;
}

bool a_star(int l)//估值函数
{
    int the_max=0;
    for(int i=0;i<N;++i)
        the_max=max(the_max,len[i]-now[i]);
    return l+the_max>deep;
}

bool dfs(int l)
{
    if(a_star(l))//利用A*剪枝
        return false;
    if(fal())//到达终态
        return true;
    for(int i=0;i<4;++i)
    {
        bool upd[MAXN]={0};//保存状态，用来回溯
        char c=dna[i];
        bool have=false;
        for(int j=0;j<N;++j)
            if(s[j][now[j]]==c)
            {
                have=true;
                upd[j]=true;
                ++now[j];
            }
        if(have)
        {
            if(dfs(l+1))
                return true;
            for(int j=0;j<N;++j)//回溯
                if(upd[j])
                    --now[j];
        }
    }
    return false;
}

int main()
{
    int T_T;
    scanf("%d",&T_T);
    while(T_T--)
    {
        scanf("%d",&N);
        for(int i=0;i<N;++i)
        {
            scanf("%s",s[i]);
            len[i]=(int)strlen(s[i]);
        }
        deep=1;
        while(true)//不断加深深度
        {
            for(int i=0;i<N;++i)
                now[i]=0;
            if(dfs(0))
            {
                printf("%d\n",deep);
                break;
            }
            else ++deep;
        }
    }
    
    return 0;
}