洛谷P1240 诸侯安置 递推

题目大意：有一片正方形状（旋转45°看）的国土，有m个诸侯需要安置。诸侯在同一行或同一列上会互相伤害0.0，求出合理安置诸侯（使诸侯两两之间都不能攻击）的方案数对504取模的结果。(n≤100，k≤2n2-2n+1)

这张图中上面第一幅图为n=3的国土分布。下面前两幅图中两个诸侯会互相攻击，而第三幅图不会

看到这道题首先想到八皇后问题，但是n<=100，dfs会爆炸T_T。于是想到递推，但是对于这样一个菱形的国土也没有什么好的递推顺序，需要转化成更加“规则”的图形。

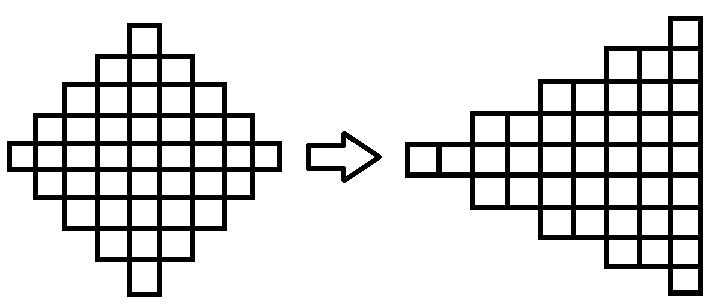
这样转化不会影响到最终结果，并且为递推提供了一个可行的顺序。
设f[i][j]表示前i列里安置了j个诸侯且第i列安置了诸侯的方案数，那么有
F[i][j]=sigma{f[k][j-1]*(col[i]-(j-1))} 其中 j-1<= k < i
col[i] 表示第i列有几行，在第i列之前已经放置了j-1个诸侯，也就是在第i列有j-1行不能放置诸侯，那么在第i列就有(col[i]-(j-1))个位置是可行的。
答案即为ans=sigma{f[i][m]} 其中k<=i<=n*2-1

#include <cstdio>
using namespace std;
int n,m,ans;
int col[210],f[210][210];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) col[i*2-1]=col[i*2]=i*2-1;
    if(m>n*2-2) ans=0;
    else {
        f[0][0]=1;
        for(int i=1;i<=n*2-1;i++)
            for(int j=1;j<=i;j++)
                for(int k=j-1;k<i;k++)
                    f[i][j]=(f[i][j]+f[k][j-1]*(col[i]-j+1))%504;
        for(int i=m;i<=n*2-1;i++) ans+=f[i][m];
    }
    printf("%d\n",ans%504);
    return 0;
}