【最优化】对偶函数

Yoki_Niu

于 2023-12-20 22:43:30 发布

阅读量287

点赞数 1

文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/Yoki_Niu/article/details/135101800

版权

最近在狂补数学，想着还是需要一点输出来加深一下理解。浅浅做一个学习记录，如有错误或疏漏之处，还望大家批评指正。

一、对偶函数

1. 拉格朗日函数的引入：对于一个无约束优化问题，可以对目标函数直接进行求导，找到函数的极值点。而对于有约束的优化问题，该方法不可行，因为优化变量的取值范围很大程度上受到约束条件的限制，优化变量不一定能取到一阶导数的零点位置。因此将约束条件也考虑进目标函数中，得到增广的目标函数。该转换的好处是，新的目标函数不存在约束条件，优化变量可以取到整个定义域。

2. 标准优化问题形式：

$minimize \, f_{0}\left ( x \right )\: \: \:s.t.\, f_{i}\left ( x \right )\leq 0,\: h_{i}(x)=0$

拉格朗日函数：

$L(x,\lambda ,\nu )=f_{0}(x)+\sum \lambda _{i}f_{i}(x)+\sum \nu _{i}h_{i}(x)$

3. 对拉格朗日函数取关于x的最小值，得到拉格朗日对偶函数。对于任意λ≥0，拉格朗日对偶函数构成了原问题最优解的下界：

$g(\lambda ,\nu )=inf\: L(x,\lambda ,\nu )=inf(f_{0}(x)+\sum \lambda_{i}f_{i}(x)+\sum \nu_{i}h_{i}(x))\leqslant p^{*}$

证明：假设x*为x的一个可行解，p*为最优解

$\lambda\geq 0, f_{i}(x^*)\leq 0,h_{i}(x^*)=0$

$\rightarrow \sum \lambda_{i} f_{i}(x)+\sum \nu_{i} h_{i}(x)\leq 0$

$\rightarrow g(\lambda,\nu)\leq L(x^*,\lambda,\nu)\leq f_{0}(x^*)$

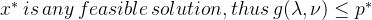
$x^* \: is\, any\, feasible\, solution, thus\, g(\lambda,\nu)\leq p^*$

说明：对偶函数是关于λ和v的线性函数，线性函数既为凸函数又为凹函数。由于inf运算具有保凹性，因此将对偶函数视为凹函数。凹函数具有唯一的极大值。

二、对偶函数与共轭函数的关系

1. 共轭函数： $f(y^*)=sup(y^Tx-f(x))$

2. 优化问题： $minimize \, f_{0}\left ( x \right )\: \: \:s.t.\, Ax\leq b,\: Cx=d$

3. 对偶函数：

$g(\lambda,\nu)=inf(f_{0}(x)+\lambda^T(Ax-b)+\nu ^T(Cx-d))$

$=-b^T\lambda-d^T\nu+inf(f_{0}(x)+(A^T\lambda+C^T\nu)^Tx)$

$=-b^T\lambda-d^T\nu-f_{0}^*(-A^T\lambda-C^T\nu)$

由于共轭函数与对偶函数存在上述关系，因此可以通过求解对偶函数进而求得共轭函数，共轭函数求解本质上也是拉格朗日乘子法的应用之一！

三、强对偶与弱对偶 / slater条件

1. 对偶问题的描述：由上述分析可知，对偶函数构成了原问题最优值的下界，又因为对偶函数为凹函数，具有唯一的极大值。因此很自然就能想到，如果能够找到对偶函数的最大值，则可以获得关于最优值最好的下界。因此对偶问题可以表述为：

$maximize\, \, g(\lambda,\nu)\, \, \, \, s.t.\, \lambda\succeq 0$

将上述求解得到的对偶函数的最优值记作d*，易得d*≤p*。

2. d*≤p*在任何条件下都成立，因为在上述推导过程中，我们并未对函数进行任何限制，该性质称为弱对偶性。p*-d*表示原问题最优值与对偶函数所能获得最好下界的差值，称为最优对偶间隙。

3. 在某些特殊情况下，d*恰好与p*相等，此时我们所求得的对偶函数的最优值即为原问题的最优解，这种情况称为强对偶。那么什么时候才能获得强对偶呢？除了要求原问题为凸问题，还需要一些其他的约束准则。

4. Slater条件：存在至少一点x，使得所有不等约束条件严格成立，即：

$\exists \, x\in relint\, D, so\, that\, f_{i}(x)< 0,\, Ax=b$

说明：若不等约束函数fi中有部分仿射函数，则条件可适当放宽，仿射不等约束函数只需满足小于等于0即可，其余约束函数仍需满足严格小于0。

因此，若一个问题为凸问题，且满足Slater条件，则该问题具有强对偶性。

强弱对偶性的几何解释：

为简单起见，考虑仅含有一个不等约束的优化问题

原问题为： $minimize \, f_{0}\left ( x \right )\: \: \:s.t.\, f_{i}\left ( x \right )\leq 0$

令： $t=f_{0}(x), u=f_{i}(x),G={(f_{0}(x),f_{i}(x)|\exists x\in D)}$

原问题的最优解即为G中 $f_{0}(x)$ 的最小值。

又由于 $u=f_{i}(x)\leq 0$ ，所以最优解 $p^*$ 如图所示：

对偶问题可表述为： $g(\lambda)=inf(t+\lambda u),\, \, (u,t)\subseteq G$

由于 $t+\lambda u$ 为一个线性函数，因此在该直线上 $g(\lambda)$ 的值处处相等。

若令 $u=0$ ，则截距 $t$ 即为 $g(\lambda)$ 的值。

在图中任意改变斜率 $-\lambda(\lambda> 0)$ ，可发现图中所有的 $g(\lambda)$ 都小于 $p^*$ ，并且在红色直线处，可以得到 $g(\lambda)$ 的最大值，即最优解 $d^*$ 。由此，弱对偶性可证。

如何将弱对偶转换成强对偶呢？

我们发现，可以将图中的两点连接起来，使其形成一个凸集，则 $p^*=d^*$

因此，对于绝大数凸问题而言，它们天然满足强对偶性。

然而对于如图所示的凸问题，它无法满足强对偶性。因此，我们增加了slater约束准则，要求直线 $t+\lambda u$ 必须是非竖直的，它必须穿过点 $(u,t)=(f_{0}(x),f_{i}(x))$ 的左侧。

四、KKT条件

1. 若原问题和对偶问题的最优值都可以达到并且相等（强对偶性成立），则存在互补松驰性：

$\sum \lambda_{i}^{*}f_{i}(x^*)=0$

等价条件：

$\lambda_{i}^{*}> 0\rightarrow f_{i}(x^*)=0$

$f_{i}(x^*)< 0 \rightarrow \lambda_{i}^{*}=0$

证明：

假设 $x^*$ 为原问题的最优解， $(\lambda^*, \nu^*)$ 为对偶最优解。

$f_{0}(x^*)=g(\lambda^*, \nu^*)$

$=inf(f_{0}(x)+\sum \lambda _{i}f_{i}(x)+\sum \nu _{i}h_{i}(x))$

$\leq f_{0}(x^*)+\sum \lambda _{i}^{*}f_{i}(x^*)+\sum \nu _{i}^{*}h_{i}(x^*)$

$\leq f_{0}(x^*)$

第一个等式说明对偶间隙为0；
第二个等式为对偶函数的定义；
第三个不等式是根据对偶函数是由拉格朗日函数关于x取下确界所得到的；
第四个不等式是根据 $\lambda^*\geq 0, f_{i}(x^*)\leq 0,h_{i}(x^*)=0$ 得到的。因此，在上述关系链中，两个不等号都必须取等号才能满足条件。由此可推出： $\sum \lambda_{i}^{*}f_{i}(x^*)=0$

2. KKT最优性条件：

假设不等约束和等式约束函数均为可微函数：

$f_{i}(x^*)\leq 0$
$h_{i}(x^*)=0$
$\lambda^*\geq 0$
$\lambda_{i}^{*}f_{i}(x^*)=0$
$\bigtriangledown f_{0}(x^*)+\sum\lambda_{i}^{*}\bigtriangledown f_{i}(x^*)+\sum\nu_{i}^{*}\bigtriangledown h_{i}(x^*)=0$

说明：若原问题为非凸问题，KKT最优性条件为必要条件；若原问题为凸问题，则KKT条件为充要条件。

证明：

前两个条件说明了 $x^*$ 是原问题的可行解。
第三个条件是最优值下界存在的前提条件。
第四个条件为强对偶性成立，则存在松弛互补性。
第五个条件说明拉格朗日函数在 $x^*$ 处取得极值，即：

$g(\lambda ^*,\nu ^*)=L(x^*,\lambda^* ,\nu^* )$

$=f_{0}(x^*)+\sum\lambda_{i}^{*}f_{i}(x^*)+\sum\nu_{i}^{*}h_{i}(x^*)$

$\because h_{i}(x^*)=0, \lambda_{i}^{*}f_{i}(x^*)=0$

$\therefore g(\lambda ^*,\nu ^*)=f_{0}(x^*)$