Saddleback Search

Saddleback Search

从leetcode看到，具体可见链接
下面是自己的理解和翻译。

设有一待查找的数x和一个二维数组b[0..m-1, 0..n-1]（均为整数），每行和每列都是非降序（等于升序？），例子如下，此时m=4，n=4：

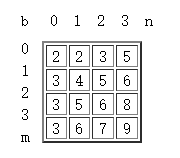
这里的x假设一定存在于b中，该算法就是从数组b中找到x的位置，因此有条件：
Q： x 存在于b[0..m-1, 0..n-1]中
该算法将结果存于变量h和k中，即：
R： x=b[h,k].

//以下是思考过程（或者废话，可跳过）：
首先需要一个循环或递归过程，这里选择循环，然后需要一个循环不变量，这个循环不变量产生于R和Q，为了得出不变量，注意到R可以写成和Q一样的形式，即：
R： x存在于b[h..h,k..k]
Q是说x在一个大的范围内，R是说x在一个小的范围内，也许这个循环不变量P应该说x在一个范围内。重新按R的格式写这个不变量，并且用两个新的变量表示范围：
不变量P： x存在于b[h..i, j..k]（这里有意思了，这里潜在的意思是行是从右往左找，列是从上往下找）
于是这个算法就非常简单了，它在最差的情况下运行时间为O(m+n)，需要注意和利用的是一开始的条件，该数组，每行和每列都是非降序，即已经排好序了。
//思考过程完毕（废话完毕）

该算法简而言之是这样的：
1.从右上角开始找，即从b[0,n-1]开始找
【注：h,k=0,n-1, P: x存在于b[h..m-1, 0..k]中】
2.如果x大于b[h,k]，那么h=h+1
3.如果x小于b[h,k]，那么k=k-1
4.如果x匹配，那么返回h和k的值，即为所要查找的位置

注：以上算法并没有考虑x有重复多个值的情况或者x不存在的情况，仅限于x存在于b并且找到一个下标即可。

附leetcode 240 Search a 2D Matrix II code：

python:

class Solution(object):
    def searchMatrix(self, matrix, target):
        """
        :type matrix: List[List[int]]
        :type target: int
        :rtype: bool
        """
        if not len(matrix) or not len(matrix[0]): return False
        n,m,c=0,len(matrix[0])-1,len(matrix)
        while(n<c and m>=0):
            if matrix[n][m]>target: m-=1
            elif matrix[n][m]<target: n+=1
            else: return True
        return False

C++:

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size()==0) return false;
        int n=0,m=matrix[0].size()-1,c=matrix.size();
        while(n<c && m>=0){
            if(matrix[n][m]>target) m-=1;
            else if(matrix[n][m]<target) n+=1;
            else return true;
        }
        return false;
    }
};

纪念第一篇博客诞生撒花~~~~