使用 GeoDa 软件进行空间自相关分析
双击打开 GeoDa 软件
选择 .shp 文件

导入文件
 空间权重矩阵(*.gal / *.gwt)是进行任何空间分析的前提
空间权重矩阵(*.gal / *.gwt)是进行任何空间分析的前提
构建空间权重矩阵
空间权重矩阵(Spatial Weights Matrix) 是一个用来描述空间对象之间相互关系的矩阵。
它反映了地理单位之间“邻接”或“距离接近”关系,是进行空间计量分析的基础。
空间权重矩阵是一个用来表示地理单元之间“谁和谁是邻居”的表格,它决定了你在进行空间分析时,哪些单元会被当作“周围环境”来计算
定义空间邻居关系


点---基于距离
 Arc Distance基于球面经纬度,考虑地球曲率
Arc Distance基于球面经纬度,考虑地球曲率
中文名称 说明 使用场景 Euclidean Distance 欧氏距离 最常见的直线距离计算方法,即“勾股定理”形式,单位与坐标系统一致。
例如: √[(x₂ - x₁)² + (y₂ - y₁)²]坐标为投影坐标(如米、千米),一般城市区域或栅格数据分析 Arc Distance
(mi)
弧线距离(英里) 基于地球球面模型计算两地之间的球面弧线距离,单位为英里 全球或跨区域分析,使用经纬度坐标数据 Arc Distance
(km)
弧线距离(千米) 同上,单位为千米 全球范围分析,常用于交通、气候空间数据分析

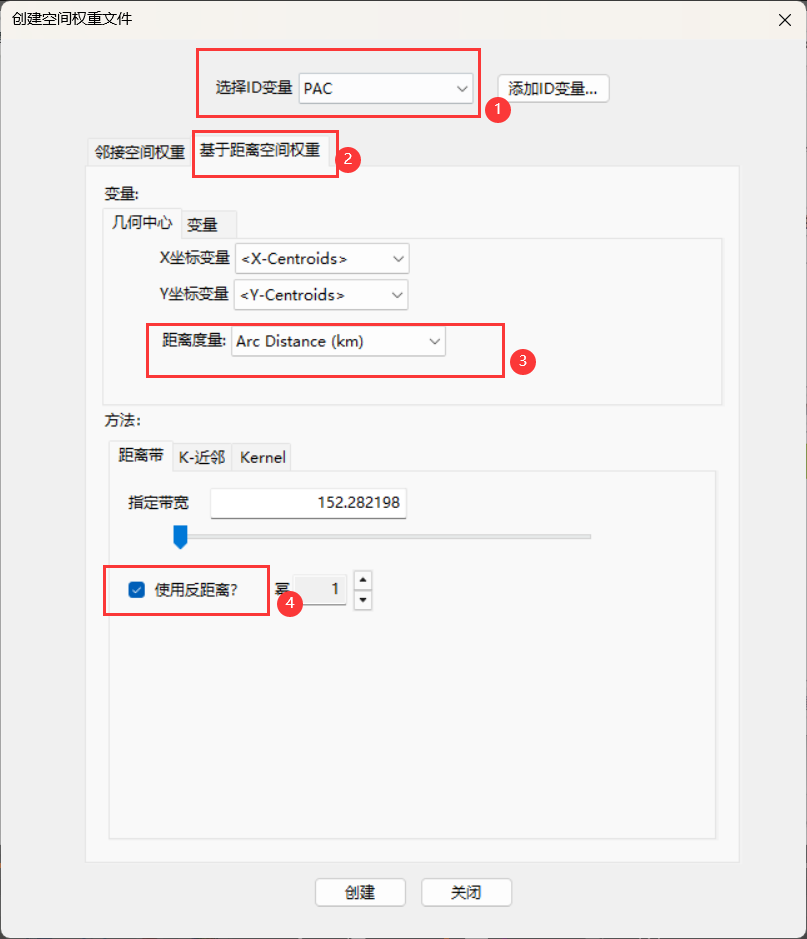
点击创建,选择保存的文件位置

创建成功后就可以关闭了
全局空间自相关
在菜单栏点击:
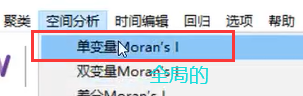
选择你想分析的变量(如:CI)
勾选使用的权重矩阵(默认的话会自动使用)

点击 ,软件会生成:

Moran’s I 值
Z-score 和 p 值(显著性)
散点图(Moran Scatter Plot)
📌 结果解读:
Moran’s I > 0:正自相关(聚集)
Moran’s I < 0:负自相关(离散)
Z 值越大,p 值越小 → 空间聚集越显著
局部空间自相关
菜单栏点击:

同样选择你分析的变量
使用默认的空间权重矩阵

 点击 输出内容:
点击 输出内容:

红色:High-High 聚集(热点)
蓝色:Low-Low 聚集(冷点)
粉红:High-Low(高值被低值包围)
浅蓝:Low-High(低值被高值包围)
灰色:不显著区域(p > 0.05)
选中高亮的数量

shift和鼠标配合
右下角可以看到选中数量
![]()












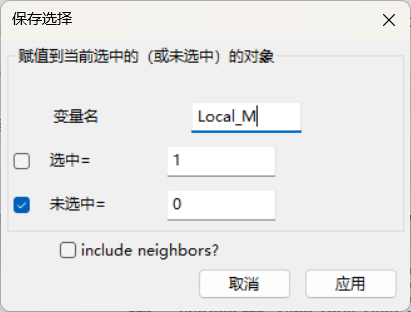

上面4步还要重做一下
点击保存,设置好后


空间权重矩阵(Spatial Weight Matrix)是空间计量分析和空间数据建模中的核心工具,用来描述一个空间单元(比如一个区域、城市、网格等)与其他空间单元之间的“相邻”或“关联”关系
空间权重矩阵是一个 n × n 的矩阵,n 表示空间单元的数量,矩阵中的每一个元素 wij表示第 i 个单元与第 j 个单元之间的空间关系强度。
-
如果 wij=1,表示 i 与 jj是邻居;
-
如果 wij=0,表示两者不是邻居;
-
更复杂的形式中,wij可以是两个单元之间的距离的函数,比如反比距离 wij=1/dij
常见构建方法
邻接矩阵(Binary contiguity matrix)
-
仅表示是否相邻,常见的有:
-
Rook 邻接:四邻域(上下左右相邻才算邻居);
-
Queen 邻接:八邻域(包括对角线)
-
距离衰减矩阵(Distance-based weight)
根据单元之间的实际距离构建,距离越远,权重越小
 一般 α=1 或 2;d是距离
一般 α=1 或 2;d是距离
距离阈值:超出距离就设为 0
准化权重矩阵
对每一行做归一化,

可以防止单位之间邻居数量不一致带来的影响

























 8290
8290

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










