Linear regression with one variable

1.Promble:

       In this part of this exercise, you will implement linear regression with one variable to predict profits for a food truck. Suppose you are the CEO of a restaurant franchise and are considering different cities for opening a new outlet. The chain already has trucks in various cities and you have data for profits and populations from the cities.
       You would like to use this data to help you select which city to expand to next.

       The file ex1data1.txt contains the dataset for our linear regression problem. The first column is the population of a city and the second column is the profit of a food truck in that city. A negative value for profit indicates a loss.

2.Computing the cost J(θ):

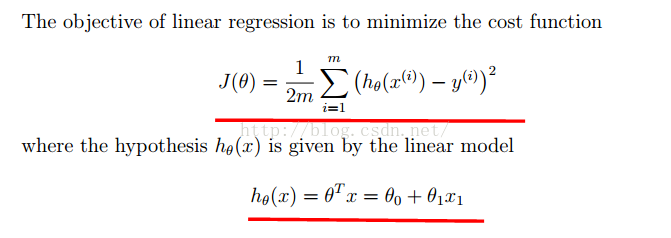
此部分matlab代码如下：

<span style="font-size:14px;">function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y
 
% Initialize some useful values
m = length(y); % number of training examples
 
% You need to return the following variables correctly 
J = 0;
 
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
J = sum((X * theta - y).^2) / (2*m);     % X(79,2)  theta(2,1)</span>
 
end

3.Gradient Descent&Update Equations

此部分matlab代码如下：

<span style="font-size:14px;">function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha
 
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s=theta;
 
for iter = 1:num_iters
 
    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);       
    theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));   
    theta_s=theta; 
    
 
    % ============================================================
 
    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);
 
end
J_history
end</span>

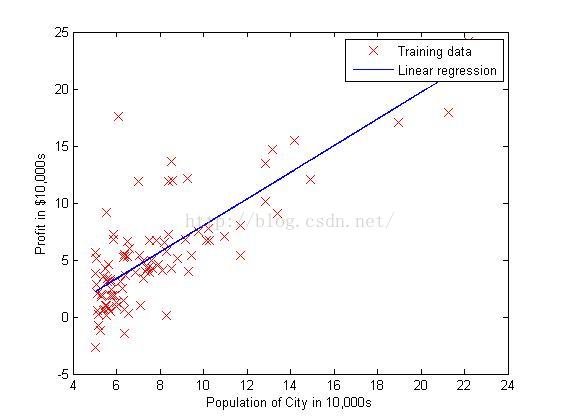
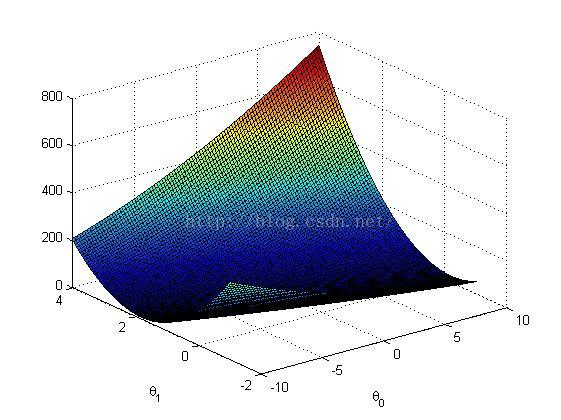
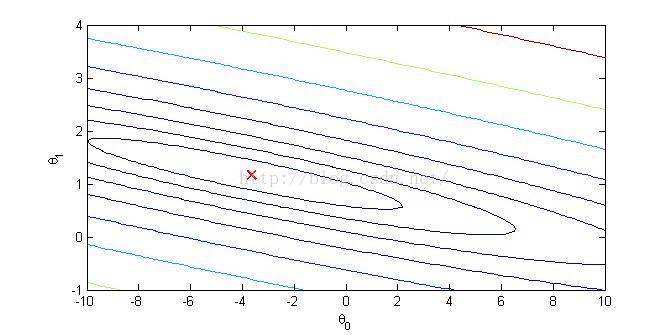
最终程序运行结果如下：

整个程序的代码见：http://download.csdn.net/detail/zhe123zhe123zhe123/9535946