前言:
因为自己理不清机器学习的一些分布,所以无法和其他大佬一样给出一个很好的框架,
只能根据个人的学习进度去更新。
其中大部分概念来源于课程,其余的图和一些公式来自于其他大佬的博客中,
因为自己不是很会处理图,难免有借鉴但无抄袭之意
(一)Linear Regression with one variable (单变量线性回归)
(1)回归问题属于机器学习中的监督问题,且给出一系列点假设拟合直线为h(x)=θ0+θ1*x,(这里有可能是多维)
这里因为是单变量线性回归问题,所以变量属性只是一维。
(2)该方法的核心思想是从离散的统计数据中得到数学模型,然后将该数学模型用于预测或者分类。该方法处理的数据可以是多维的。
(3)这其实就是小学or初中知识吧,y = kx + b ; 且要求尽可能多的包含点画出一条平滑曲线(直线);
问题引入:(图片引用于jerrylead大佬的机器学习笔记,资料来源于百度文库)
这是一个XXX地的房价表格,现在将它在二维坐标轴上表达出来
当我们获得了新的数据集时候,就需要在在这个坐标轴上添加新的点,但是并无相关规律or记录去表达它的和适度。这时候就需要拟合出一条(上面说的小学知识)尽可能涵盖所有点的曲线来让他们呈现出一种规律,这样造出一条直线就可以将新加入的点的对应值返回了。
这期间涉及部分概念,下面列出:
(1)包含房子面积和价格的数据集称为训练集training set
(2)输入变量x(本例中为面积)为特征features
(3)输出的预测值y(本例中为房价)为目标值target
(4)拟合的曲线,一般表示为y = h(x),称为假设模型hypothesis
(5)训练集的条目数称为特征的维数
所以由上述概念可以引出本问题的这几个参数表:
Cost function : 刚开始可能不理解这个 Cost Function的函数, 其实就是我们要拟合出一条接近完美的曲线,而越完美的曲线则与标准曲线在误差越小;这里平方要会将误差缩的更小,1/2是为了未来求导的时候把系数消除掉,而求和是整体曲线的误差。
Goal : 就要目标,要求得函数J的最小值。
二、如何调整θ让J(θ)保持最小值
(1)梯度下降法:
在选定线性回归模型后,只需要确定参数 θ,就可以将模型用来预测。然而 θ 需要在 J(θ) 最小的情况下才能确定。因此问题归结为求极小值问题,使用梯度下降法。梯度下降法最大 的问题是求得有可能是全局极小值,这与初始点的选取有关。
梯度下降法是按下面的流程进行的: 1)首先对 θ 赋值,这个值可以是随机的,也可以让 θ 是一个全零的向量。 2)改变 θ 的值,使得 J(θ)按梯度下降的方向进行减少。
梯度方向由 J(θ)对 θ 的偏导数确定,由于求的是极小值,因此梯度方向是偏导数的反方向。 结果为
迭代更新的方式有两种,一种是批梯度下降,也就是对全部的训练数据求得误差后再对 θ 进行更新,另外一种是增量梯度下降,每扫描一步都要对 θ 进行更新。前一种方法能够不断 收敛,后一种方法结果可能不断在收敛处徘徊。
一般来说,梯度下降法收敛速度还是比较慢的。感觉和贪心思想差不多,并不能保证全局最优
(2)最小二乘法
可能对这两种算法的理解还不是很透彻,先放在这里,未来仍旧需要多学习学习











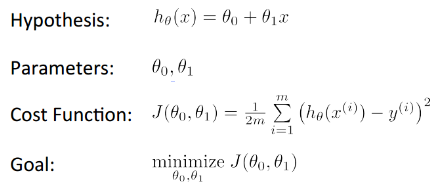


















 1615
1615

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










