【NOIP2016提高A组集训第13场11.11】最大匹配

题意

现在给你一个N个点N-1条边的连通图，希望你能够求出这个图的最大匹配以及最大匹配的数量。
两个匹配不同当且仅当存在一条边在第一个匹配中存在而在第二个匹配中不存在。
N<=100000

第一行两个数T,P,其中T表示数据组数。
接下来每组数据第一行一个数N
接下来N-1行每行两个数分别表示一条边。

对于每组数据，输出一行：
若p=1，则一行一个数输出图的最大匹配
若p=2，则一行两个数输出图的最大匹配以及最大匹配数量，答案对10^9+7取模。

题解

Hungary
我们先观察一下这道题的一些性质。首先它是一棵树，然后对于P=1时，我们可以发现，对于一颗以x为根子树而言，我们只需要关注x是否已经和儿子匹配，和整颗子树匹配了多少。那么我们设计对于P=1的算法的时候，只需要注意少数状态就可以了，那么这样很容易用DP实现。先设1为根。
设F[x][0,1]表示以x为根的子树，x匹配了或者没匹配的情况下，最大匹配数。
再设son集合，表示x的儿子。
那么递推式明显：

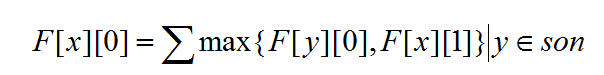
还有

那么P=1就在O(n)复杂度内解决了。
现在我们再来思考P=2中多出来的求方案数怎么办。很明显，假如转移中需要取max的元素有多个，即有多个最大值的话，那么他们组合在一起，算不同方案嘛。按照F的式子容易推出G的。
设G[x][0,1]，表示当前状态下，最大匹配的方案数。
那么：

G[x][1]的式子:

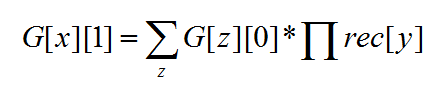
Y定义同上。Z为F[x][1]取值最大时的那些Z。
解释：
若在不同z的情况下F[x][1]都一样，G[x][1]就要把对于不同z的方案数都加起来。因为取不同z都可以有当前状态下的最大匹配，取每个都有若干的方案数，显然加起来嘛。
那么最后最大匹配就是max(f[1][0],f[1][1])，方案数类似G[x][0]的统计方法。

说说实现上的问题，在我的方法中：G[x][1]的式子中你可以用G[x][0]除掉rec[z]再乘G[z][0]，这时候涉及模意义下的除法，用费马小定理，求出ref[z]逆元，可以实现。当然还有别的优秀方法。

代码

#include<cstdio>
#include<algorithm>
using namespace std;
#define fo(i,j,k) for(i=j;i<=k;i++)
typedef long long ll;
const int N=200005;
const int mo=1000000007;
int f[N][2],f1,f0,rec[N],b[N],next[N],first[N],tt,i,j,n,x,y,T,P;
int g[N][2],g0;
void cr(int x,int y)
{
    tt++;
    b[tt]=y;
    next[tt]=first[x];
    first[x]=tt;
}
int ksm(int x,int y)
{
    if (!y) return 1;
    if (y==1) return x;
    int dur=ksm(x,y/2);
    return (ll)dur*dur%mo*ksm(x,y%2)%mo;
}
int inv(int x)
{
    return ksm(x,mo-2);
}
void dfs1(int x,int y)
{
    g[x][0]=g[x][1]=1;
    if (!next[first[x]]) g[x][1]=0;
    f[x][1]=f[x][0]=0;
    int p;
    for(p=first[x];p;p=next[p])
    if (b[p]!=y)
    {
        dfs1(b[p],x);
        f0=f[b[p]][0];
        f1=f[b[p]][1];
        f[x][0]+=max(f0,f1);
        if (f0>f1)
        {
            g[x][0]=(ll)g[x][0]*g[b[p]][0]%mo;
            rec[b[p]]=g[b[p]][0];
        }
        else if (f0<f1)
        {
            g[x][0]=(ll)g[x][0]*g[b[p]][1]%mo;
            rec[b[p]]=g[b[p]][1];
        }
        else
        {
            g[x][0]=(ll)g[x][0]*(g[b[p]][1]+g[b[p]][0])%mo;
            rec[b[p]]=(g[b[p]][1]+g[b[p]][0])%mo;
        }
    }
    for(p=first[x];p;p=next[p])
    if (b[p]!=y)
    {
        f0=f[x][0]-max(f[b[p]][0],f[b[p]][1])+f[b[p]][0]+1;
        g0=(ll)g[x][0]*inv(rec[b[p]])%mo*g[b[p]][0]%mo;
        if (f[x][1]<f0)
            g[x][1]=g0;
        else if (f[x][1]==f0) 
            (g[x][1]+=g0)%=mo;
        f[x][1]=max(f[x][1],f0);
    }
}
int main()
{
    freopen("hungary.in","r",stdin);
    freopen("hungary.out","w",stdout);
    scanf("%d %d",&T,&P);
    while (T--)
    {
        tt=0;
        fo(i,1,n) first[i]=0;
        scanf("%d",&n);
        fo(i,1,n-1)
        {
            scanf("%d %d",&x,&y);
            cr(x,y);
            cr(y,x);
        }
        dfs1(1,0);
        if (P==1)
        {
            printf("%d\n",max(f[1][0],f[1][1]));
        }
        else
        {
            printf("%d ",max(f[1][0],f[1][1]));
            if (f[1][0]==f[1][1])
                printf("%d\n",(g[1][0]+g[1][1])%mo);
            else if (f[1][0]>f[1][1])
                printf("%d\n",g[1][0]);
            else
                printf("%d\n",g[1][1]);
        }
    }
    fclose(stdin);
    fclose(stdout);
}