题目描述

分析
结论:任意一条路径的异或和,都可以看做是一条固定的简单路径的xor和,再xor若干个环的xor和。
怎么思考呢?我们可以先把环走掉。从s出发,走到环上,把环走一遍,然后再回到s,这样,我们得到了这个环的xor值,也回到了s;把环走掉,然后再走简单路径。
那为什么固定一条简单路径就行了呢?假设有多条简单路径到t,由于是无向图,肯定有些包含s或者包含t的环,那么把固定的简单路径的异或值xor上这些环,就能得到其他的简单路径。
那么我们现在要把所有的环xor值找出来。显然,把每个环都找出来是不现实的,我们需要用到线性基。
一个大环可以看做是若干个小环的线性组合,如果我们维护了小环的线性基,那么大环显然不用找嘛。所以dfs跑一遍图,对于返祖边(u,v),我们把u到v的树路径的异或和xor上这条边的边权,插入线性基即可。
好了,我们现在有了一条简单路径,和环的线性基,怎么算答案呢?
按位考虑,考虑第i位,设简单路径xor和为temp,我们计算有多少种temp和线性基的线性组合能让第i位是1的方案。思路是:xor上0是不会改变原来的值的;如果temp这一位为1,它要异或上偶数个1,如果为0,要异或上奇数个1;我求的时候用了比较麻烦的方法,实际上不需要。
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
typedef double db;
#define fo(i,j,k) for(i=j;i<=k;i++)
#define fd(i,j,k) for(i=j;i>=k;i--)
const int N=2e5+5,W=60,mo=1e9+7;
int tt,first[N],next[N],b[N],pp[N],dfn[N],low[N],pd[N],in[N],dft,sta[N],ts,n,m,i,j,x,y,st,en,siz,ans,fac[W+5],rev[W+5],cnt,tp;
ll c[N],base[100],xsum[N],tmp,two[W+5],tw[W+5],z,dur;
void cr(int x,int y,ll z)
{
tt++;
b[tt]=y;
c[tt]=z;
next[tt]=first[x];
first[x]=tt;
}
void insert(ll x)
{
int i,j;
fd(i,W,0)
if (x&tw[i])
{
if (base[i])
{
x^=base[i];
if (!x) return;
}
else
{
base[i]=x;
fd(j,i-1,0) if (base[j]&&(base[i]&tw[j])) base[i]^=base[j];
fo(j,i+1,W) if (base[j]&tw[i]) base[j]^=base[i];
break;
}
}
}
void tarjan(int x)
{
++dft;
low[x]=dfn[x]=dft;
in[x]=1;
sta[++ts]=x;
for(int p=first[x];p;p=next[p])
if (!pp[(p-1)/2+1])
{
pp[(p-1)/2+1]=1;
if (!dfn[b[p]])
{
xsum[b[p]]=xsum[x]^c[p];
tarjan(b[p]);
low[x]=min(low[x],low[b[p]]);
}
else if (in[b[p]]!=2)
{
insert(xsum[x]^xsum[b[p]]^c[p]);
low[x]=min(low[x],dfn[b[p]]);
}
}
if (low[x]==dfn[x])
while (sta[ts+1]!=x)
in[sta[ts--]]=2;
}
int ksm(int x,int y)
{
int ret=1;
while (y)
{
if (y&1) ret=1ll*ret*x%mo;
x=1ll*x*x%mo;
y>>=1;
}
return ret;
}
void predo()
{
two[0]=1;
tw[0]=1;
fo(i,1,W) two[i]=two[i-1]*2%mo,tw[i]=tw[i-1]*2;
fac[0]=1;
fo(i,1,W) fac[i]=1ll*fac[i-1]*i%mo;
rev[W]=ksm(fac[W],mo-2);
fd(i,W,1) rev[i-1]=1ll*rev[i]*i%mo;
}
int comb(int n,int m)
{
return 1ll*fac[m]*rev[n]%mo*rev[m-n]%mo;
}
int main()
{
freopen("xor.in","r",stdin);
freopen("xor.out","w",stdout);
scanf("%d %d",&n,&m);
fo(i,1,m)
{
scanf("%d %d %lld",&x,&y,&z);
cr(x,y,z);
cr(y,x,z);
}
scanf("%d %d",&st,&en);
predo();
tarjan(st);
tmp=xsum[en];
fo(i,0,W) if (base[i]) siz++;
fo(i,0,W)
{
cnt=0;
fo(j,i,W) if ((base[j]>>i)&1) cnt++;
tp=0;
for(j=((tmp<<i)&1)^1;j<=cnt;j+=2)
tp=(tp+comb(j,cnt))%mo;
ans=(ans+1ll*tp*two[siz-cnt]%mo*two[i])%mo;
}
printf("%d\n",ans);
}







 通过分析,任意路径的异或和可看作简单路径异或和与环的异或和的组合。使用线性基处理环,通过DFS获取环的线性组合,最后结合简单路径计算答案。重点在于理解和应用线性基解决图论问题。
通过分析,任意路径的异或和可看作简单路径异或和与环的异或和的组合。使用线性基处理环,通过DFS获取环的线性组合,最后结合简单路径计算答案。重点在于理解和应用线性基解决图论问题。
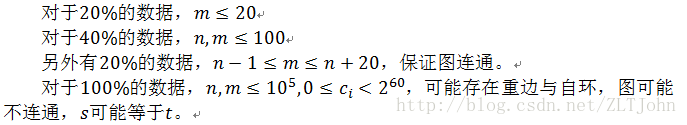














 399
399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








