365天读文献，Day4，含空位缺陷石墨烯的铜基纳米复合材料

由于石墨烯薄片中不可避免的原子空位缺陷，石墨烯增强纳米复合材料的热弹性性能显著降低。由于现有的微观力学模型无法有效捕捉空位缺陷的影响，因此准确预测这些纳米复合材料的机械性能成为一项巨大挑战。本文基于分子动力学（MD）数据库和遗传编程（GP）算法，提出了一种数据驱动的建模方法，解决了这一关键问题，并利用该方法修改现有的Halpin-Tsai模型和混合规则，考虑空位缺陷的影响。数据驱动的微观力学模型能够在不同温度下，提供石墨烯增强铜（Cu）纳米复合材料的热弹性性能的准确高效预测，且其决定系数（R²）均大于0.9。此外，经过充分训练的数据驱动微观力学模型还被应用于功能梯度缺陷石墨烯增强复合材料梁的热屈曲、弹性屈曲、自由振动和静态弯曲分析，并进行了详细的参数研究，重点分析了缺陷百分比、石墨烯含量、分布模式及温度对结构行为的影响。

Background（背景）

石墨烯因其超高的弹性模量和强度，成为理想的轻质高强度复合材料增强材料。尽管已有研究（如Kim等人）通过透射电子显微镜和分子动力学（MD）模拟验证了金属-石墨烯复合材料的机械性能提升，但这些研究通常忽略了石墨烯缺陷对复合材料强化效果的影响。石墨烯在生长或加工中不可避免的缺陷会调节其局部性能，并改善石墨烯与基体的界面粘结，从而影响复合材料的机械性能。

目前，热弹性性能多通过Halpin-Tsai模型和混合规则进行预测，但这些模型仅考虑了石墨烯含量和尺寸，忽略了缺陷和温度等因素，限制了其工程应用。因此，修改现有微观力学模型显得尤为重要。

近年来，机器学习（ML）技术在材料科学中应用广泛，通过训练大规模数据集来预测复合材料的性能。如人工神经网络和支持向量机等算法在材料性能预测中表现出较强的预测能力，但由于缺乏明确的数学表达式，常被视为“黑箱”模型。相比之下，遗传编程（GP）作为一种能推导输入输出关系的技术，已成功应用于工程系统材料性能预测。本文基于遗传编程方法，修正Halpin-Tsai模型和混合规则，预测缺陷石墨烯增强纳米复合材料的热弹性性能。

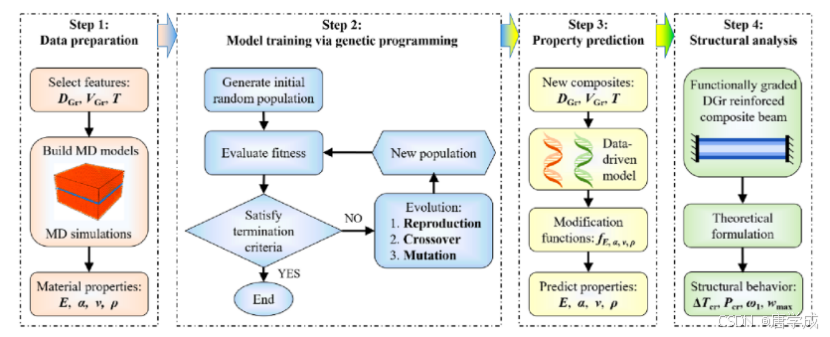
石墨烯增强复合材料已应用于功能梯度结构，以提升结构性能。然而，现有模型未考虑石墨烯缺陷和温度的影响。本文开发了数据驱动模型，预测空位缺陷石墨烯增强铜（Cu）纳米复合材料的热弹性性能。通过遗传编程算法训练MD模拟数据集，得到明确的表达式，修正现有微观力学模型，并验证其与实验和模拟结果的一致性。最后，利用这些模型分析功能梯度缺陷石墨烯增强复合材料梁的结构行为。

Methods and models（方法与模型）

1、模型

缺陷率（Dr）

石墨烯重量分数（WGr）

石墨烯的体积分数（VGr）

2、遗传编程（GP）

3、评估

Results and discussion（结果与讨论）

1、缺陷石墨烯增强纳米复合材料的热弹性性能

石墨烯缺陷的影响：随着石墨烯缺陷百分比的增加，杨氏模量逐渐下降，从0%缺陷（155.44 GPa）下降到1%缺陷（149.89 GPa），减少约3.57%。缺陷使石墨烯的刚度降低，进而降低了复合材料的机械性能。然而，石墨烯缺陷对热膨胀系数（CTE）、泊松比和密度的影响较小。

石墨烯含量的影响：随着石墨烯含量的增加，杨氏模量显著提高，14.47 vol%时为149.89 GPa，比2.95 vol%时增加86.04%。同时，CTE大幅下降，石墨烯含量为14.47 vol%时，CTE减少了约32.63%。此外，较高的石墨烯含量使复合材料的密度降低，便于设计轻质高强度材料。

温度的影响：随着温度升高，复合材料的杨氏模量下降，密度减小，但CTE和泊松比上升，这与温度引起的原子热振动增加相关。

2、基于MD仿真和GP算法的数据驱动建模

2.1、训练得到修正公式

2.2、结果评估

本文通过数据驱动模型与分子动力学（MD）模拟结果的对比，验证了缺陷石墨烯增强复合材料的热弹性性能。例如，数据驱动的Halpin–Tsai模型预测的杨氏模量的均方根误差（RMSE）分别为1.99%、1.75%和1.88%，R²值分别为0.9311、0.9385和0.9471，表明该模型能够准确捕捉缺陷百分比、石墨烯含量和温度等输入变量对杨氏模量的影响。此外，数据驱动的混合规则模型也能准确预测其他热弹性性能，如热膨胀系数和泊松比，其RMSE低于3%，R²值高于0.9，进一步验证了模型的准确性和有效性。在计算效率方面，数据驱动模型相较于MD模拟具有显著优势，预测时间仅为1分钟，而MD模拟平均需20个CPU小时，显著降低了计算成本。

除了遗传编程（GP）算法，本文还评估了KNN、决策树（DT）和随机森林（RF）等其他机器学习方法用于预测缺陷石墨烯增强铜纳米复合材料的材料性能。尽管这些方法也能准确估算材料性能，并且具有高R²值，但与GP算法不同的是，它们无法生成输入与输出之间的明确数学表达式。因此，本文选择使用遗传编程（GP）算法来开发微观力学模型。

2.3、数据驱动模型的验证

通过与现有的实验和模拟数据对比，验证了数据驱动微观力学模型的泛化能力（图7）

3、功能梯度缺陷石墨烯增强复合材料梁的力学行为

图8展示了一种细长的多层（NL）缺陷石墨烯增强复合材料梁，其厚度为h，长度为L，宽度为b，其中缺陷石墨烯在每层内均匀分布，且石墨烯含量沿厚度方向逐层变化。每层假设为各向同性且均匀的，厚度为h/NL。设计了三种不同的缺陷石墨烯分布模式（见图8），其中颜色较深表示石墨烯含量较高。模式U-WGr是一个特殊情况，即各层石墨烯含量相同的各向同性均匀梁。模式X-WGr和O-WGr则是对称分布，其中X-WGr梁的表面层石墨烯含量最大，而O-WGr梁则相反，表面层石墨烯含量最小。

通过将现有的数值解与本理论公式的分析解进行比较，验证了当前的理论公式。表3比较了C-C石墨烯增强复合材料梁的临界屈曲温度变化、无量纲临界屈曲载荷、无量纲基频和无量纲最大挠度，与文献[22, 24, 26, 29]中的结果。示例中使用的材料属性可以在这些文献中找到。原始的Halpin–Tsai模型用于评估石墨烯增强复合材料的材料参数。从表中可以看出，分析结果与现有结果高度一致，验证了理论公式的有效性。

对具有功能梯度的缺陷石墨烯增强复合梁的热屈曲、弹性屈曲、自由振动和静态弯曲行为进行分析。考虑的复合梁共有 10 层，长宽比为 60，每一层由石墨烯/铜（Cu）复合材料制成，且包含空位缺陷。分析四个量：热屈曲ΔTcr、弹性屈曲pcr、自由振动ω1和静态弯曲ωmax

3.1、热屈曲

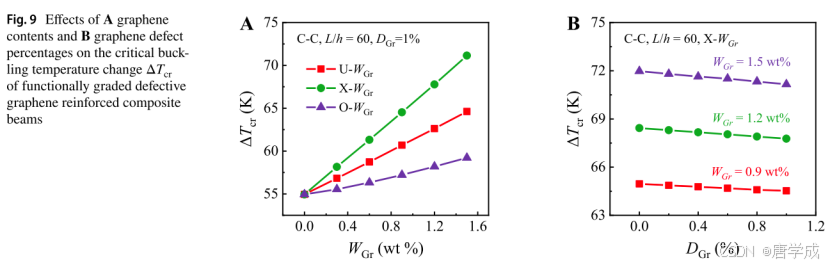
图 9 比较了不同石墨烯含量和缺陷百分比的功能梯度缺陷石墨烯增强复合梁的热屈曲行为。图 9A 显示，具有 X-WGr 分布模式的复合梁能够承受比其他两种石墨烯分布模式更高的热载荷。这是因为 X-WGr 梁中更多的石墨烯分布在靠近表面层，达到了最高的梁刚度。因此，所有功能梯度缺陷石墨烯增强复合梁的临界屈曲温度随着石墨烯含量的增加而增加。以 X-WGr 梁为例，当石墨烯含量为 1.5 wt% 时，临界屈曲温度的变化量 ΔTcr约为 71.15 K，比纯铜梁大约高出 29.50%。

图 9B 研究了石墨烯缺陷对 X-WGr 缺陷石墨烯增强复合梁临界屈曲温度的影响。随着石墨烯缺陷百分比的增加ΔTcr从约 71.98 K（无缺陷石墨烯增强复合梁）降至约 71.15 K（缺陷百分比为 1% 的石墨烯增强复合梁），减少了约 1.15%。这是因为石墨烯缺陷的增加导致石墨烯及其复合材料的性能退化，从而降低了复合材料的力学性能。

3.2、弹性屈曲

图 10 展示了不同石墨烯含量、缺陷百分比和温度下复合梁的弹性屈曲响应。从图 10A 可以看出，随着石墨烯含量的增加，所有 U-WGr、X-WGr 和 O-WGr 梁的临界屈曲载荷pcr均有所增加，其中 X-WGr 梁表现出最大的屈曲抗力。对于 X-WGr（1.5 wt%）梁，屈曲载荷增加了约 37.29%。

图 10B 显示，随着石墨烯缺陷百分比的增加，临界屈曲载荷pcr逐渐下降。当 X-WGr 梁的石墨烯含量为 1.5 wt% 时，缺陷百分比从 0.0 增加到 1.0%，屈曲载荷减少了约 3.49%。

图 10C 显示，温度对临界屈曲载荷也有负面影响，当温度从 300 K 增加到 400 K 时，屈曲载荷减少了约 1.05%。

3.3、自由振动特性

图 11 展示了不同石墨烯含量、缺陷百分比和温度下复合梁的自由振动特性。石墨烯嵌入金属基体中越多，石墨烯/铜复合材料的刚度越大，从而导致复合梁的基本固有频率增加。图 11A 显示，三种石墨烯分布模式中，X-WGr 梁具有最大的基本固有频率，约为 0.1515，当石墨烯含量为 1.5 wt% 时。另一方面，石墨烯中的空位缺陷降低了石墨烯及其复合材料的性能，导致复合梁的基本固有频率下降（图 11B）。

随着温度从 300 K 增加到 400 K，复合梁的基本固有频率也显著下降（图 11C）。

3.4、静态弯曲

图 12 展示了不同石墨烯含量、缺陷百分比和温度下，功能梯度缺陷石墨烯增强复合梁在横向均匀载荷作用下的静态弯曲行为。随着石墨烯含量的增加，每个复合梁的最大挠度静态弯曲ωmax都逐渐减小，因为石墨烯的加入有效地提高了铜基复合材料的刚度。以 X-WGr 梁为例，当石墨烯含量为 1.5 wt% 时，静态弯曲ωmax下降了约 27.14%。

然而，随着石墨烯中缺陷的增加，梁的灵活性提高，导致弯曲变形增大（图 12B）。图 12C 显示，梁暴露在高温下时，最大挠度进一步增加。

Conclusions（结论）

本研究基于分子动力学（MD）模拟和遗传编程（GP）算法，成功开发了数据驱动的微观力学模型，用于预测不同温度条件下的缺陷石墨烯/Cu 纳米复合材料的热弹性性能。模拟结果表明，在300 K下，14.47 vol% 石墨烯含量的复合材料的杨氏模量可以在缺陷百分比从0.0%到1.0%变化时，在约155.44 GPa和149.89 GPa之间进行有效调节。我们收集了包括杨氏模量、热膨胀系数（CTE）、泊松比和密度等热弹性性能，以及石墨烯缺陷百分比、石墨烯含量和温度等关键特征，使用GP算法进行模型训练。这些数据驱动的微观力学模型具有较高的预测精度，R²值大于0.9，均方根误差（RMSE）低于3%。

此外，本研究还探讨了功能梯度缺陷石墨烯增强复合材料梁的热屈曲、弹性屈曲、自由振动和静态弯曲行为。分析中使用的材料参数来自数据驱动的Halpin–Tsai模型和混合规则。结果表明，石墨烯主要分布在表面层的复合梁表现出更好的承载能力，并且随着石墨烯含量的增加，承载能力进一步提高。另一方面，石墨烯中的缺陷对复合梁的结构行为有一定的负面影响。此外，结果还显示，高温条件下梁的结构刚度会下降，导致热屈曲、弹性屈曲、自由振动和静态弯曲性能降低。