CINTA第三次作业

CINTA第三次作业

第六章7、8、9、10

---

7、设G是群，对任意n∈N，i∈[0,n] ，∈G。的逆元是...。

证明：由群公理封闭性得   ∵ ∈G  ∴ ∈G

           根据公理：任意a∈G，存在逆元∈G，使得 ；

           ∵（）·（...）

              =

              =e

                

              =

              =e

          ∴ 的逆元是...。

---

8、证明：任意群G的两个子群的交集也是群G的子集。 

证明：设 、  是群G的两个子群

           任意a、b∈ 、 

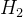
           根据群公理封闭性得：∈ 、∈

           ∴ a、b∈∩

           满足群公理封闭性

           ∴ 任意群G的两个子群的交集也是群G的子集

---

9、证明或伪证：任意群G的两个子群的并集也是群G的子集。

证明： 设 、  是群G的两个子群

            任意 a∈ 且 a∉、任意b∈ 且b∉

            ∴∉ 、∉

            ∴∉∪

            不满足群公理封闭性

            ∴任意群G的两个子群的并集也是群G的子集

---

10、G是阿贝尔群，H和K是G的子群。请证明HK={hk：h∈H，k∈K}是群G的子群 。如果G不是阿贝尔群，结论是否仍然成立？

证明：取任意、∈H ，、∈K

          ∴ ∈HK   ∈HK

          ∵ H和K是G的子群

          ∴ 、、、 ∈ G

          由封闭性得：∈G 、 ∈G 、 ∈G

          ∵ G是阿贝尔群

          ∴  = 

          ∵ ∈H 、∈K

          ∴ ∈HK

          即 ∈HK

          满足封闭性 ∴ HK={hk：h∈H，k∈K}是群G的子群

          若G不是阿贝尔群，其不满足交换律 ∴ 结论不成立

---