数列分块总结

于 2023-02-02 17:30:31 发布
阅读量477 收藏
点赞数
分类专栏： 数据结构 文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/ZhuRanCheng/article/details/128854390
版权

数列分块

一、基本思想

分块是一种思想，即把一个整体分成若干个小块，对整块整体处理，对临散块单独处理；

数列分块即为一种利用分块思想处理数列区间问题的一种数据结构；

数列分块具体思想如下图所示，

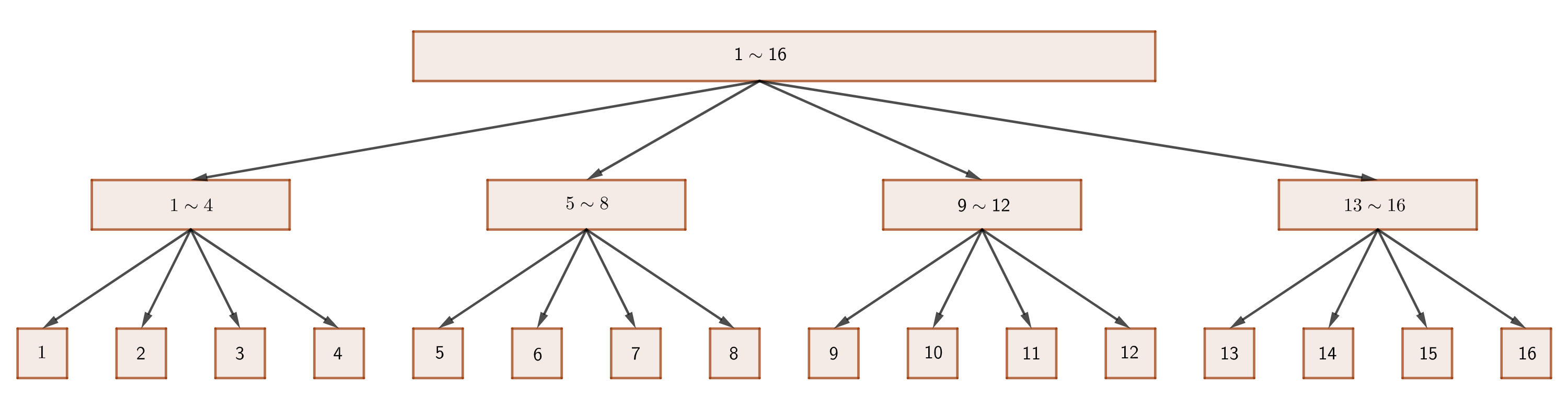
数列分块基本思想

将一个长度为 n n n 数组划分为 a a a 块，每块长度为 n a \frac{n}{a} an​ ，则对于一个区间操作，首先对区间内的完整块进行整块操作，再对区间边缘的临散块进行暴力处理；

对于整块的修改可直接更新整块的总值，在查询时再将整块的修改向下传递到块内每个元素中；

关于 a a a 的取值，若 a a a 太小，则区间中整块的数量会少，需要大量时间处理零散块；若 a a a 太大，又会让块的长度太短，失去整体处理的意义，所以为了平衡块内与块间的运算时间，通常使 a = n a = \sqrt n a=n ​ ，则数列分块总时间复杂度为 O ( n ) O(\sqrt n) O(n ​) ；

二、基本操作

1. 预处理

思路

预处理可处理出每个块的左右端点，块内元素和以及每个元素所对应的块的编号；

t t t 为块的个数， a a a 为原数组， s u m i sum_i sumi​ 为第 i i i 个块内元素的总和， a d d i add_i addi​ 为第 i i i 个块的修改标记， L i ， R i L_i， R_i Li​，Ri​ 分别为第 i i i 个块的维护左右下标， p o s i pos_i posi​ 表示下标为 i i i 的元素所属块的编号；

代码
int t, a[MAXN], sum[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	t = sqrt(n * 1.0); // 块的个数
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1; // 块的左端点
		R[i] = i * t; // 块的右端点
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n; // 若有剩余，新加一个块
	for (int i = 1; i <= t; i++) { // 遍历每个块
		for (int j = L[i]; j <= R[i]; j++) { // 遍历块内元素
			pos[j] = i; // 数组元素对应的分块
			sum[i] += a[j]; // 计算初始块内和
		}
	}
}

2. 区间修改

思路

对于一个区间 [ l , r ] [l, r] [l,r] 将区间内值全部加 d d d 的修改；

首先先判断两个端点 l l l 与 r r r 是否在同一个块里，若在相同块内即可直接暴力修改；

否则则暴力修改两端零散的点，以及点所属的块内总和；

再修改整块，修改块的标记及总和，但不修改元素值，在最终查询时再将标记向块内的元素传递；

代码
void change(int l, int r, int d) {
	int p = pos[l], q = pos[r]; // 获取查询端点所属块
	if (p == q) { // 两个点在同一块当中
		for (int i = l; i <= r; i++) a[i] += d; // 暴力修改
		sum[p] += d * (r - l + 1); // 更新块内元素和
	} else {
		for (int i = p + 1; i <= q - 1; i++) add[i] += d; // 更新整块标记
		for (int i = l; i <= R[p]; i++) a[i] += d; // 暴力更新左端零散的元素
		sum[p] += d * (R[p] - l + 1); // 更新块内元素和
		for (int i = L[q]; i <= r; i++) a[i] += d; // 暴力更新右端零散的元素
		sum[q] += d * (r - L[q] + 1); // 更新块内元素和
	}
}

3. 单点查询

思路

单点查询即直接用元素原值加上其所属块的标记即可；

代码
int query(int i) {
	return a[i] + add[pos[i]]; // 元素原值加上其所属块的标记
}

4. 区间查询

思路

对于查询区间 [ l , r ] [l, r] [l,r] 的和；

首先先判断两个端点 l l l 与 r r r 是否在同一个块里，若在相同块内即可直接暴力求和，但注意最后还应加上其所属块的标记；

否则则暴力求两端零散的点的和加上其所属块的标记；

再查询整块即用原块内和加上块的标记查询即可；

代码
int ask(int l, int r) {
	int p = pos[l], q = pos[r]; // 获取查询端点所属块
	int ans = 0;
	if (p == q) { // 两个点在同一块当中
		for (int i = l; i <= r; i++) ans += a[i]; // 将查询区间的元素类加进答案
		ans += add[p] * (r - l + 1); // 加上修改标记
	} else {
		for (int i = p + 1; i <= q - 1; i++) ans += sum[i] + add[i] * (R[i] - L[i] + 1); // 原块内和加上块的标记
		for (int i = l; i <= R[p]; i++) ans += a[i]; // 累加左端零散的元素
		ans += add[p] * (R[p] - l + 1); // 加上修改标记
		for (int i = L[q]; i <= r; i++) ans += a[i]; // 累加右端零散的元素
		ans += add[q] * (r - L[q] + 1); // 加上修改标记
	}
	return ans; // 返回查询结果
}

三、数列分块入门 9 题

数列分块入门 1

题目

区间加法，单点查询；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 50005
using namespace std;
int n, m, t;
long long a[MAXN], sum[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
			sum[i] += a[j];
		}
	}
}
void change(int l, int r, long long d) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		for (int i = l; i <= r; i++) a[i] += d;
		sum[p] += d * (r - l + 1);
	} else {
		for (int i = p + 1; i <= q - 1; i++) add[i] += d;
		for (int i = l; i <= R[p]; i++) a[i] += d;
		sum[p] += d * (R[p] - l + 1);
		for (int i = L[q]; i <= r; i++) a[i] += d;
		sum[q] += d * (r - L[q] + 1);
	}
}
long long query(int i) {
	return a[i] + add[pos[i]];
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r;
		long long d;
		scanf("%d %d %d %lld", &f, &l, &r, &d);
		if (f == 0) change(l, r, d);
		else printf("%lld\n", a[r] + add[pos[r]]);
	}
	return 0;
}

数列分块入门 2

题目

区间加法，查询区间内小于 x x x 的元素个数；

思路

由于要查询小于 x x x 的元素的个数，则，

对于散块的查询直接判断其大小即可；

对于整块的查询可以对块内进行从小到大排序，使得块内元素有序后使用二分 lower_bound 函数查找第一个大于等于 x x x 的元素，由于块内元素有序，所以其之前的元素均为小于 x x x 的，所以查询得到的下标减去所在块的左端点即为当前块内小于 x x x 的元素个数；

但注意，此时的整块内的标记还没有传递到元素上，所以在二分查找时，应查找块内第一个大于等于 x - add[i] 的元素下标；

由于整个块所有元素加同一个数，不会改变其有序性，所以只需在初始化以及修改零散元素后对其所在块进行重排即可；

由于询问的是原数组的下标，所以应该将原数组复制，用复制的数组进行排序；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 50005
using namespace std;
int n, m, t;
int a[MAXN], b[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN]; // b 为复制数组
void init(int n) {
	for (int i = 1; i <= n; i++) b[i] = a[i]; // 复制数列
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
		sort(b + L[i], 1 + b + R[i]); // 块内元素排序
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n, sort(b + L[t], 1 + b + R[t]);
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
		}
	}
}
void change(int l, int r, int d) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		for (int i = l; i <= r; i++) a[i] += d;
		for (int i = L[p]; i <= R[q]; i++) b[i] = a[i];
		sort(b + L[p], b + R[q] + 1); // 块内元素排序
	} else {
		for (int i = p + 1; i <= q - 1; i++) add[i] += d;
		for (int i = l; i <= R[p]; i++) a[i] += d;
		for (int i = L[p]; i <= R[p]; i++) b[i] = a[i];
		sort(b + L[p], 1 + b + R[p]); // 块内元素排序
		
		for (int i = L[q]; i <= r; i++) a[i] += d;
		for (int i = L[q]; i <= R[q]; i++) b[i] = a[i];
		sort(b + L[q], 1 + b + R[q]); // 块内元素排序
	}
}
int ask(int l, int r, int x) {
	int p = pos[l], q = pos[r];
	int ans = 0;
	if (p == q) {
		for (int i = l; i <= r; i++) ans += (x > (a[i] + add[p])); // 判断元素是否小于 x
	} else {
		for (int i = l; i <= R[p]; i++) ans += (x > (a[i] + add[p])); // 判断元素是否小于 x
		for (int i = L[q]; i <= r; i++) ans += (x > (a[i] + add[q])); // 判断元素是否小于 x
		for (int i = p + 1; i <= q - 1; i++) ans += lower_bound(b + L[i], b + R[i] + 1, x - add[i]) - b - L[i]; // 二分查找整块内小于 x 的个数
	}
	return ans;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r, d;
		scanf("%d %d %d %d", &f, &l, &r, &d);
		if (f == 0) change(l, r, d);
		else printf("%d\n", ask(l, r, d * d));
	}
	return 0;
}

数列分块入门 3

题目

区间加法，查询区间内小于 x x x 的最大值；

思路

大体思路同 数列分块入门 2 ，但查询时查询最大值；

即对于散块的查询直接判断其大小后更新答案即可；

对于整块的查询同样对块内元素进行从小到大排序，则使用二分 lower_bound 函数查找第一个大于等于 x x x 的元素，由于块内元素有序，所以查找元素的前一个元素即为当前块内小于 x x x 的最大值；

其余同 数列分块入门 2 ；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 100005
using namespace std;
int n;
int a[MAXN], b[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	for (int i = 1; i <= n; i++) b[i] = a[i];
	int t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
		sort(b + L[i], 1 + b + R[i]);
		
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n, sort(b + L[t], 1 + b + R[t]);
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
		}
	}
}
void change(int l, int r, int d) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		for (int i = l; i <= r; i++) a[i] += d;
		for (int i = L[p]; i <= R[q]; i++) b[i] = a[i];
		sort(b + L[p], b + R[q] + 1);
	} else {
		for (int i = p + 1; i <= q - 1; i++) add[i] += d;
		for (int i = l; i <= R[p]; i++) a[i] += d;
		for (int i = L[p]; i <= R[p]; i++) b[i] = a[i];
		sort(b + L[p], 1 + b + R[p]);
		
		for (int i = L[q]; i <= r; i++) a[i] += d;
		for (int i = L[q]; i <= R[q]; i++) b[i] = a[i];
		sort(b + L[q], 1 + b + R[q]);
	}
}
int ask(int l, int r, int w) {
	int p = pos[l], q = pos[r];
	int ans = -1;
	if (p == q) {
		for (int i = l; i <= r; i++) if (w > (a[i] + add[p])) ans = max(ans, a[i] + add[p]); // 判断是否小于 x 后更新答案
	} else {
		for (int i = l; i <= R[p]; i++) if (w > (a[i] + add[p])) ans = max(ans, a[i] + add[p]); // 判断是否小于 x 后更新答案
		for (int i = L[q]; i <= r; i++) if (w > (a[i] + add[q])) ans = max(ans, a[i] + add[q]); // 判断是否小于 x 后更新答案
		for (int i = p + 1; i <= q - 1; i++) {
			int pos = lower_bound(b + L[i], b + R[i] + 1, w - add[i]) - b - 1; // 寻找块内第一个大于等于 x 的元素的前一个元素
			if (w > (b[pos] + add[i])) ans = max(ans, b[pos] + add[i]);// 判断是否小于 x 后更新答案
		}
	}
	return ans;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r, d;
		scanf("%d %d %d %d", &f, &l, &r, &d);
		if (f == 0) change(l, r, d);
		else printf("%d\n", ask(l, r, d));
	}
	return 0;
}

数列分块入门 4

题目

区间加法，区间求和；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 50005
using namespace std;
int n, m, t;
long long a[MAXN], sum[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
			sum[i] += a[j];
		}
	}
}
void change(int l, int r, long long d) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		for (int i = l; i <= r; i++) a[i] += d;
		sum[p] += d * (r - l + 1);
	} else {
		for (int i = p + 1; i <= q - 1; i++) add[i] += d;
		for (int i = l; i <= R[p]; i++) a[i] += d;
		sum[p] += d * (R[p] - l + 1);
		for (int i = L[q]; i <= r; i++) a[i] += d;
		sum[q] += d * (r - L[q] + 1);
	}
}
long long ask(int l, int r) {
	int p = pos[l], q = pos[r];
	long long ans = 0;
	if (p == q) {
		for (int i = l; i <= r; i++) ans += a[i];
		ans += add[p] * (r - l + 1);
	} else {
		for (int i = p + 1; i <= q - 1; i++) ans += sum[i] + add[i] * (R[i] - L[i] + 1);
		for (int i = l; i <= R[p]; i++) ans += a[i];
		ans += add[p] * (R[p] - l + 1);
		for (int i = L[q]; i <= r; i++) ans += a[i];
		ans += add[q] * (r - L[q] + 1);
	}
	return ans;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r;
		long long d;
		scanf("%d %d %d %lld", &f, &l, &r, &d);
		if (f == 0) change(l, r, d);
		else printf("%lld\n", ask(l, r) % (d + 1));
	}
	return 0;
}

数列分块入门 5

题目

区间开方，区间求和；

思路

区间内元素开方，可先将元素值从其所属块中减去，开方，再加回其所属块的和之中；

则不再需要 a d d add add 标记；

对于零散元素直接修改即可，对于整块则只能对块内元素依次修改；

但若块内元素均为 1 ，即该块内元素无论如何开方均不变，则可用一个标记，判断该块内元素是否均为 1 ，若未被标记过才修改块内元素；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 50005
using namespace std;
int n, m;
int t, a[MAXN], sum[MAXN], L[MAXN], R[MAXN], pos[MAXN];
bool flag[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
			sum[i] += a[j];
		}
	}
}
void change(int l, int r, int d) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		for (int i = l; i <= r; i++) {
			sum[p] -= a[i]; // 块内区间和减去原值
			a[i] = sqrt(a[i]); // 元素开方
			sum[p] += a[i]; // 块内区间和加上开方后的值
		}
	} else {
		for (int i = l; i <= R[p]; i++) {
			sum[p] -= a[i]; // 块内区间和减去原值
			a[i] = sqrt(a[i]); // 元素开方
			sum[p] += a[i]; // 块内区间和加上开方后的值
		}
		for (int i = L[q]; i <= r; i++) {
			sum[q] -= a[i];// 块内区间和减去原值
			a[i] = sqrt(a[i]); // 元素开方
			sum[q] += a[i]; // 块内区间和加上开方后的值
		}
		for (int i = p + 1; i <= q - 1; i++) {
			if (!flag[i]) { // 块内元素可继续开方
				for (int j = L[i]; j <= R[i]; j++) {
					sum[i] -= a[j];// 块内区间和减去原值
					a[j] = sqrt(a[j]); // 元素开方
					sum[i] += a[j]; // 块内区间和加上开方后的值
				}
                if (sum[i] == R[i] - L[i] + 1) flag[i] = true; // 标记块内元素不可继续开方
			}
		}
	}
}
int ask(int l, int r) {
	int p = pos[l], q = pos[r];
	int ans = 0;
	if (p == q) {
		for (int i = l; i <= r; i++) ans += a[i];
	} else {
		for (int i = p + 1; i <= q - 1; i++) ans += sum[i];
		for (int i = l; i <= R[p]; i++) ans += a[i];
		for (int i = L[q]; i <= r; i++) ans += a[i];
	}
	return ans;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r, d;
		scanf("%d %d %d %d", &f, &l, &r, &d);
		if (f == 0) change(l, r, d);
		else printf("%d\n", ask(l, r));
	}
	return 0;
}

数列分块入门 6

题目

单点插入，单点询问；

思路

对于插入，为了方便可以将每一个块存入一个 vector 中，直接插入；

但当每 n \sqrt n n ​ 次插入后应该重新分块以防止块太大；

由于会重新分块，所以每次插入与查询时应用一个 while 循环找到查询下表当前所在的块以及块内编号，再查询或插入；

代码
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#include <algorithm>
#define MAXN 1000005
using namespace std;
int n, m, t;
int a[MAXN], sum[MAXN], add[MAXN], L[MAXN], R[MAXN], pos[MAXN];
vector <int> v[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) {
			pos[j] = i;
			v[i].push_back(a[j]); // 将块内元素存入 vector 中
		}
	}
	return;
}
void rebuild() { // 重新分块
	n = 0;
	for (int i = 1; i <= t; i++) {
		for (int j = 0; j < v[i].size(); j++) {
			a[++n] = v[i][j]; // 重构数列
		}
		v[i].clear();
	}
	init(n); // 初始化新数列
}
void change(int l, int r) { // l 前插入 r
	int i = 1;
	while (v[i].size() < l) l -= v[i++].size();
	v[i].insert(v[i].begin() + l - 1, r);
}
void query(int l) { // 单点询问
	int i = 1;
	while (v[i].size() < l) l -= v[i++].size();
	printf("%d\n", v[i][l - 1]);
	return;
}
int main() {
	scanf("%d", &n);
	int T = sqrt(2 * n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	init(n);
	int Q = n;
	while (Q--) {
		if (Q % T == 0) rebuild();
		int f, l, r, d;
		scanf("%d %d %d %d", &f, &l, &r, &d);
		if (f == 0) change(l, r);
		else query(r);
	}
	return 0;
}

数列分块入门 7

题目

区间乘法，区间加法，单点询问；

思路

由于同时区间修改两中操作，所以可使用两个 mul 与 add 分别标记块内的乘法与加法；

对于零散元素修改前，先将标记类似于线段树的懒惰标记向块内元素传递，再修改即可；

对于整块修改，则直接修改两个标记即可；

注意，乘法时加法与乘法标记均要修改；

代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 100005
#define MOD 10007
using namespace std;
int n, m, t;
long long a[MAXN], add[MAXN], mul[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		mul[i] = 1;
		for (int j = L[i]; j <= R[i]; j++) pos[j] = i;
	}
}
void down(int x) { // 向块内元素传递标记
	if (add[x] == 0 && mul[x] == 1) return;
	for (int i = L[x]; i <= R[x]; i++) a[i] = (a[i] * mul[x] % MOD + add[x]) % MOD;
	add[x] = 0, mul[x] = 1;
	return;
}
void cadd(int l, int r, long long d) { // 加法修改
	int p = pos[l], q = pos[r];
	if (p == q) {
		down(p);
		for (int i = l; i <= r; i++) a[i] = (a[i] + d) % MOD;
	} else {
		down(p);
		for (int i = l; i <= R[p]; i++) a[i] = (a[i] + d) % MOD;
		down(q);
		for (int i = L[q]; i <= r; i++) a[i] = (a[i] + d) % MOD;
		for (int i = p + 1; i <= q - 1; i++) add[i] = (add[i] + d) % MOD;
	}
}
void cmul(int l, int r, long long d) { // 乘法修改
	int p = pos[l], q = pos[r];
	if (p == q) {
		down(p);
		for (int i = l; i <= r; i++) a[i] = (a[i] * d) % MOD;
	} else {
		down(p);
		for (int i = l; i <= R[p]; i++) a[i] = (a[i] * d) % MOD;
		down(q);
		for (int i = L[q]; i <= r; i++) a[i] = (a[i] * d) % MOD;
		for (int i = p + 1; i <= q - 1; i++) {
			add[i] = (add[i] * d) % MOD;
			mul[i] = (mul[i] * d) % MOD;
		}
	}
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%lld", &a[i]), a[i] %= MOD;
	init(n);
	for (int i = 1; i <= n; i++) {
		int f, l, r;
		long long d;
		scanf("%d %d %d %lld", &f, &l, &r, &d);
		if (f == 0) cadd(l, r, d);
		else if (f == 1) cmul(l, r, d);
		else printf("%lld\n", (a[r] * mul[pos[r]] % MOD + add[pos[r]]) % MOD);
	}
	return 0;
}

数列分块入门 8

题目

区间询问等于 c c c 的元素个数，并修改区间的所有元素为 c c c ；

思路

由于区间修改为一个元素，则可设置一个标记 tag 维护一个块内所有的数是否相等，若全部等于 x x x ，则将数组标记为 x x x ，否则标记为 -1 ；

这样在处理整块的数组时，只有 tag == -1 时需要操作，对于不是整块的暴力即可；

对于零散元素修改前，先将标记类似于线段树的懒惰标记向块内元素传递，再统计，修改；在修改完后，还要更新标记；

对于整块元素，标记有 3 种情况，

  1. 若标记为 x x x 则说明当前块内元素均为 x x x ，答案直接加上块长即可；
  2. 若标记为 -1 则说明当前块内元素不同，则可直接修改标记，在向下传递时再更新元素；
  3. 否则则遍历块内元素依次统计，修改，再更新标记；
代码
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#define MAXN 100005
using namespace std;
int n, m, t;
int a[MAXN], tag[MAXN], L[MAXN], R[MAXN], pos[MAXN];
void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		tag[i] = a[L[i]];
		for (int j = L[i]; j <= R[i]; j++) {
			if (a[L[i]] != a[j]) tag[i] = -1;
			pos[j] = i;
		}
	}
}

void down(int x) { // 传递标记
	for (int i = L[x]; i <= R[x]; i++) a[i] = tag[x];
	return;
}
void update(int x) { // 更新标记
	tag[x] = -1;
	for (int i = L[x] + 1; i <= R[x]; i++) {
		if (a[L[x]] != a[i]) return;
	}
	tag[x] = a[L[x]];
}
int ask(int l, int r, int w) {
	int p = pos[l], q = pos[r];
	int ans = 0;
	if (p == q) {
		if (tag[p] != -1) down(p); // 传递标记
		for (int i = l; i <= r; i++) { // 统计并修改
			if (a[i] == w) ans++;
			else a[i] = w;
		}
		update(p); // 更新标记
	} else {
		if (tag[p] != -1) down(p); // 传递标记
		for (int i = l; i <= R[p]; i++) { // 统计并修改
			if (a[i] == w) ans++;
			else a[i] = w;
		}
		update(p); // 更新标记
		if (tag[q] != -1) down(q); // 传递标记
		for (int i = L[q]; i <= r; i++) { // 统计并修改
			if (a[i] == w) ans++;
			else a[i] = w;
		}
		update(q); // 更新标记
		for (int i = p + 1; i <= q - 1; i++) {
			if (tag[i] == w) ans += R[i] - L[i] + 1; // 情况 1
			else if (tag[i] != -1) tag[i] = w; // 情况 2
			else { // 情况 3
				for (int j = L[i]; j <= R[i]; j++) {
					if (a[j] == w) ans++;
					else a[j] = w;
				}
				update(i);
			}
		}
	}
	return ans;
}
int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	init(n);
	for (int i = 1; i <= n; i++) {
		int l, r, d;
		scanf("%d %d %d", &l, &r, &d);
		printf("%d\n", ask(l, r, d));
	}
	return 0;
}

数列分块入门 9

题目

询问区间的最小众数；

思路

由于询问区间的最小众数，

对于零散元素，则可直接统计；

对于整块，则可与处理出 d p [ i ] [ j ] dp[i][j] dp[i][j] 为块 i ∼ j i \sim j i∼j 的众数；

注意数据范围要离散化；

代码
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#include <algorithm>
#define MAXN 100005
#define MAXX 2005
using namespace std;
int n, m, t, L[MAXN], R[MAXN], pos[MAXN];
int a[MAXN], c[MAXN];
int s[MAXN], dp[MAXX][MAXX]; // 存储 i ~ j 号块众数
vector <int> p[MAXN]; // 储存当前元素是元素相同的第几个，以方便求区间内出现的次数 

void init(int n) {
	t = sqrt(n * 1.0);
	for (int i = 1; i <= t; i++) {
		L[i] = (i - 1) * t + 1;
		R[i] = i * t;
	}
	if (R[t] < n) t++, L[t] = R[t - 1] + 1, R[t] = n;
	for (int i = 1; i <= t; i++) {
		for (int j = L[i]; j <= R[i]; j++) pos[j] = i;
	}
    for (int i = 1; i <= n; i++) p[a[i]].push_back(i);
	for (int i = 1; i <= t; i++) {
		memset(s, 0, sizeof(s)); // 块内 j 出现次数
		int ans1 = 0, ans2 = 0;
		for (int j = L[i]; j <= n; j++){
			s[a[j]]++;
			if (s[a[j]] == ans2) ans1 = min(ans1, a[j]);
			if (s[a[j]] > ans2) ans1 = a[j], ans2 = s[a[j]];
			if (pos[j + 1] != pos[j]) dp[i][pos[j]] = ans1;
		}
	}
    return;
}

int count(int l, int r, int x) { // 获取块中 a[i] 数量
	return upper_bound(p[x].begin(), p[x].end(), r) - lower_bound(p[x].begin(), p[x].end(), l);
}
int query(int l, int r) {
	int p = pos[l], q = pos[r];
	if (p == q) {
		int ans1 = 0, ans2 = 0;
		for (int i = l; i <= r; i++){
			int t = count(l, r, a[i]);
			if (t > ans2) ans1 = a[i], ans2 = t;
			if (t == ans2) ans1 = min(ans1, a[i]);
		}
		return ans1;
	}
	int ans1 = dp[p + 1][q - 1]; // 在 p + 1 ~ q - 1 这一序列中的众数
    int ans2 = count(l, r, ans1); // 查找这个众数在区间里出现的个数 
	for (int i = l; i <= R[p]; i++) { // 暴力查找左边零散值每个数的数量 
		int t = count(l, r, a[i]);
		if (t == ans2) ans1 = min(ans1, a[i]);
		if (t > ans2) ans1 = a[i], ans2 = t;
	}
	
	for (int i = L[q]; i <= r; i++) { // 暴力查找右边零散值每个数的数量 
		int t = count(l, r, a[i]);
		if (t == ans2) ans1 = min(ans1, a[i]);
		if (t > ans2) ans1 = a[i], ans2 = t;
	}
	
	return ans1;
}

int main(){
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &a[i]); 
		c[i] = a[i];
	}
	sort(c + 1, c + n + 1);
	int l = unique(c + 1, c + n + 1) - c - 1;
	for (int i = 1; i <= n; i++) a[i] = lower_bound(c + 1, c + l + 1, a[i]) - c; // 离散化
    init(n);
	for (int i = 1; i <= n; i++) {
		int l, r;
		scanf("%d %d", &l, &r);
        if (l > r) swap(l, r);
		printf("%d\n", c[query(l, r)]);
	}
	return 0;
}
ZhuRanCheng
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
专题5-1 分块：数组分块
Wonderful_Day4z的博客
01-01 1135
专题5-1 分块：数组分块 PART 1 分块简介 对于分块，许多人可能不陌生，毕竟这是一个顾名思义的词语。 不过，作为一个教学贴，有必要和大家介绍一下分块的概念。 分块，顾名思义就是将要求的东西分成若干个部分，对于特定的区间进行特定的操作 线段树和分块有相似之处，我们来类比一下 可以看出，对于一个1-5的数组，我们把它分成若干部分，直到叶节点所代表的区间大小为1 综合时间空间复杂度考虑，我们每...
算法-数列分块入门 7（LibreOj-6283）.rar
09-16
《算法-数列分块入门 7（LibreOj-6283）》是针对计算机科学领域中的一种常用算法技巧——数列分块进行深入解析的教程。数列分块是一种优化线性结构查询的技术，常用于解决大规模数据处理问题，尤其是在动态维护和...
数列分块入门
R的博客
08-26 358
数列分块入门
数列分块(数据结构)学习笔记
weixin_30384031的博客
03-06 115
发现自己并没有掌握分块的正确姿势，然后于近期学习一下。 顺便提一下，分块是一个很好想，很暴力，复杂度较直接暴力比较低的算法 如果数据是随机数据那么实际复杂度会比期望要小。 然后最优分块的数目，根据不同的题目是不同的，可以通过均值不等式算出 但是大多数数据结构题目直接对数列进行$\sqrt{n}$的数列分块就可以了。 所以在下面的讨论中，我们假定所有数列分块按照最经典的$\sqr...
手写实现数组方法之分块、差集、删除数组某些元素和获取数组某些元素
浮生离梦的博客
08-22 4647
一、数组分块 数组分块，将数组拆分成多个 size 长度的区块，每个区块组成小数组，整体成一个二维数组。 数组分块的实现，代码如下所示： export function chunk (arr, size=1) { // 判断 if (arr.length === 0) { return []; } // 声明两个变量 let result = []; let tmp = []; // 遍历 arr.forEach(item => { // 判断 t
数据结构——分块：数列分块入门
Lunar Arc的博客
03-14 349
数据结构——分块：数列分块入门数列分块入门1题目算法分析Code数列分块入门4题目算法分析Code反思与总结 最近在学习分块，在这里分享一下联系的几道习题。 关于何为分块，请阅读 这篇文章 以下是分块的经典联系题。 LOJ：数列分块入门1-9 下面来分享最近完成的数列分块入门1和数列分块入门4。 数列分块入门1 题目 算法分析 详细见 数据结构——分块入门 Code #include<iostream> #include<cstdio> #include<algorithm&
算法-数列分块入门 8（LibreOj-6284）.rar
09-16
《算法-数列分块入门 8（LibreOj-6284）》是针对编程算法学习者的一份重要资源，主要讲解了数列分块这一算法思想及其在解决实际问题中的应用。数列分块作为一种优化数据结构和算法效率的方法，在处理大规模数据时尤...
算法-数列分块入门 2（LibreOj-6278）.rar
09-16
数列分块是一种在处理大规模数据时常用的优化技巧，尤其在算法竞赛和程序设计中有着广泛的应用。这个压缩包文件“算法-数列分块入门 2（LibreOj-6278）.rar”包含了一份关于数列分块的教程，可能是为了帮助学习者...
算法-数列分块入门 5（LibreOj-6281）.rar
09-16
数列分块是一种在处理大规模数据时常用的优化技巧，尤其在算法竞赛和高效编程中有着广泛的应用。这个压缩包文件“算法-数列分块入门 5（LibreOj-6281）.rar”包含了一份关于数列分块的详细教程，主要针对LibreOj上的...
算法-数列分块入门 1（LibreOj-6277）.rar
09-16
总结来说，数列分块是一种优化算法效率的重要技术，尤其适用于大数据处理和在线算法。掌握这项技能，能让你在面对复杂问题时有更多的解题思路，也能提升你在编程竞赛中的竞争力。通过阅读提供的PDF文档，你应该能够...
【原】javascript【数组分块】技术，从理解到熟练使用！
qq_38744335的博客
03-27 549
前面的话javascript是运行于单线程的环境中的，定时器仅仅只是计划代码在未来的某个时间执行。为什么要使用数组分块?我们经常见到这样的一段代码：for(var i=0,len=data.length;i&lt;len;i++){     //执行的代码 }data.length不大还好，当length达到成百上千甚至更大的时候，每次循环如果要50ms，那完成全部循环用时将是很恐怖的！前面说了j...
数列分块入门 (1 ~ 7)
lifehappy
07-20 343
分块 6277. 数列分块入门 1 分块思想 我们把每m个元素分成一块，所以我们总共的块数就是n/mn / mn/m块，一般情况下我们取m=nm = \sqrt{n}m=n​.对于区间加操作，我们可以先暴力左右两边，然后对于中间的整块的部分的加减，我们累加在块的标记上，然后我们每次查询的时候只要，每个元素的值加上这个块的标记值，就可以得到我们的答案了。 复杂度分析 每次操作我们修改的最多的元素最多就是O(n)O(\sqrt {n})O(n​)级别的个数，时间复杂读也就是O(n)O(\sqrt n)O(n​)
数列分块入门总结
mumei的博客
12-12 473
前序 分块是一种基于暴力的解决在线区间查询和区间修改等常见区间操作的算法，可以说是一种优雅的暴力，而且莫队等其他算法也是在这个算法的基础上进行的改进，所以说是很经典有用的技巧和思想。 知识 分块顾名思义就是把区间分成一块一块的处理，然后维护的是一个块里面的值，以达到快速解决题目给出的问题。这类算法思想不难理解，难的在于怎样运用，具体思想和代码实现可以参考UESTC的算法讲堂。 这个...
分块入门
Fire Dancer
05-25 461
Color the ballTime Limit: 9000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 19962 Accepted Submission(s): 9952Problem Description N个气球排成一排，从左到右依次编号为1,2,3
数组分块入门 3
SEIZE THE DAY
08-25 219
传送门 第一次用读入挂，感觉还行。 这题和数组分块2的题目差不多，只不过求的是最大前驱。 #include&lt;bits/stdc++.h&gt; using namespace std; const int maxn=100000+10; #define ll long long int a[maxn],belong[maxn],l[1005],r[1005],lazy[1005],...
数组分块1
SEIZE THE DAY
08-20 554
板子题 https://loj.ac/problem/6277 题目大意是 对于一个长度为n的数组进行区间操作和单点询问。  单点询问相对比较简单，数组简单存储之后就可以O(1)输出。  主要就是对于区间修改： 分块之后，对于需要修改的L~R的区间，可以简单分情况讨论： 1.L和R属于同一个块 2.L和R不属于同一个块 #include&lt;bits/stdc++.h&gt; u...
将一个数组按照固定大小进行拆分成数组
445822357
08-05 2118
/** * ArraySplit.java * Copyright(C) 2014 * creator:cuiran 2014-8-4 上午10:39:28 */ package com.udpdemo.test2; import java.util.ArrayList; import java.util.List; /** * * @author cuiran * @ver...
LOJ-6279-数列分块入门3(分块, 二分)
最新发布
05-24
题目描述 给定一个长度为n的序列a，有m次询问。每次询问给定l, r, k，要求区间[l, r]中第k小的数。 输入格式 第一行两个整数n,m。 接下来一行n个整数，表示序列a。 接下来m行，每行三个整数l,r,k。 输出格式 对于每个询问，输出一行一个数，表示区间[l, r]中第k小的数。 输入样例 5 3 1 3 2 4 5 1 5 2 2 4 1 3 5 3 输出样例 2 3 5 算法1 (分块) $O(n\sqrt n)$ 我们可以预处理出每一个块的信息，每个块又分为若干小块，每个小块中的数都小于等于块中的最大值，可以用二分查找确定小块中满足条件的数的个数，然后用根号分治处理。 时间复杂度 每次查询的时间复杂度是 $O(\sqrt n\log n)$ 的，总时间复杂度是 $O(n\sqrt n\log n)$ 的。 参考文献 算法竞赛进阶指南 C++ 代码 算法2 (二分答案) $O(n\log^2n)$ 我们二分答案，然后统计序列中小于等于这个答案的数的个数，统计方法可以用归并排序，在时间复杂度 $O(n\log n)$ 的时间内完成。 时间复杂度 每次查询的时间复杂度是 $O(n\log^2n)$ 的，总时间复杂度是 $O(mn\log^2n)$ 的。 参考文献 算法竞赛进阶指南 C++ 代码

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值